elektriskt fält

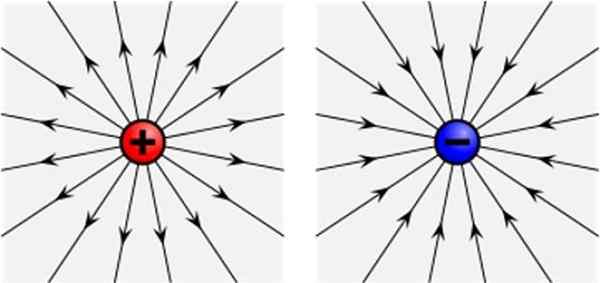
Det elektriska fältet för ett positivt (vänster) och negativt (höger). Källa: Wikimedia Commons

Vad är det elektriska fältet?

han elektriskt fält Det är egenskapen som föremålen laddade med att påverka det omgivande utrymmet har, vilket uppfattas av andra elektriskt laddade kroppar. Men till skillnad från den elektriska kraften mellan belastningar beror det elektriska fältet bara på lasten som producerar den.

Michael Faraday (1791-1867), en engelsk fysiker, skapade konceptet med fält genom att observera att all elektrisk laddning påverkar utrymmet som omger det, så att det inte behöver vara i kontakt med en annan belastning så att interaktionen inträffar.

Det är inte ens nödvändigt att belastningarna är i ett materiellt medium, eftersom interaktionen kan ges i ett vakuum.

För att visualisera formen på ett elektriskt fält, anta en specifik och positiv belastning, kallad +Q, vars storlek är så liten att det inte är nödvändigt att ta hänsyn till dess dimensioner. Fältet hon producerar kan påverka andra laddningar, till exempel en annan positiv testpunktbelastning Q_antingen.

Testbelastningen placeras på olika platser runt +Q, och för att vara båda positiva, kraften som +Q utövar på Q_antingen Det är avvisande.

Rita kraftkraften på lasten q_antingen Vid varje punkt i det utrymme det upptar och tar bort det finns det en uppsättning linjer som kommer radiellt från lasten +q (se bilden ovan, till vänster).

När du upprepar upplevelsen med en negativ belastning - Q är linjerna också radiella, men går in i - Q. I båda fallen är linjerna tangent till det elektriska elektriska fältet för lasten, utgående det när det är positivt och inkommande om det är negativt.

Formel och enheter

Om det finns ett elektriskt fält i ett elektriskt område OCH, En elektrisk laddning q_antingen Erfarenhet, tack till honom, en kraft som ges av:

Kan tjäna dig: slumpmässigt fel: formel och ekvationer, beräkning, exempel, övningar

F = Q_antingenOCH

Så att:

Den elektriska fältenheten i det internationella enhetssystemet är Newton/Coulomb, som förkortas N/C. Det är också vanligt att uttrycka det elektriska fältet i termer av en skalarstorlek som kallas elektrisk potential, i vilket fall fältet för fältet är volt/mätare (v/m).

Det elektriska fältet för en punktlig belastning

Fält OCH produceras av något objekt med belastning q. Att göra försöksbelastningen mycket liten, det vill säga att göra Q_antingen tenderar att 0, vektorn OCH är:

Med F_antingen Kraften mellan Q och Q_antingen.

Avsikten när man tar gränsen är att göra försöksbelastningen tillräckligt liten så att dess fält inte förändrar den som vill beräkna.

Om vad är en punktlig börda, enligt Coulombs lag, kraften mellan anklagelserna Q och Q_antingen, Båda separerade ett avstånd R, ges av:

I denna ekvation är K den elektrostatiska konstanten och enhetsvektorn i riktning mot linjen som förenar Q och Q och Q_antingen är:

Genom att ersätta detta uttryck i definitionen av fält erhålls det:

 Så att fältet OCH, Tillverkad av den punktliga belastningen Q vid punkt P, är:

Således, OCH Det beror inte på försöksbelastningen, men på belastningen som producerar den. De magnitud av fältet är direkt proportionellt mot lastens storlek och omvänt proportionell mot kvadratet på avståndet mellan lasten och punkten P.

Och som anges i början, adress Från fältet är det radiellt och riktningen är utgående till lasten när det är positivt och inkommande när det är negativt.

Elektrisk fältintensitet

Det elektriska fältet är vektor, och dess intensitet hänvisar till dess modul eller storlek, som betecknas utan djärv. För en punktlig belastning är intensiteten i dess elektriska fält helt enkelt:

Kan tjäna dig: ytlig utvidgning: formel, koefficienter och exempel

 Och för att vara modulen för ett belopp är det alltid positivt.

Till exempel intensiteten hos det elektriska fältet som produceras av en belastning Q = - 4.3 μC (μC läser “MicroCoulomb” och motsvarar miljonmi för en Coulomb), på ett avstånd av 2 cm från lasten, det är:

Observera att avståndet på 2 cm blev meter, multiplicerade med kraften 10⁻², Eftersom den elektrostatiska konstanten är i enheter om. Och även om lasten är negativ är intensiteten på det fält som det producerar alltid positiv, men den elektriska fältvektorn inkommer för lasten, som tidigare förklarats.

Electric Field Exempel

1. Elektriskt fält av en diskret fördelning av belastningar

En uppsättning specifika avgifter kallas Diskret belastningsfördelning. I så fall beräknas det resulterande elektriska fältet vid punkt P genom att tillämpa Superpositionsprincip, vilket är den summa vektorn i fältet som var och en av belastningarna producerar i P:

OCH_netto = OCH₁ + OCH₂ + OCH₃ +..

Följande bild visar en distribution som består av fem specifika belastningar och det elektriska fältet som var och en producerar vid punkt P:

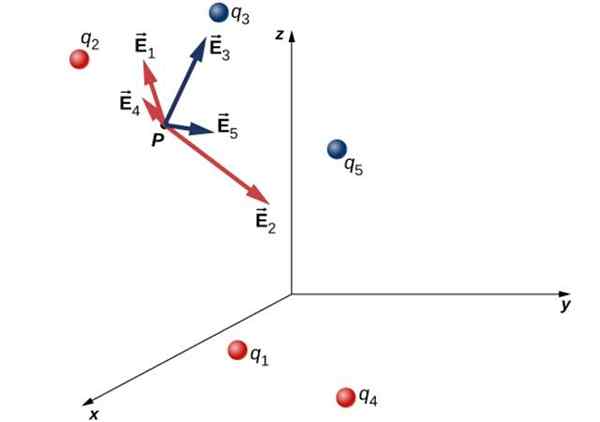Elektriskt fält vid punkt P, på grund av en diskret fördelning av belastningar

• Belastningarna q₃ och q₅ De är negativa och fältet de producerar inkommer för dem. De är utmärkta i blått.
• För sin del är belastningarna q₁, q₂ och q₄ De är positiva och skapar ett framstående fält i rött.

2. Elektriskt fält för en kontinuerlig fördelning av belastningar

En kontinuerlig belastningsfördelning består av ett utökat objekt, elektriskt laddad, till exempel den som visas i följande figur. Eftersom objektet har märkbara dimensioner är det fält som en del av kroppen producerar i P betydligt annorlunda än den som producerar ytterligare en (eller närmast) av P.

Kan tjäna dig: Kirchhoff -lagar

Anta att en liten elektrisk laddning av nämnda objekt tas, kallad DQ och antagen positiv, som producerar i ett litet bidrag till det totala elektriska fältet. Detta bidrag är en skillnad i den elektriska fältvektorn DOCH.

Eftersom DQ -belastningen är mycket liten är dess fält som en punktlig belastning, så ekvationen kan appliceras innan det ses:

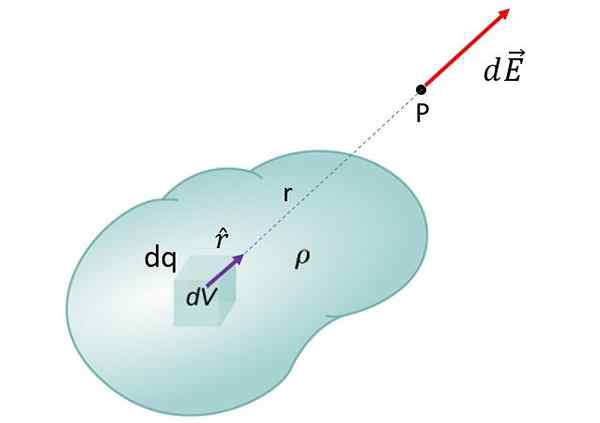För att beräkna det elektriska fältet för ett utökat objekt är det integrerat framför allt sin volym. Lastdensiteten (belastning per enhetsvolym) betecknas som ρ

För att få det totala fältet för objektet vid punkt P läggs bidrag från alla DQ som kan tas på objektet. Detta leder till integralen:

Träning löst

En punktlig belastning Q = 2.0 × 10⁻⁸ C placeras vid en punkt P inom ett elektriskt fält, där det upplever en stigande kraft av storleken 4.0 × 10⁻⁶ N. Beräkna:

a) Det elektriska fältet i P

b) kraften på en belastning q = −1.0 × 10⁻⁸ C Beläget i P.

Lösning till

Vara storleken på det elektriska fältet där lasten placeras. I kraft av detta fält upplever denna belastning den uppåtgående kraftkraften f, så att:

F = q ∙ e

Så:

E = f /q = 4.0 × 10^-6 N/ 2.0 × 10^-8 C = 200 n/c.

Att vara positiv bördan, kraften och fältet har samma riktning och betydelse.

Lösning B

Storleken på styrkan som verkar på vad som är:

När denna börda är negativ har kraft och fält samma riktning, men motsatta sinnen.

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 2. MC Graw Hill. 
2. Fält och elektrisk potential för en punktlig belastning. Hämtad från: SC.Ehu.är.
3. Resnick, r. (1999). Fysisk. Vul. 1. 3: e upplagan. på spanska. Kontinentala redaktionella företag s.TILL. av C.V.
4. Sears, Z. (2016). Universitetsfysik med modern fysik. 14th. Ed. Volym 1. Pearson.
5. Universitetsfysik. Elektriskt fält. Vul. 2. Hämtad från: OpenStax.org.