Brayton -cykelprocess, effektivitet, applikationer, övningar

han Brayton -cykel Det är en termodynamisk cykel som består av fyra processer och gäller en komprimerbar termodynamisk vätska som en gas. Hans första omnämnande är från slutet av 1700 -talet, även om han tillbringade lite tid innan han uppföddes av James Joule. Det är därför det också kallas Joule -cykeln.

Den består av följande steg, som bekvämt illustreras i tryckdiagrammet - volymen i figur 1: adiabatisk komprimering (ingen värme utbyts), isobarisk expansion (sker vid konstant tryck), adiabatisk expansion (ingen värme utbyts) och isobarisk komprimering (förekommer vid konstant tryck).

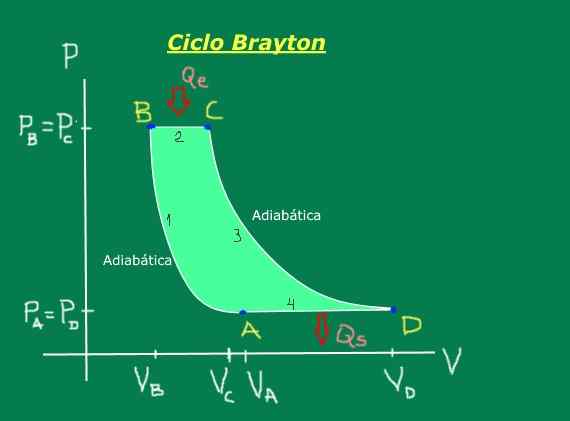Figur 1. Brayton -cykel. Källa: Självgjord.

[TOC]

Process och beskrivning

Brayton-cykeln är den perfekta termodynamiska cykeln som bäst appliceras för att förklara den termodynamiska funktionen av gasturbiner och blandar luftbränsle, som används för produktion av el och i flygmotorer.

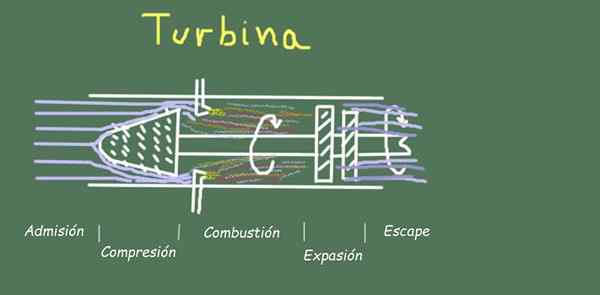figur 2. Turbinschema och flödessteg. Källa: Självgjord.

I drift av en turbin finns till exempel flera steg i flödet av operationgas, som vi kommer att se nedan.

Antagning

Den består av luftinloppet vid temperatur och miljötrycket på grund av turbinens öppning.

Kompression

Luften komprimeras av snurrande paletter mot andra som fixeras i avsnittet av turbinkompressorn. Denna komprimering är så snabb att det praktiskt taget inte finns någon värmeväxling, så den modelleras genom Brayton Cycle AB -processen. Luften vid kompressorns utgång har höjt sitt tryck och temperatur.

Förbränning

Luften är blandad med propangas eller pulveriserat bränsle som införs av injektorerna i förbränningskammaren. Blandningen producerar en kemisk förbränningsreaktion.

Denna reaktion är den som ger värmen som ökar temperaturen och kinetisk energi hos gaspartiklarna som expanderar i förbränningskammaren vid konstant tryck. I Brayton -cykeln modelleras detta steg med BC -processen som inträffar vid konstant tryck.

Expansion

I själva turbinen fortsätter luften att expandera mot turbinpaletterna och gör att den roterar och producerar mekaniskt arbete. I detta steg sänker luften temperaturen men utan att utbyta värme praktiskt med miljön.

I Brayton -cykeln simuleras detta steg som en adiabatisk expansionsprocess -CD. En del av turbinens arbete överförs till kompressorn och den andra används för att flytta en generator eller en propeller.

Uttömma

Den utgående luften är under konstant tryck lika med miljö och ger värme till den enorma massa av yttre luft, så på kort tid tar den samma inloppsluftstemperatur. I Brayton -cykeln simuleras detta steg med den ständiga tryckprocessen och stänger den termodynamiska cykeln.

Effektivitet baserad på temperatur, värme och tryck

Vi föreslår att du beräknar effektiviteten i Brayton -cykeln, för vilken vi börjar från definitionen av samma.

I en termisk maskin definieras effektiviteten som det nätarbete som utförts av maskinen dividerat med den tillhandahållna värmeenergin.

Det kan tjäna dig: lätt reflektion

Den första principen för termodynamik konstaterar att nettovärmen bidrog till en gas i en termodynamisk process är lika med variationen i den inre energin i gas plus det arbete som utförts av samma.

Men i en fullständig cykel är variationen av intern energi ogiltig, så den har att nettovärmen som bidragit i cykeln är lika med det gjorda nettoarbetet.

Inkommande värme, utgående värme och effektivitet

Det föregående uttrycket tillåter oss att skriva effektivitet baserat på absorberad eller inkommande värme (POSITVO) och värmen tilldelad eller utgående QS (negativ).

Värme och tryck i Brayton -cykeln

I Brayton -cykeln kommer värmen in i BC Isobaric -processen och kommer ut i den isobariska processen.

Antagande att icke av konstant tryck som levereras med känslig värme som i BC -processen, så ökar temperaturen från TB till TC enligt följande förhållande:

Var cp Det är värmekapaciteten vid konstant tryck.

Den utgående värmen QS Det kan beräknas på liknande sätt av följande förhållande som gäller för processen vid konstant tryck ger:

Att ersätta dessa uttryck i uttrycket som ger oss effektivitet baserat på inkommande värme och utgående värme, vilket gör de relevanta förenklingarna Följande relation för effektivitet erhålls:

Vilket resulterar i att effektiviteten är oberoende av luftmassan som passerar genom turbinen.

Förenklat resultat

Det är möjligt att förenkla det tidigare resultatet om vi tar hänsyn till det Pa = pd och? PB = PC Eftersom AD- och BC -processer är isobárica, det vill säga vid samma tryck.

Eftersom AB- och CD -processerna är adiabatiska uppfylls dessutom Poissons förhållande för båda processerna:

Var Gamma representerar den adiabatiska kvoten, det vill säga kvoten mellan värmekapaciteten vid konstant tryck och värmekapaciteten vid konstant volym.

Med hjälp av dessa förhållanden och förhållandet mellan tillståndsekvationen för en idealisk gas kan vi få ett alternativt uttryck för Poissons förhållande:

Som vi vet det Pa = pd och? PB = PC Ersätta och dela medlem till medlem, följande samband mellan temperaturer erhålls:

Om varje medlem av den föregående ekvationen dras från enheten, löses skillnaden och termerna är fixerade kan det demonstreras att:

Så att effektiviteten kan skrivas som en funktion av lufttemperatur vid inloppet och lufttemperaturen i slutet av kompressionsprocessen AB.

Prestanda beroende på tryckförhållandet

Uttrycket erhållet för effektiviteten i Brayton -cykeln baserat på temperaturer kan skrivas om att formuleras baserat på tryckförhållandet vid kompressorns utgång och ingång.

Detta uppnås om Poissons förhållande mellan punkter A och B är känt beroende på tryck och temperatur, vilket erhåller att cykelens effektivitet uttrycks enligt följande:

Det kan tjäna dig: relativt tryck: formel, hur det beräknas, exempel, träning

Att r kvoten mellan PB och PA.

Ett typiskt tryckförhållande är 8. I detta fall har Brayton -cykeln en teoretisk prestanda på 45%.

Ansökningar

Brayton -cykeln som en modell gäller gasturbiner som används i termoelektriska växter för att flytta generatorerna som producerar elektricitet.

Det är också en teoretisk modell som passar bra till driften av turboliska motorer som används i flygplan, men det är inte tillämpligt alls i flygplansturboreaktorer.

När det är intresserat.

Figur 3. Turbofan Motor effektivare än turboreactor. Källa: Pixabay

I flygplansturboreaktorer är det inte intresserat.

Tvärtom, det är intresserat.

Löst övningar

-Övning 1

En gasturbin som används i termoelektriska anläggningar har ett tryck vid 800 kPa -kompressoruttaget. Temperaturen på den inkommande gasen är miljön och är 25 Celsius, och trycket är 100 kPa.

I förbränningskammaren stiger temperaturen till 1027 Celsius för att komma in i turbinen.

Bestäm effektiviteten i cykeln, temperaturen på gasen ur kompressorn och gastemperaturen vid turbinuttaget.

Lösning

Eftersom vi har gastrycket vid kompressorns utgång och vi vet att ingångstrycket är atmosfärstryck, så det är möjligt att erhålla tryckförhållandet:

R = Pb / PA = 800 kPa / 100 kPa = 8

Eftersom gasen som turbinen arbetar är en blandning av propanluft och gas, appliceras sedan den adiabatiska koefficienten för en idealisk diatomisk gas, det vill säga en gammastill 1,4.

Effektiviteten skulle sedan beräknas så här:

Där vi har använt förhållandet som ger effektiviteten i Brayton -cykeln beroende på tryckförhållandet i kompressorn.

Temperaturberäkning

För att bestämma temperaturen vid kompressorns utgång, eller vad som är densamma den temperatur som gasen kommer in i förbränningskammaren, tillämpar vi relationsförhållandet med kompressorinmatningen och utgångstemperaturen.

Om vi ​​rensar TB -temperaturen från det uttrycket, får vi:

Med andra ord är temperaturen före komponentet 804.12 Celsius.

Som övning av övningen måste vi efter förbränning temperaturen stiger till 1027 Celsius för att komma in i turbinen. En del av gasens termiska energi används för att flytta turbinen, så temperaturen vid utgången måste vara lägre.

Kan tjäna dig: applikationer av energi, kraft, styrka, arbetskoncept

För att beräkna temperaturen vid turbinutgången kommer vi att använda ett förhållande mellan temperaturen tidigare:

Därifrån rensar vi TD för att få temperaturen vid turbinuttaget. Efter att ha utfört beräkningarna är den erhållna temperaturen:

TD = 143,05 Celsius.

-Övning 2

En gasturbin följer Brayton -cykeln. Trycket mellan kompressorns avgång och ingång är 12.

Anta omgivningstemperaturen på 300 K. Som ytterligare data är det känt att gastemperaturen efter förbränning (före ingången till turbinen) är 1000k.

Bestäm temperaturen vid kompressorns utgång och temperaturen vid turbinuttaget. Bestäm också hur många kilogram gas som cirkulerar genom turbinen i varje sekund, och vet att kraften är 30 kW.

Anta den specifika gasvärmen som konstant och ta värdet på det vid rumstemperatur: CP = 1 0035 J / (kg k).

Anta också att kompressionseffektiviteten i kompressorn och dekomprimering i turbinen är 100%, vilket är en idealisering eftersom förluster i praktiken alltid inträffar.

Lösning

För att bestämma temperaturen vid kompressorns utgång, känd temperaturen vid ingången, måste vi komma ihåg att det är en adiabatisk komprimering, så Poissons relation för AB -processen kan appliceras.

På detta sätt får vi att TB -temperaturen vid kompressorns utgång ges av:

På samma sätt är dekomprimeringen av gaserna som korsar turbinen en adiabatisk process som skulle motsvara Brayton -cykelprocessen. Därför kan vi tillämpa Poissons förhållande för att få turbinutloppstemperaturen.

För alla termodynamiska cykeler kommer nettoarbetet alltid att vara lika med nettovärmen som byts ut i cykeln.

I det tidigare förhållandet som är den inkommande (positiva) värmen och QS den utgående (negativa) värmen. I Brayton -cykeln inträffar dessa utbyten BC- och DA -processerna, båda isobáricas.

Nettoarbete per driftscykel kan sedan uttryckas beroende på gasmassan som cirkulerade i den cykeln och temperaturen.

I detta uttryck m Det är massan av gas som cirkulerade genom turbinen i en operationscykel och Cp Den specifika värmen.

Om vi ​​tar derivatet med avseende på tiden för det tidigare uttrycket, får vi netto -medelkraften baserat på massflödet.

Clearing m poäng, och ersätter temperaturen, kraften och värmekapaciteten för gas får vi ett massflöde på 1578,4 kg/s.

Referenser

1. Alfaro, j. Termodynamiska cykler. Återhämtat sig från: FIS.PUC.Kli.
2. Fernández J.F. Brayton -cykel. Gasturbin. ELLER.T.N. (Mendoza). Återhämtat sig från: edutecne.Utn.Edu.ar.
3. Sevilla universitet. Fysikavdelning. Brayton -cykel. Återhämtat sig från: Laplace.oss.är.
4. National Experimental University of the Táchira. Transportfenomen. Gaskraftscykler. Återhämtad från: unet.Edu.gå.
5. Wikipedia. Brayton -cykel. Återhämtat sig från: wikiwand.com
6. Wikipedia. Gasturbin. Återhämtat sig från: wikiwand.com.