Blandad elektrisk krets

Vi förklarar vad som är en blandad krets, dess egenskaper, delar, symboler och ger flera exempel

Vad är en blandad krets?

han blandad elektrisk krets Det är en som innehåller element som är anslutna både i serie och parallellt, så att när man stänger kretsen är olika spänningar och strömmar etablerade i var och en av dem.

Kretsarna är utformade med en mängd olika mål och deras element tillhör två kategorier: tillgångar och skulder.

De aktiva elementen i kretsen är generatorer eller spänning eller aktuella källor, direkt eller alternativa. Å andra sidan är de passiva elementen motståndet, kondensatorerna eller kondensatorerna och spolarna. Både en och andra medger anslutningar i serie och parallella, samt kombinationer av dessa.

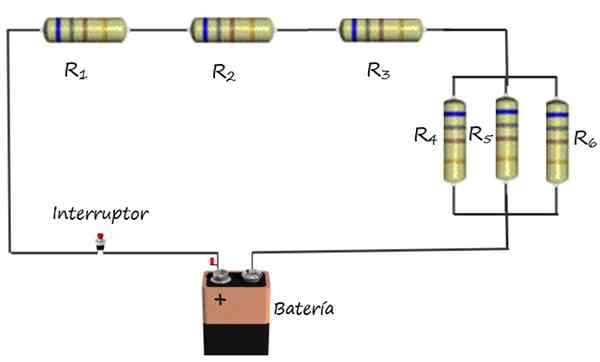
Den översta figuren visar som ett exempel en blandad förening av elektriska motstånd med ett batteri och en switch. Motstånd r₁, R₂ och r₃ De är associerade i serie, medan R -motstånd₄, R₅ och r₆ De är anslutna parallellt.

Andra möjliga anslutningar, skiljer sig från seriella parallella föreningar, är delta (eller triangel) och stjärna, som ofta används i elektriska maskiner som är matade med växlande ström.

Egenskaper hos en blandad krets

I allmänhet observeras följande i en blandad krets:

• Kretsmatning kan ske genom en direkt generator (batteri) eller alternativ.
• Det anses att kablarna eller ledningarna som förenar de olika elementen inte erbjuder strömmotstånd.
• Både spänning och ström kan vara konstant eller varierande i tid. Stora bokstäver används för att beteckna konstantvärden och små bokstäver när variabel.
• I rent resistiva blandade kretsar är strömmen genom seriemotstånd densamma, medan i parallella motstånd i allmänhet är det annorlunda. För att beräkna strömmen och spänningen genom varje motstånd reduceras kretsen vanligtvis till ett unikt motstånd, kallad ekvivalent motstånd eller r_eq .

Det kan tjäna dig: Vector Subtraktion: Grafisk metod, exempel, övningar

Serie motstånd

Motstånd i parallellt

• Om kretsen består av N -kondensatorer, när motsvarande kapacitans C är associerad i serie_eq resultat:

Seriekondensatorer

Parallellkondensatorer

• Spolarna eller induktorerna följer samma regler för förening som motstånd. Således, när du vill minska en serie spolförening för att få motsvarande induktans l_eq, Följande formler används:

Serieinduktorer

Induktorer i parallellt

• För att lösa de blandade kretsarna med motstånd används OHM -lagen och Kirchoff -lagarna. I enkla resistiva kretsar räcker Ohms lag, men för mer komplexa nätverk är det nödvändigt närvarande.

Förhållandet mellan spänning och ström

Beroende på kretselementet finns det ett samband mellan spänningen eller spänningen genom elementet med intensiteten hos strömmen som passerar genom det:

Motstånd R

Ohms lag används:

v_R(t) = R ∙ i_R(T)

Kondensator c

Induktans l

Delar av en blandad krets

I en elektrisk krets skiljer sig följande delar:

Knut

Unionspunkt mellan två eller flera ledande ledningar som ansluter vissa aktiva eller skulder i kretsen.

Gren

Element, vare sig de är aktiva eller skulder, som är mellan två på varandra följande knop.

Maska

Stängd del av kretsen som reste utan att passera två gånger genom samma punkt. Det kan eller inte har en spänning eller strömgenerator.

Kirchoff -lagar eller regler

Kirchoff -regler gäller både huruvida strömmar och spänningar är konstant eller om de är beroende av tid. Även om de vanligtvis kallas lagar, är de faktiskt regler för att tillämpa bevarandeprinciper på elektriska kretsar.

Kan tjäna dig: Solid State Physics: Egenskaper, struktur, exempel

Första regel

Det fastställer principen om bevarande av lasten och påpekar att summan av de nuvarande intensiteterna som kommer in i en knut, motsvarande summan av intensiteterna som kommer ut ur den:

∑ i_ingång = ∑ i_utgång

Andra regel

Vid detta tillfälle upprättas principen om energibesparing, när den säger att den algebraiska summan av spänningarna i en stängd del av kretsen (mesh) är noll.

∑ vi = 0

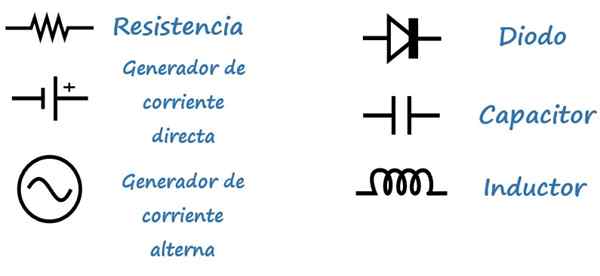
Symboler

För att underlätta analysen av kretsarna används följande symboler:

Exempel på blandade kretsar

Exempel 1

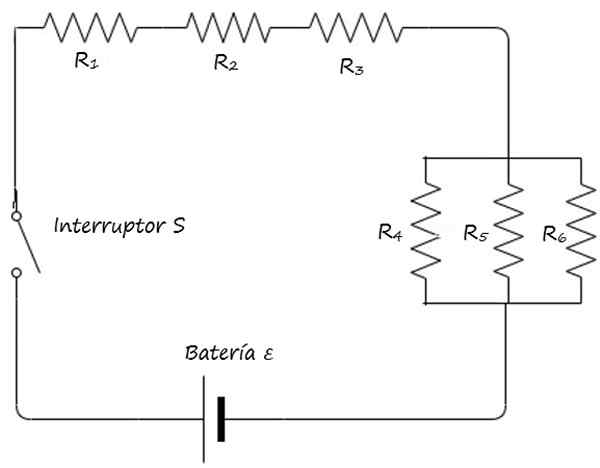
Rita den blandade kretsen i startfiguren kompakt genom att använda de symboler som beskrivs ovan.

Svar

Exempel 2

I kretsen i exempel 1 har du följande värden för motstånd och batteri:

R₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω, r₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω; ε = 100 V

För den visade kretsen anses batteriet vara idealiskt, det vill säga det har inget internt motstånd. Vanligtvis har riktiga batterier ett litet internt motstånd som ritas i serie med batteriet och behandlas på samma sätt som de andra motstånden i kretsen.

Beräkna följande:

• a) Kretsens motsvarande motstånd.
• b) värdet på strömmen som kommer ut ur batteriet.
• c) spänningar och strömmar i vart och ett av motståndet.

Svara på

Den första gruppen av motstånd: r₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω är anslutna i serie, därför är motsvarande motstånd R₁₂₃:

R₁₂₃ = R₁ + R₂ + R₃ = 50 Ω + 100 Ω + 75 Ω = 225 Ω

Det kan tjäna dig: Tredje lagen om termodynamik: formler, ekvationer, exempel

När det gäller R -motståndsgruppen₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω, är anslutna parallellt och motsvarande formel måste tillämpas:

 Det ömsesidiga eller omvända av det föregående resultatet är motsvarande motstånd för gruppen:

R₄₅₆ = 12 Ω

Den förenklade kretsen som erhålls visas i följande graf, bestående av två seriemotstånd med batteriet eller batteriet. Dessa två motstånd läggs till för att hitta motsvarande motstånd för den ursprungliga R -kretsen_eq:

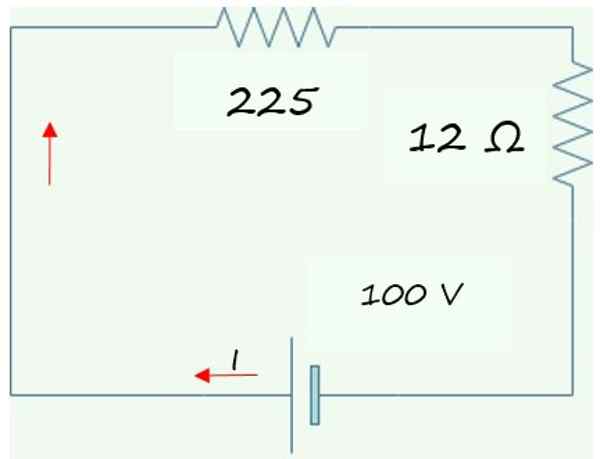
R_eq= 225 Ω + 12 Ω = 237 Ω

Svar B

Strömmen som lämnar batteriet (genom konvention ritas alltid av den positiva polen) beräknas med den förenklade kretsen, som består av motsvarande motstånd R_eq I serie med batteriet, till vilket Ohms lag tillämpas:

ε = i · r

I = ε / r = 100 v / 237 Ω = 0.422 a

Svar C

Spänningar och strömmar i var och en av SA -motstånd beräknar enligt Ohms lag. Det första som observeras är att strömmen som kommer ut ur batteriet korsar helt motståndet r₁ , R₂ och r₃ Och istället är det uppdelat genom att korsa r₄ , R₅ och r₆.

Spänningarna v₁, V₂ och v₃ är:

V₁  = 0.422 A × 50 Ω = 21.1 v
V₂  = 0.422 A × 100 Ω = 42.2 v
V₃  = 0.422 A × 75 Ω = 31.7 v

För sin del, VoltaJes V₄, V₅ och v₆ De har samma värde, eftersom motståndet är parallellt:

V₄ = V₅ = V₆ = 0.422 A × 12 Ω = 5.06 v

Och respektive strömmar är:

Yo₄ = 5.06 V / 24 Ω = 0.211 a

Yo₅ = Jag₆ = 5.06 V / 48 Ω = 0.105 a

Observera att genom att lägga till i₄, Yo₅ och jag₆ Den totala strömmen som kommer ut ur batteriet erhålls igen.