Klassificering av verkliga siffror

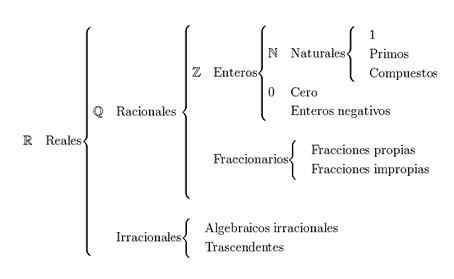
Den huvudsakliga Klassificering av verkliga siffror Det är uppdelat i naturliga siffror, hela siffror, rationella siffror och irrationella siffror. De verkliga siffrorna representeras med bokstaven r.

Verkliga siffror hänvisar till kombinationen av rationella och irrationella nummergrupper. För att bilda dessa grupper behövs naturliga siffror och hela siffror.

Det finns många sätt på vilka de olika verkliga siffrorna kan byggas eller beskrivas, varierande från enklare former till mer komplexa former, beroende på det matematiska arbetet som du vill utföra.

Hur klassificeras verkliga siffror?

- Naturliga siffror

Naturliga siffror representeras av bokstaven (n) och är de som används för att räkna (0,1,2,3,4 ...). Till exempel "det finns femton Rosas i trädgården ”,” Mexikos befolkning är från 126 miljoner av människor "eller" summan av två och två är fyra". Det bör noteras att vissa klassificeringar inkluderar 0 som ett naturligt antal och andra inte. 

Två barn som gör en summa av två naturliga siffror.

Naturliga siffror inkluderar inte de som har en decimaldel. Därför är ”Mexikos befolkning från 126.2 miljoner människor "eller" gör en temperatur på 24.5 Celsius grader ”naturliga nummer kunde inte övervägas.

På gemensamt språk, som grundskolor, kan naturliga nummer kallas redovisningsnummer för att utesluta negativa heltal och noll.

Naturliga siffror är de baser som många andra uppsättningar av siffror kan byggas i förlängning: hela siffror, rationella siffror, verkliga siffror och komplexa siffror, bland andra.

Egenskaperna för naturliga siffror, såsom delbarhet och distribution av primära nummer, studeras i antal teori. Problemen relaterade till räkning och beställning, såsom uppräkningar och partition, studeras i kombinatoriska.

De har flera egenskaper, såsom: summa, multiplikation, subtraktion, uppdelning, etc.

Kan tjäna dig: samtida vetenskap

Ordinära och kardinalnummer

Naturliga siffror kan vara ordinära eller kardinal.

Kardinalantal skulle vara de som används som naturliga nummer, som nämnts ovan i exemplen. "Ha två kakor "," Jag är far till tre barn "," Lådan inkluderar två presentkräm ". 

Ordinaler är de som uttrycker ordning eller anger en position. I ett lopp listas till exempel ankomsten av löparna av vinnaren och slutar den sista som kom till mållinjen.

På detta sätt kommer det att sägas att vinnaren är den "första", nästa "andra", nästa "tredje" och så vidare fram till det sista. Dessa siffror kan representeras av ett brev i deras övre höger för att förenkla skrivandet (1: a, 2: a, 3: e, 4: e, etc.).

- Heltal

Hela siffrorna består av de naturliga siffrorna och deras motsatser, det vill säga de negativa siffrorna (0, 1, -1, 2, -2, 50, -50 ...). Liksom naturliga siffror inkluderar dessa inte de som har en decimaldel.

Exempel på hela siffror skulle vara "genomsnitt 30: e i Tyskland", "Jag stannade klockan 0 när jag nådde slutet av månaden", "För att gå ner till källaren måste du markera hissens hiss".

I sin tur kan inte hela siffror skrivas med en fraktionerad komponent. Till exempel siffror som 8.58 eller √2 är inte hela siffror.

Hela siffror representeras med bokstaven (z). Z är en undermailgrupp med rationella nummer Q, som i sin tur utgör gruppen av verkliga n -nummer. Liksom naturliga siffror är Z en oändlig redovisningsgrupp.

Heltal bildar den minsta gruppen och den minsta uppsättningen naturliga siffror. I algebraiska siffror teori kallas hela siffror ibland irrationella för att skilja dem från algebraiska heltal.

Det kan tjäna dig: Forskningsprojekt: Fester, hur det utarbetas och exempel

- Rationella nummer

Uppsättningen av rationella nummer representeras av bokstaven (Q) och inkluderar alla de nummer som kan skrivas som en bråkdel av hela siffror.

Det vill säga denna uppsättning inkluderar naturliga nummer (4/1), hela siffror (-4/1) och exakta decimalantal (15,50 = 1550/100).

Distributionen av 1/6 av ost är ett rationellt antal.

Decimalutvidgningen av ett rationellt antal slutar alltid efter att ett begränsat antal siffror (t.ex. 15.50) eller när samma ändliga sekvens av siffror börjar upprepas om och om igen (t.ex. 0.345666666666666 ...). Därför ingår siffrorna inom uppsättningen av rationella siffror. rena tidningar eller blandade tidningar.

Dessutom representerar alla upprepade eller terminala decimaler ett rationellt antal. Dessa uttalanden gäller inte bara för bas 10, utan också för något annat basnummer.

Ett riktigt nummer som inte är rationellt kallas irrationellt. Irrationella siffror inkluderar till exempel π och E. Eftersom hela uppsättningen av rationella siffror är domberbar och att gruppen med verkliga siffror inte är bedövningsbar kan det sägas att nästan alla verkliga siffror är irrationella.

Rationella siffror kan formellt definieras som ekvivalensklasser av hela par (P, Q) så att Q ≠ 0 eller motsvarande förhållande definieras av (P1, Q1) (P2, Q2) endast om P1, Q2 = P2Q1.

De rationella siffrorna, tillsammans med summan och multiplikation, formfält som utgör hela siffrorna och finns i alla grenar som innehåller hela.

- Irrationella siffror

Irrationella siffror är alla verkliga siffror som inte är rationella siffror; Irrationella siffror kan inte uttryckas som fraktioner. De rationella siffrorna är siffrorna som består av fraktioner av hela siffror.

Som en följd av sångartestet som säger att alla verkliga siffror inte är otaliga och att de rationella om de är siffror kan dras slutsatsen att nästan alla verkliga siffror är irrationella.

Kan tjäna dig: bana och förskjutning

När radien för två linjesegment är ett irrationellt antal kan det sägas att dessa linjesegment är oändliga; vilket innebär att det inte finns en tillräcklig längd så att var och en av dem kan vara "mått" med ett flera speciellt heltal av samma.

Bland de irrationella siffrorna är radien π för en cirkelcirkel till dess diameter, antalet Euler (E), det gyllene numret (φ) och kvadratroten på två; Ännu mer är alla fyrkantiga rötter av naturliga siffror irrationella. Det enda undantaget från denna regel är de perfekta rutorna.

Det kan observeras att när irrationella siffror uttrycks positionerat i ett siffersystem, (som decimalnummer) inte slutar eller upprepas.

Detta innebär att de inte innehåller en sekvens av siffror, upprepningen genom vilken en rad representation görs.

Förenkling av det irrationella antalet PI.

Till exempel: decimalrepresentationen av antalet π börjar med 3.14159265358979, men det finns inget ändligt antal siffror som kan representera π exakt och kan inte heller upprepas.

Beviset på att decimalutvidgningen av ett rationellt antal måste avsluta eller upprepa skiljer sig från beviset på att en decimalförlängning måste vara ett rationellt antal; Även om de är grundläggande och något långa, tar dessa tester lite arbete.

Vanligtvis tar matematiker i allmänhet inte uppfattningen om att "avsluta eller upprepa" för att definiera begreppet ett rationellt antal.

Irrationella siffror kan också behandlas via icke -kontinuerliga fraktioner.

Referenser

1. Klassificera riktiga siffror. Återhämtat sig från chilimat.com.
2. Naturligt nummer. Återhämtat sig från Wikipedia.org.
3. Antal klassificering. Dituutor återhämtade sig.com.
4. Återhämtat sig från Wikipedia.org.
5. Irrationellt tal. Återhämtat sig från Wikipedia.org.