Kongruens kongruenta siffror, kriterier, exempel, övningar
- 3507
- 857
- PhD. Lennart Johansson
De kongruens, I geometri påpekar han att om två platta siffror har samma form och dimensioner är dessa kongruenta. Till exempel är två segment kongruenta när deras längder är lika. Även de kongruenta vinklarna har samma mått, även om de inte är orienterade på samma sätt i planet.
Termen "kongruens" kommer från latin Kongresen, vars betydelse är korrespondens. Således motsvarar två kongruenta figurer exakt en med den andra.
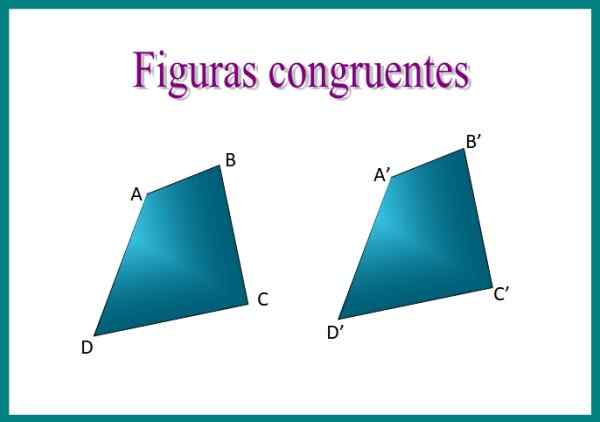
Figur 1. Kvadrilateralerna ABCD och A'B'C'd 'av figuren är kongruenta: deras sidor har samma mått, liksom deras inre vinklar. Källa: f. Zapata. Om vi till exempel överlappar de två fyrkantiga bildarna kommer vi att upptäcka att de är kongruenta, eftersom dispositionen av deras sidor är identisk och de mäter samma.
När du placerar kvadrilateralerna ABCD och A'B'C'D 'en på den andra, kommer siffrorna att sammanfalla exakt. Matchande sidor kallas homologa sidor antingen motsvarande Och för att uttrycka kongruens används symbolen ≡. Då kan vi säga att ABCD ≡ A'B'C'D '.
[TOC]
Kongruenskriterier
Följande egenskaper är vanliga för kongruenta polygoner:
-Lika form och storlek.
-Identiska mått på dina vinklar.
-Samma utsträckning på var och en av dess sidor.
I händelse av att två polygoner i fråga är regelbundna, det vill säga att alla sidor och inre vinklar mäter samma sak, är kongruensen säker på när ett av följande villkor är uppfyllda:
-Sidorna är kongruenta
-De apotem har samma åtgärd
-han radio av varje polygon mäter samma
Apotemet för en vanlig polygon är avståndet mellan mitten och en av sidorna, medan radien motsvarar avståndet mellan mitten och ett toppunkt eller en hörn av figuren.
Kongruenskriterier används ofta eftersom många delar och delar av alla slag tillverkas i serie och måste ha samma form och åtgärder. På detta sätt kan de enkelt bytas ut vid behov, till exempel muttrar, skruvar, ark eller kullersten på marken på gatan.
Kan tjäna dig: Simpson regel: formel, demonstration, exempel, övningar
figur 2. Street Cobblestones är kongruenta figurer, eftersom deras form och dimensioner är exakt desamma, även om deras orientering på golvet kan förändras. Källa: Pixabay. Kongruens, identitet och likhet
Det finns till exempel geometriska begrepp relaterade till kongruens De identiska figurerna och den Liknande siffror, som inte nödvändigtvis innebär att siffrorna är kongruenta.
Observera att de kongruenta figurerna är identiska, men fyrkanten i figur 1 kan vara orienterade på olika sätt på planet och fortfarande fortsätter att vara kongruent, eftersom den olika orienteringen inte ändrar storleken på deras sidor eller deras vinklar. I det här fallet skulle de upphöra att vara identiska.
Det andra konceptet är att likheten mellan figurerna: två platta figurer är liknande om de har samma form och deras inre vinklar mäter samma, även om storleken på figurerna kan vara annorlunda. Om detta är fallet är siffrorna inte kongruenta.
Kongruensexempel
- Vinklar kongruens
Som vi indikerade i början har de kongruenta vinklarna samma mått. Det finns flera sätt att få kongruenta vinklar:
Exempel 1
Två rader med en gemensam punkt definierar två vinklar, kallade Motsatta vinklar av toppunkten. Dessa vinklar har samma mått, därför är de kongruenta.
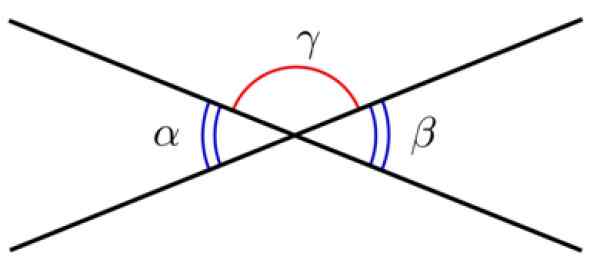Figur 3. Motsatta vinklar av toppunkten. Källa: Wikimedia Commons. Exempel 2
Det finns två parallella linjer plus en linje t Det korsar dem båda. Liksom i föregående exempel, när denna linje korsar parallellerna genererar den kongruenta vinklar, en på varje linje till höger sida och två andra på vänster sida. Figuren visar a och a1, till höger om linjen t, De är kongruenta.
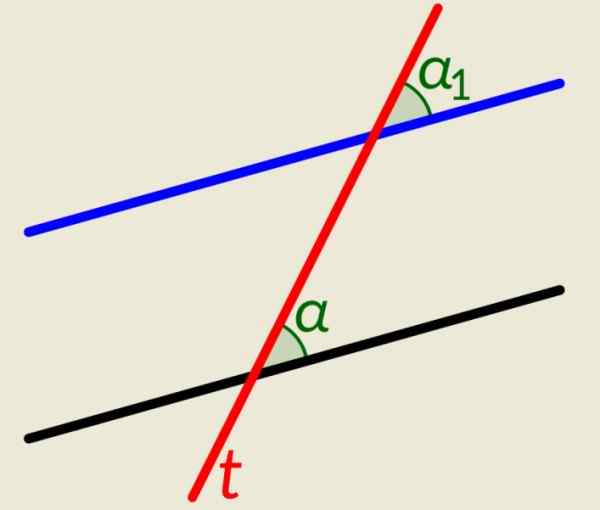Figur 4. Vinklarna som visas i figuren är kongruenta. Källa: Wikimedia Commons. LFAHLBERG/CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/3.0). Exempel 3
I ett parallellogram finns det fyra inre vinklar, som är kongruenta två till två. De är de mellan motsatta vertikaler, som visas i följande figur, där de två gröna vinklarna är kongruenta, liksom de två vinklarna i rött.
Kan tjäna dig: acutangle triangel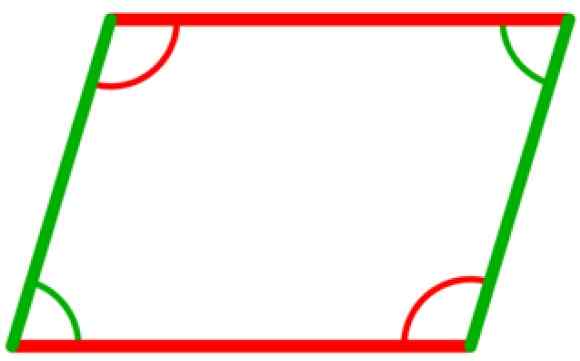
Figur 5. De inre vinklarna i parallellogrammet är kongruenta två till två. Källa: Wikimedia Commons. - Trianglar
Två trianglar med identisk form och samma storlek är kongruenta. För att verifiera detta finns det tre kriterier som kan undersökas på jakt efter kongruens:
-LLL -kriterier: De tre sidorna av trianglarna har samma åtgärder, därför l1 = L '1; L2 = L '2 och jag3 = L '3.
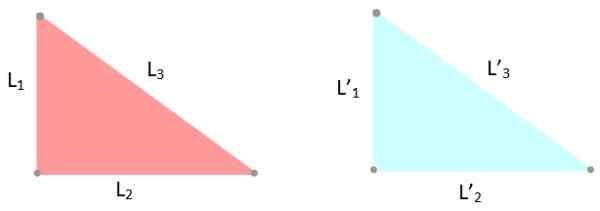Figur 6. Exempel på kongruenta trianglar, vars sidor mäter samma. Källa: f. Zapata. -Kriterier alla y aal: Trianglarna har två lika inre vinklar och sidan mellan dessa vinklar har samma mått.
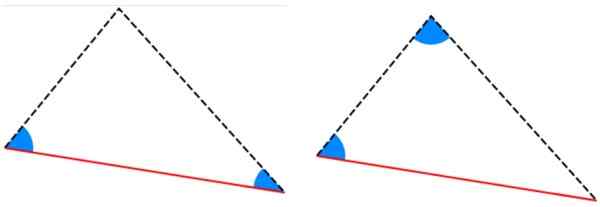Figur 7. Kriterier ala och aal för kongruens av trianglar. Källa: Wikimedia Commons. -Lalkriterier: Två av sidorna är identiska (motsvarande) och bland dem finns det samma vinkel.
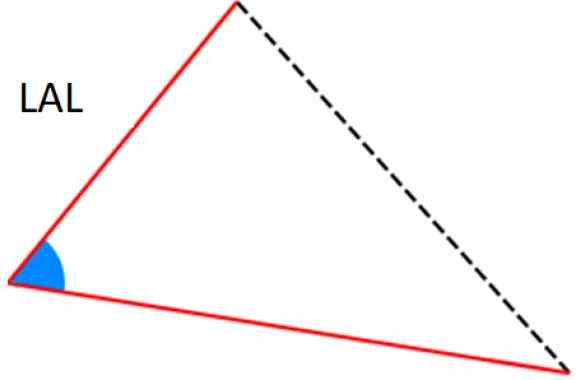Figur 8. Lal kriterier för kongruens av trianglar. Källa: Wikimedia Commons. Löst övningar
- Övning 1
I följande figur visas två trianglar: ΔABC och ΔECF. Det är känt att ac = ef, att ab = 6 och att cf = 10. Dessutom är vinklarna ∡bac och ∡FEC kongruenta och vinklarna ∡acb och ∡fcb är också.
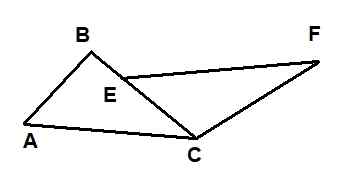Figur 9. Trianglar för exemplet löst 1. Källa: f. Zapata. Då är längden på BE -segmentet lika med:
(i) 5
(Ii) 3
(Iii) 4
(Iv) 2
(v) 6
Lösning
Eftersom de två trianglarna har ena sidan av lika längd AC = EF mellan lika vinklarna ∡bac = ∡cef och ∡bca = ∡cfe kan det sägas att de två trianglarna är kongruenta av kriterierna vinge.
Det är ΔBAC ≡ ΔCEF, så du måste:
BA = CE = AB = 6
BC = CF = 10
Ac = ef
Men det segment du vill beräkna är att vara = BC - EC = 10 - 6 = 4.
Så att rätt svar är (iii).
- Övning 2
Tre trianglar visas i figuren. Det är också känt att de två indikerade vinklarna mäter 80º vardera och att segmenten AB = PD och AP = CD. Hitta värdet på vinkel X som anges i figuren.
Det kan tjäna dig: polybal grafik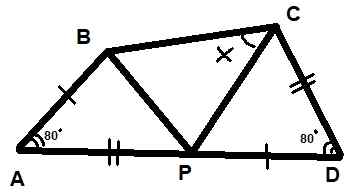
Figur 10. Trianglar för exemplet löst 2. Källa: f. Zapata. Lösning
Du måste tillämpa egenskaperna hos trianglarna, som är detaljerade steg för steg.
Steg 1
Från och med kriterierna för kongruens av Lal Triangles kan det sägas att BAP- och PDC -trianglarna är kongruenta:
ΔBAP ≡ ΔPDC
Steg 2
Ovanstående leder till att bekräfta att BP = PC, därför är triangeln ΔBPC isosceles och ∡pcb = ∡pbc = x.
Steg 3
Om vi kallar γ i BPC -vinkeln följer det att:
2x + y = 180º
Steg 4
Och om vi kallar ß till APB- och DCP- och a -vinklarna mot ABP- och DPC -vinklarna, måste det:
α + β + y = 180º (eftersom APB är en platt vinkel).
Steg 5
Dessutom är a + β + 80º = 180º med summan av inre vinklar i APB -triangeln.
Steg 6
Genom att kombinera alla dessa uttryck måste du:
α + β = 100º
Steg 7
Och därför:
y = 80º.
Steg 8
Slutligen följer det:
2x + 80º = 180º
Med x = 50º.
Referenser
- Baldor, a. 1973.Platt och rymdgeometri. Centralamerikansk kultur.
- CK-12 Foundation. Kongruenta polygoner. Hämtad från: CK 12.org.
- Njut av matematik. Definitioner: Radio (polygon). Återhämtat sig från: njutmatimaticas.com.
- Matematik öppen referens. Testa polygoner för kongruens. Återhämtat sig från: MathPenref.com.
- Wikipedia. Kongruens (geometri). Återhämtad från: är.Wikipedia.org.
- Zapata, f. Trianglar, historia, element, klassificering, egenskaper. Hämtad från: Lifer.com.