FÖRSTA KLAY Ekvationer Formel, hur man löser dem, exempel, övningar
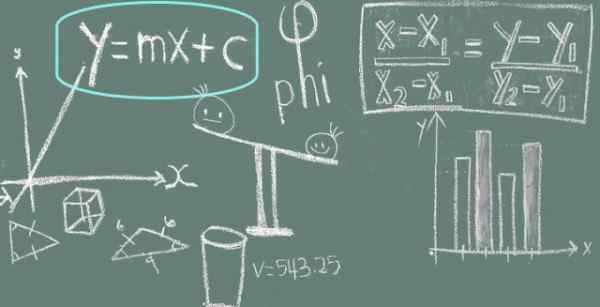
- 2663
- 126
- PhD. Emil Svensson
De Första graden eller linjära ekvationer Med en okänd är de som kan uttryckas som summan av två termer, på följande sätt:
yxa + b = 0
Var A och B, med till ≠ 0, är verkliga siffror r eller också komplex c. För att lösa det transponeras termer, vilket innebär att ändra termer från en sida till en annan av jämlikhet.
 Figur 1. En linjär ekvation är y = mx + c -form med y = 0. Källa: Pxhere.
Figur 1. En linjär ekvation är y = mx + c -form med y = 0. Källa: Pxhere. För att rensa det okända transponeras termen +B, som måste gå till höger om jämlikhet med ett förändrat tecken.
yxa = -b
Sedan rensas värdet på X på detta sätt:
x = - b/a
Som ett exempel kommer vi att lösa följande ekvation:
6x - 5 = 4
Vi transponerar termen -5 till höger med ett ändrat tecken:
6x = 4 + 5
Detta motsvarar att lägga till 5 på båda sidor av den ursprungliga ekvationen:
6x - 5 + 5 = 4 + 5 → 6x = 9
Och nu rensar vi det okända "X":
x = 9/6 = 3/2
Vilket motsvarar att dela båda sidor av jämlikhet med 6. Så vi kan bedöma följande för att få lösningen:
-Samma mängd kan läggas till eller subtraheras båda sidor av jämlikhet i en ekvation utan att förändra den.
-Du kan också multiplicera (eller dela) med samma mängd till alla termer både till vänster och till höger om ekvationen.
-Och om båda medlemmarna i en ekvation stiger till samma makt, ändras inte heller jämlikhet.
[TOC]
Hur man löser första gradsekvationer
Lösningen av en första gradsekvation kallas också roten till samma. Det är värdet på X som konverterar det ursprungliga uttrycket till en jämlikhet. Till exempel i:
5x = 8x - 15
Om vi ersätter x = 5 i denna ekvation erhålls den:
5⋅5 = 8⋅5 - 15
25 = 40 - 15
25 = 25
Eftersom den första graden linjära ekvationer kommer på många sätt, som ibland inte är uppenbara, finns det en serie allmänna regler som utgör flera algebraiska manipulationer för att hitta värdet på det okända:
-Först, om det anges, måste dessa genomföras.
-Grupperingssymboler som parenteser, fyrkantiga parenteser och nycklar, om de finns, måste undertryckas genom att bibehålla lämpliga tecken.
-Villkoren transponeras för att placera alla de som innehåller det okända för en enda sida av jämlikhet, och de som inte innehåller det till den andra.
-Sedan reduceras alla liknande termer för att nå formen yxa = -b.
-Och det sista steget är att rensa det okända.
Grafisk tolkning
Den första gradsekvationen som höjs i början kan härledas från ekvationen för linjen y = mx+c, gör y = 0. Värdet på X som resultat motsvarar skärningspunkten mellan linjen med den horisontella axeln.
I följande figur har du tre rader. Börjar med den gröna linjen, vars ekvation är:
Kan tjäna dig: faktoriseringy = 2x - 6
Att göra y = 0 i linjen i linjen erhålls den första gradsekvationen:
2x - 6 = 0
Vars lösning är x = 6/2 = 3. Nu när vi beskriver grafen är det lätt att inse att linjen i själva verket skär till den horisontella axeln vid x = 3.
Den blå linjen korsar X -axeln vid x = 5, vilket är lösningen på ekvationen -x + 5 = 0. Slutligen, linjen vars ekvation är y = 0.5x + 2 skär till x -axeln vid x = -4, som lätt varnas för första gradsekvationen:
0.5 x + 2 = 0
x = 2/0.5 = 4
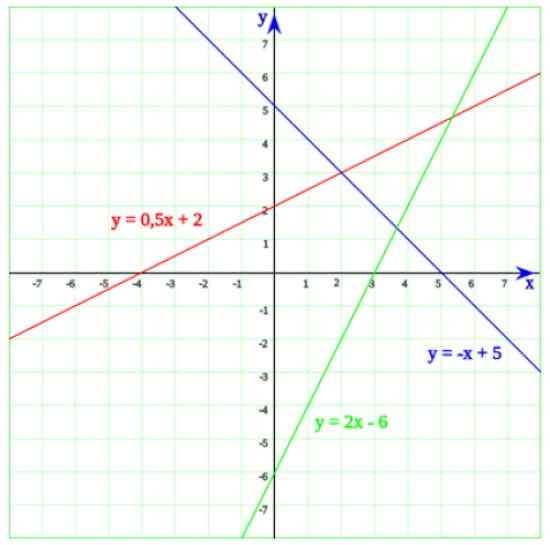 figur 2. Tre linjer vars korsningar med den horisontella axeln motsvarar linjära ekvationer. Källa: Wikimedia Commons.
figur 2. Tre linjer vars korsningar med den horisontella axeln motsvarar linjära ekvationer. Källa: Wikimedia Commons. Exempel på enkla linjära ekvationer
Hela ekvationerna
De är de i vars termer Det finns inga nämnare, till exempel:
21 - 6x = 27 - 8x
Dess lösning är:
-6x + 8x = 27 - 21
2x = 6
x = 3
Bråkekvationer
Dessa ekvationer innehåller minst en annan nämnare på 1. För att lösa dem är det tillrådligt.
Följande ekvation är fraktionerad typ:

Eftersom dessa siffror är små är det inte svårt att se att m.c.M (6, 8,12) = 24. Detta resultat erhålls lätt genom att uttrycka siffror som en produkt av primtal eller deras krafter, låt oss se:
6 = 3.2
8 = 23
12 = 22⋅3
Den minsta gemensamma multipeln bestäms genom att multiplicera de vanliga och icke -vanliga faktorerna på 6, 8 och 12 med dess största exponent, då:
MCM (6,8,12) = 23 ⋅3 = 8 × 3 = 24
Eftersom den minsta gemensamma multipeln är tillgänglig måste den multipliceras med var och en av villkoren för ekvationen:
-24\left&space;(\frac2x+38&space;\right&space;)=24\left&space;(\frac1-5x12&space;\right&space;))
4 (x+5) -3 (2x+3) = 2 (1-5x)
Vi använder sig av distribuerande egendom:
4x + 20 - 6x -9 = 2 - 10x
Alla termer som innehåller det okända "X" är grupperade till vänster om jämlikhet och lämnar de oberoende eller numeriska termerna på höger sida:
4x - 6x + 10 x = 2 +9 - 20
8x = -9
x = - 9/8
Bokstavliga ekvationer
De är linjära ekvationer med en okänd, som dock åtföljs av bokstavliga koefficienter (bokstäver). Dessa brev behandlas precis som det skulle göras med siffrorna. Ett exempel på en bokstavlig första gradsekvation är:
-3ax + 2a = 5x - b
Denna ekvation löses på samma sätt som om de oberoende termerna och koefficienterna var numeriska:
-3ax - 5x = - b - 2a
Faktorera det okända "x":
x (-3a - 5) = - b - 2a
x = ( - b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)
Första gradsekvationer
Ekvationssystem består av en uppsättning ekvationer med två eller flera okända. Systemlösningen består av värden som uppfyller ekvationerna samtidigt och för att bestämma den otvetydigt måste det finnas en ekvation för varje okända.
Kan tjäna dig: vektoralgebraDen allmänna formen av ett system av m Linjära ekvationer med n Okända är:
tillelvax1 + till12x2 +Till ... till1nxn = B1
tilltjugoettx1 + till22x2 +Till ... till2nxn = B2
..
tillM1x1 + tillm2x2 +Till ... tillmnxn = Bm
Om systemet har en lösning sägs det att det är bestämd kompatibel, När det finns en oändlig uppsättning värden som tillfredsställer det är det obestämd kompatibel, Och slutligen, om det inte har någon lösning, är den oförenlig.
I upplösningen av linjära ekvationssystem används flera metoder: reduktion, ersättning, utjämning, grafiska metoder, Gauss-Jordan eliminering och användning av determinanter är bland de mest använda. Men det finns andra algoritmer för att nå lösningen, bekvämare för system med många ekvationer och okända.
Ett exempel på ett system med linjära ekvationer med två okända är:
8x - 5 = 7y - 9
6x = 3y + 6
Lösningen på detta system skickas in senare i avsnittet Löst övningar.
Linjära ekvationer med absolut värde
Det absoluta värdet på ett verkligt antal är avståndet mellan dess plats på sifferraden och 0 av samma. Att vara ett avstånd är dess värde alltid positivt.
Det absoluta värdet på ett nummer betecknas med modulstänger: │x│. Det absoluta värdet på ett positivt eller negativt antal är alltid positivt, till exempel:
│+8│ = 8
│-3│ = 3
I en ekvation med absolut värde är det okända mellan modulstänger. Tänk på följande enkla ekvation:
│x│ = 10
Det finns två möjligheter, det första är att X är ett positivt antal, i vilket fall vi har:
x = 10
Och den andra möjligheten är att X är ett negativt tal, i detta fall:
x = -10
Dessa är lösningarna på denna ekvation. Låt oss nu se ett annat exempel:
│x+6│ = 11
Beloppet inom staplarna kan vara positivt: då:
x+6 = 11
x = 11 -6 = 5
Eller kan vara negativ. Isåfall:
-(x+6) = 11
-x - 6 = 11 ⇒ -x = 11+6 = 17
Och värdet på det okända är:
x = -17
Denna absoluta värdeekvation har därför två lösningar: x1 = 5 och x2 = -17. Vi kan verifiera att båda lösningarna leder till jämlikhet i den ursprungliga ekvationen:
│5+6│ = 11
│11│ = 11
OCH
│-17+6│ = 11
│-11│ = 11
Enkla lösta övningar
- Övning 1
Lös följande system med linjära ekvationer med två okända:
8x - 5 = 7y -9
6x = 3y + 6
Lösning
Eftersom detta system höjs är det lämpligt för att använda ersättningsmetoden, eftersom den okända i den andra ekvationen x Det är nästan redo för godkännande:
x = (3y + 6)/6
Kan tjäna dig: algebraiskOch du kan omedelbart ersätta den första ekvationen, som sedan blir en första gradsekvation med okänd "y":
8 [(3y + 6)/6] - 5 = 7y - 9
Nämnaren kan undertryckas om varje term multipliceras med 6:
6 . 8⋅ [(3y + 6)/6] - 6.5 = 6 .7y- 6 . 9
8⋅ (3y + 6) - 30 = 42y - 54
Tillämpa distributionsfastigheter under den första terminen till höger om jämlikhet:
24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54
Ekvationen kan förenklas, eftersom alla koefficienter är multiplar på 6:
4y + 3 = 7y - 9
-3y = -12
y = 4
Med detta resultat går vi till clearance av x:
x = (3y +6)/6 → x = (12 +6)/6 = 3
- Övning 2
Lös följande ekvation:
Lösning
I denna ekvation visas produkter, och efter instruktionerna i början måste de utvecklas först:
3x - 10x +14 = 5x + 36x + 12
Då bärs alla termer som innehåller de okända till vänster om jämlikhet, och till höger kommer de oberoende villkoren att vara:
3x - 10x - 5x - 36x = 12 - 14
-48x = -2
x = 1/24
- Övning 3
Genom att lägga till de tre inre vinklarna i en triangel erhålls 180º. Den största överstiger barnet i 35º, och detta överstiger i sin tur i 20 ° skillnaden mellan det största och medium. Vilka är vinklarna?
Lösning
Vi kommer att kalla "X" till huvudvinkeln, "y" till mediet och "z" till barnet. När uttalandet säger att summan av dem är 180º kan du skriva:
x + y + z = 180
Då vet vi att det äldsta överstiger barnet i 35º, vi kan skriva detta:
X = z + 35
Slutligen överstiger barnet 20 º till skillnaden mellan det största och medium:
Z = x - y + 20
Vi har ett system med 3 ekvationer och 3 okända:
x + y + z = 180
X = z + 35
Z = x - y + 20
Genom att rensa den första ekvationen har du:
Z = 180 - x - y
Matchar den tredje:
180 - x - y = x - y + 20
Överför de okända till vänster sida som alltid:
-x - y - x + y = 20 - 180
"Y" avbryts och återstår:
-2x = - 160
x = 80º
Den andra ekvationen är värdet på z:
Z = x - 35 = 80 - 35 = 45º
Och värdet på och är av den första eller tredje:
y = 180 - x - z = 180 - 80 - 45 = 55º
Referenser
- Baldor. 1977. Elementär algebra. Venezuelanska kulturella utgåvor.
- Monterey Institute. Ekvationer, ojämlikheter och absolut värde. Återhämtat sig från: MontereyInstitute.org.
- Online -lärare. Klassificering av linjära eller första gradersekvationer. Återställt från: Professor Inline.Kli.
- Hoffman, J. Urval av matematikfrågor. Volym 2.
- Jiménez, r. 2008. Algebra. Prentice hall.
- Zill, D. 1984. Algebra och trigonometri. McGraw Hill.

