Polynomekvationer

Vad är polynomekvationer?

De Polynomekvationer De är ett uttalande som höjer jämlikheten mellan två uttryck eller medlemmar, där åtminstone ett av termerna som utgör varje sida av jämlikhet är polynomer p (x). Dessa ekvationer namnges enligt graden av deras variabler.

I allmänhet är en ekvation ett uttalande som fastställer jämlikheten mellan två uttryck, där det i åtminstone en av dessa finns okända mängder, som kallas variabler eller okända. Även om det finns många typer av ekvationer, klassificeras dessa vanligtvis i två typer: algebraiska och transcendent.

Polynomiska ekvationer innehåller endast algebraiska uttryck, som kan ha en eller flera okända som ingriper i ekvationen. Enligt den exponent (klass) som de har kan de klassificeras som: första klass (linjär), andra klass (kvadratisk), tredje klass (kubik), fjärde klass (kvantisk), av grad större än eller lika med fem och fem och irrationell.

Egenskaper för polynomekvationer

Polynomiska ekvationer är uttryck som bildas av en jämlikhet mellan två polynomer; Det vill säga för de begränsade summorna av multiplikationer mellan värden som är okända (variabler) och fasta siffror (koefficienter), där variablerna kan ha exponenter, och deras värde kan vara ett positivt heltal, inklusive noll.

Exponenter bestämmer graden eller typen av ekvation. Den termen för uttrycket som har mest värdeeksponent kommer att representera den absoluta graden av polynom.

Polynomiska ekvationer är också kända som algebraiska, deras koefficienter kan vara verkliga eller komplexa siffror och variablerna är okända siffror representerade av en bokstav, till exempel: "X".

Om genom att ersätta ett värde med variabeln "x" i p (x) är resultatet lika med noll (0), sägs det att detta värde uppfyller ekvationen (det är en lösning) och kallas i allmänhet polynometroten.

När en polynomekvation utvecklas vill alla rötter eller lösningar hittas.

Typer av polynomekvationer

Det finns flera typer av polynomekvationer, som är differentierade beroende på antalet variabler, och även enligt deras exponent.

Således är de polynomiska ekvationerna -där dess första termin är ett polynom som bara har en okänd, med tanke på att dess grad kan vara något naturligt antal (n) och den andra termen är noll -kan uttryckas enligt följande:

Kan tjäna dig: historia av trigonometri från dess ursprung

till_{N *} xⁿ + till_{N-1 *} x^N-1 +... + a_{1 *} x¹ + till_{0 *} x₀ = 0

Var:

• till_n, till_N-1 redan₀, De är verkliga koefficienter (siffror).
• till_n skiljer sig från noll.
• Exponent N är ett positivt heltal som representerar ekvationens grad.
• X är den variabel eller okänd som måste sökas.

Den absoluta eller större graden av en polynomekvation är den exponenten med större värde bland alla de som bildar polynom; På detta sätt klassificeras ekvationer som:

Första klass

Den första graden polynomiska ekvationer, även kända som linjära ekvationer, är de som graden (den största exponenten) är lika med 1, polynomet är av formen p (x) = 0; Och det består av en linjär och en oberoende term. Det är skrivet enligt följande:

yxa + b = 0.

Var:

• A och B är verkliga siffror och A ≠ 0.
• Yxa är den linjära termen.
• B är den oberoende termen.

Till exempel ekvation 13x - 18 = 4x.

För att lösa linjära ekvationer måste alla termer som innehåller det okända X överföras till sidan av jämlikhet, och de som inte har rört sig på andra sidan för att rensa det och få en lösning:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

På detta sätt har den givna ekvationen bara en lösning eller rot, vilket är x = 2.

Andra klass

Den andra graden polynomiska ekvationer, även kända som kvadratiska ekvationer, är de där graden (den största exponenten) är lika med 2, polynomet är av formen p (x) = 0 och består av en kvadratisk term, en linjär och en oberoende. Det uttrycks enligt följande:

yxa² + bx + c = 0.

Var:

• A, B och C är verkliga siffror och A ≠ 0.
• yxa² Det är den kvadratiska termen, och "a" är koefficienten för den kvadratiska termen.
• BX är den linjära termen, och "B" är koefficienten för den linjära termen.
• C är den oberoende termen.

Resolut

Generellt ges lösningen på denna typ av ekvationer vid rensning av ekvationens x och förblir på följande sätt, vilket kallas en resolut:

Kan tjäna dig: binomial teorem

Där, (b² - 4ac) kallas diskriminerande från ekvationen och detta uttryck bestämmer antalet lösningar som ekvationen kan ha:

• Ja B² - 4ac) = 0, ekvationen kommer att ha en enda lösning som är dubbel; det vill säga det kommer att ha två lika lösningar.
• Ja B² - 4ac)> 0, ekvationen kommer att ha två olika riktiga lösningar.
• Ja B² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Till exempel har du 4x -ekvationen² + 10x - 6 = 0, för att lösa det först termerna A, B och C identifieras, och sedan ersätts den i formeln:

A = 4

B = 10

C = -6.

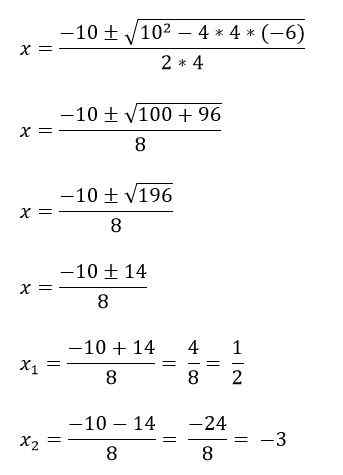
Det finns fall där Second -graders polynomiska ekvationer inte har de tre termerna, och det är därför de löses annorlunda:

• I händelse av att kvadratiska ekvationer inte har den linjära termen (det vill säga B = 0) kommer ekvationen att uttryckas som AX² + C = 0. För att lösa det rensas X² Och fyrkantiga rötter tillämpas i varje medlem och kommer ihåg att de två möjliga tecknen som det okända kan ha:

yxa² + C = 0.

x² = - C ÷ a

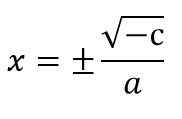
Till exempel 5 x² - 20 = 0.

5 x² = 20

x² = 20 ÷ 5

x = ± √4

x = ± 2

x₁ = 2.

x₂ = -2.

• När den kvadratiska ekvationen inte har en oberoende term (det vill säga C = 0) kommer ekvationen att uttryckas som AX² + Bx = 0. För att lösa det måste den gemensamma faktorn för det okända X tas i den första medlemmen; Eftersom ekvationen matchas med noll uppfylls det att åtminstone en av faktorerna kommer att vara lika med 0:

yxa² + Bx = 0.

x (ax + b) = 0.

På detta sätt måste du:

x = 0.

x = -b ÷ a.

Till exempel: du har ekvation 5x² + 30x = 0. Först är det faktor:

5x² + 30x = 0

x (5x + 30) = 0.

Två faktorer genereras som är x y (5x + 30). En av dessa kommer att betraktas som noll och den andra ges lösning:

x₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

x₂ = -6.

Högsta graden

Huvudgraden polynomiska ekvationer är de som sträcker sig från tredje klass och framåt, som kan uttryckas eller lösas med den allmänna polynomiska ekvationen för någon grad:

Kan tjäna dig: korrelationskoefficient: formler, beräkning, tolkning, exempel

till_{N *} xⁿ + till_{N-1 *} x^N-1 +... + a_{1 *} x¹ + till_{0 *} x₀ = 0

Detta används eftersom en ekvation med en grad större än två är resultatet av faktoriseringen av ett polynom; Det vill säga det uttrycks som multiplikation av grad ett eller högre polynom, men utan riktiga rötter.

Lösningen av denna typ av ekvationer är direkt, eftersom multiplikationen av två faktorer kommer att vara lika med noll om någon av faktorerna är noll (0); Därför måste var och en av de polynomiska ekvationerna lösas och matcha var och en av dess faktorer till noll.

Till exempel har du den tredje gradsekvationen (kubik) x³ + x² +4x + 4 = 0. För att lösa det måste du följa följande steg:

• Villkoren är grupperade:

x³ + x² +4x + 4 = 0

(x³ + x² ) + (4x + 4) = 0.

• Medlemmar bryts ned för att få den gemensamma faktorn för det okända:

x² (x + 1) + 4 (x + 1) = 0

(x² + 4)_*(x + 1) = 0.

• På detta sätt erhålls två faktorer, vilket måste vara lika med noll:

(x² + 4) = 0

(x + 1) = 0.

• Det kan ses att faktorn (x² + 4) = 0 kommer inte att ha en verklig lösning, medan faktorn (x + 1) = 0 ja. Därför är lösningen:

(x + 1) = 0

x = -1.

Löst övningar

Lös följande ekvationer:

Första träning

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Lösning

I detta fall uttrycks ekvationen som multiplikation av polynomer; det vill säga det är faktoriserat. För att lösa det måste varje faktor vara lika med noll:

2x² + 5 = 0, har ingen lösning.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

På detta sätt har den givna ekvationen två lösningar: x = 3 och x = -1.

Andra träning

x⁴ - 36 = 0.

Lösning

Ett polynom gavs, som kan återskrivas som en skillnad i rutor för att nå en snabbare lösning. Således kvarstår ekvationen:

(x² + 6)_*(x² - 6) = 0.

För att hitta lösningen av ekvationerna är båda faktorerna lika med noll:

(x² + 6) = 0, har ingen lösning.

(x² - 6) = 0

x² = 6

x = ± √6.

Således har den initiala ekvationen två lösningar:

x = √6.

x = - √6.