Gibbs Free Energy -enheter, hur det beräknas, lösta övningar

De Gibbs gratis energi (Vanligtvis kallad g) är en termodynamisk potential definierad som skillnaden i entalpi H, utom produkten av temperaturen T, av systemets entropi:

G = h - t s

Gibbs Free Energy mäts i Joules (enligt det internationella systemet), i Ergios (för ligasystemet med enheter), i kalorier eller elektronvolt (För elektromolt).

Figur 1. Diagram som visar definitionen av Gibbs Energy och dess förhållande till de andra termodynamiska potentialerna. Källa: Kärnkraft.netto.

I processerna som förekommer vid konstant tryck och temperatur är variationen av Gibbs fri energi ΔG = ΔH - T ΔS. I sådana processer representerar (g) energin som finns i systemet som kan bli arbete.

Till exempel, i exotermiska kemiska reaktioner, minskar entalpin medan entropin ökar. I Gibbs -funktionen motverkas dessa två faktorer, men först när Gibbs -energin minskar reaktionen sker spontant.

Så om variationen av G är negativ är processen spontan. När Gibbs -funktionen når sitt minimum når systemet en stabil jämvikt. Kort sagt, i en process för vilken tryck och temperatur förblir konstant kan vi bekräfta:

- Om processen är spontan, då ΔG < 0

- När systemet är i balans: ΔG = 0

- I en icke-spontan process ökar den: ΔG> 0.

[TOC]

Hur beräknas det?

Gibbs Free Energy (G) beräknas av definitionen som anges i början:

G = h - t⋅s

I sin tur är entalpi H en termodynamisk potential definierad som:

H = u + p v

- Steg för steg

Därefter kommer en steg -steg -analys att göras för att känna till de oberoende variablerna som Gibbs Energy är en funktion:

1- Av den första termodynamiklagen är intern energi relaterad till systemets entropi och dess volym V för reversibla processer genom differentieringsförhållandet:

Det kan tjäna dig: etidiumbromid: struktur, egenskaper, användningar, toxicitet

DU = DQ - DW = TDS - PDV

Från denna ekvation följer det att intern energi u är en funktion av variablerna S och V:

U = u (s, v)

2- från definitionen av H och att ta skillnaden erhålls:

DH = DU + D (P V) = DU + VDP + PDV

3- Att ersätta uttrycket för du erhållen i (1) Du måste:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Härifrån dras slutsatsen att entalpi H beror på entropi och tryck P, det vill säga:

H = h (s, p)

4- Nu beräknas den totala Gibbs-fria energidifferensen för att få:

DG = DH -TDS ​​-SDT = TDS + VDP -TDS ​​-SDT

Där DH har ersatts av uttrycket som finns i (3).

5- Slutligen, genom att förenkla får du: DG = VDP - SDT, Det är uppenbart att fri energi g beror på trycket och temperaturen t som:

G = g (p, t)

- Maxwells termodynamiska relationer

Från analysen i föregående avsnitt följer det att den inre energin i ett system är en funktion av entropi och volym:

U = u (s, v)

Då skillnaden i ELLER vara:

du = ∂_SU |_V DS + ∂_VU |_S DV = TDS - PDV

Från detta uttryck i partiella derivat kan de så kallade maxwell termodynamiska förhållanden härledas. Partiella derivat gäller när en funktion beror på mer än en variabel och enkelt beräknas genom att tillämpa teoremet i följande avsnitt.

Maxwells första relation

 ∂_VT |_S = -Mon_SP |_V 

För att komma till detta förhållande, Clairaut Theorem - Schwarz på partiella derivat, som säger följande:

"Den andra ordningen blandade derivat med de utbytade variablerna är desamma, förutsatt att de funktioner som ska härledas är kontinuerliga och differentierbara".

Maxwells andra relation

Börjar från vad som visades i punkt 3 i föregående avsnitt:

Kan tjäna dig: Faktorer som påverkar lösligheten

H = H (S, P) och DH = TDS + VDP

Kan erhållas:

 ∂_PT |_S = ∂_SV |_P 

Fortsätt på liknande sätt med Gibbs gratis energi G = g (p, t) och med Helmholtzs fria energi F = f (t, v) För att få de andra två termodynamiska förhållandena i Maxwell. 

figur 2. Josiah Gibbs (1839-1903) var en amerikansk fysiker, kemist och matematiker som gjorde stora bidrag till termodynamik. Källa: Wikimedia Commons.

Maxwells fyra termodynamiska relationer 

1- associerad med intern energi u: ∂_VT |_S = -Mon_SP |_V

2- Den som erhållits från entalpi H: ∂_PT |_S = ∂_SV |_P 

3- Relaterad till energin från Helmholtz F: ∂_TP |_V = ∂_VS |_T 

4- Länkad till den fria energin från Gibbs G: ∂_TV |_P = -Mon_PS |_T

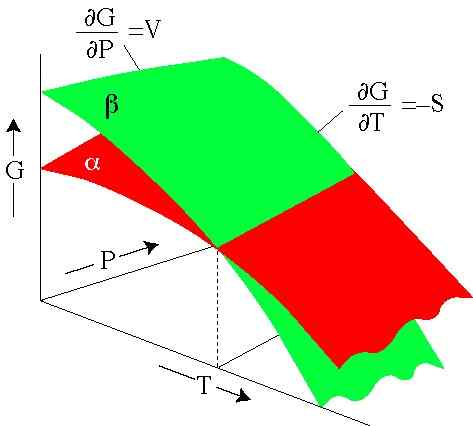figur 2. Gibbs energi beror på tryck och temperatur. Varje yta representerar en fas. (SERC.Carleton.Edu)

Löst övningar

Övning 1

Beräkna variationen av Gibbs Free Energy för 2 mol idealisk gas vid en temperatur på 300K under en isotermisk expansion som leder till det initiala volymsystemet för 20 liter till en slutlig volym av 40 liter.

Lösning

Att komma ihåg definitionen av Gibbs gratis energi är:

G = h - t s

Då kommer en ändlig variation av F att vara:

ΔG = ΔH - T ΔS, Eftersom ΔT = 0

I idealiska gaser beror entalp bara på dess absoluta temperatur, men eftersom det är en isotermisk process, är ΔH = 0 och ΔG = - T ΔS.

För idealiska gaser är entropivariationen i en isotermisk process: 

ΔS = nr ln (v₂/V₁)

Som tillämpades på fallet med denna övning vi har:

ΔS = 2 mol x 8 314 j/(k mol) x ln (40L/20L) = 11,53 j/k

Då kan vi få förändringen i Helmholtzs energi:

ΔG = - 300K x 11,53 J/K = -3457,70 J.

Övning 2

Med hänsyn till att Gibbs fri energi är en funktion av temperatur och tryck g = g (t, p); Bestäm variationen i G under en process där temperaturen inte förändras (isotermisk) för N -mol av en idealisk monoatomisk gas.

Kan tjäna dig: Strontium hydroxid (SR (OH) ₂)

Lösning

Som visas ovan beror förändringen i Gibbs energi endast på förändringen i temperatur T och volym V, så en oändlig variation av den beräknas enligt:

DG = -SDT + VDP

Men om det är en process där temperaturen är konstant, sedan df = + vdp, så en ändlig variation av tryck Δp leder till en förändring i Gibbs -energin som ges av:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Använda den perfekta gasekvationen:

P v = n r t

Under en isotermisk process händer det att:

D (P V) = P DV + V DP = 0

Det är:

dp/p = - dv/v

Så det föregående resultatet kan skrivas beroende på volymvariationen ΔV:

ΔG = + ∫ VDP = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (ΔV)

Övning 3

Med tanke på följande kemiska reaktion:

N₂0 (g) + (3/2) eller₂ (g) ↔no₂ (g) Vid temperatur t = 298 K

Hitta variationen av Gibbs gratis energi och genom det erhållna resultatet, ange om det är en spontan process eller inte.

Lösning

Under stegen:

- Första steget: Reaktionsentalpier

ΔHR = 2*ΔH (nej₂ (g)) - ΔH (n₂0 (g)) = 2*33,2-81,6 = -15,2 kj/mol

- Andra steget: Reaktionsentropivariationen

ΔSr = 2*s (nej₂ (g)) - s (n₂0 (g)) - (3/2) s (eller₂ (g)) = 2*240,1 - 220,1 - 1,5*205,2 = -47,7 j/(mol*k).

- Tredje steg: Variation i Gibbs -funktionen

Detta värde kommer att bestämma balansen mellan minskande energi och ökande entropi för att veta om reaktionen äntligen är spontan eller inte.

ΔGr = ΔHR -T ΔSR = -15.2 -298*(-47.7) = -985.4 J/mol

Eftersom det är en negativ variation av Gibbs Energy kan man dra slutsatsen att det är en spontan reaktion vid temperaturen 298 K = 25 ºC.

Referenser

1. Castaños e. Gratis energiövningar. Återhämtat från: LidiaConlachimica.WordPress.com.
2. Cengel och. 2012. Termodynamik. Sjunde upplagan. McGraw Hill.
3. Librettexts. Gibbs gratis energi. Återhämtad från: kem.Librettexts.org
4. Librettexts. Vad är gratis energi. Återhämtad från: kem.Librettexts.org
5. Wikipedia. Gibbs gratis energi. Återhämtad från: är.Wikipedia.com
6. Wikipedia. Gibbs gratis energi. Hämtad från: i.Wikipedia.com