Translationell balansbestämning, applikationer, exempel

han Translationsbalans Det är ett tillstånd där ett objekt som helhet är när alla krafter som verkar på det kompenseras, vilket resulterar i en tomrumsstyrka. Matematiskt motsvarar det att säga att f₁+ F₂ +  F₃ +.. . = 0, att vara f₁, F₂,  F₃... de involverade krafterna.

Det faktum att en kropp är i translationell balans betyder inte att det nödvändigtvis är i vila. Detta är ett särskilt fall av föregående definition. Objektet kan vara i rörelse, men i avsaknad av acceleration kommer detta att vara en enhetlig rätlinjig rörelse.

Figur 1. Översättningsbalansen är viktig för ett stort antal sporter. Källa: Pixabay.

Så om kroppen är i vila fortsätter. Och om du redan har rörelse kommer det att ha en konstant hastighet. I allmänhet är rörelsen för alla objekt en sammansättning av översättningar och rotationer. Översättningar kan vara som visas i figur 2: linjär eller kröklig.

Men om en av objektets punkter är fixerad är den enda möjligheten att flytta att rotera. Exempel på detta är en CD, vars centrum är fixat. CD -skivan har möjlighet att rotera runt en axel som passerar genom den punkten, men inte att röra sig.

När föremål har fasta punkter eller stöds på ytor är det prat om länkar. Länkarna interagerar begränsar de rörelser som objektet kan göra.

[TOC]

Bestämning av translationell balans

För en partikel i balans är det giltigt att säkerställa att:

F_R = 0

Eller i sammanfattning Notation:

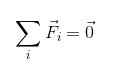
Det är uppenbart att för att en kropp ska vara i translationell balans måste de krafter som agerar på det på något sätt kompenseras, så att resultatet är ogiltigt.

På detta sätt kommer objektet inte att uppleva acceleration och alla dess partiklar är i vila eller experimentera rektilinära översättningar med konstant hastighet.

Det kan tjäna dig: Theory of the Big Bang: Egenskaper, stadier, bevis, problem

Nu, om föremål kan vända, kommer de i allmänhet att göra det. Det är därför de flesta rörelser består av översättnings- och rotationskombinationer.

Ett objekts rotation

När rotationsbalansen är viktig kan det vara nödvändigt att se till att objektet inte vänder. Då måste du studera om det finns moment eller stunder som verkar på den.

Vridmomentet är vektorstorleken på vilken rotationerna beror. Kräver att en styrka tillämpas, men tillämpningspunkten för detta är också viktigt. För att klargöra idén, överväg ett utökat objekt som en kraft verkar F Och låt oss se om du kan producera en rotation med avseende på någon axel eller.

Det är redan intuiterat att genom att trycka på objektet vid punkt P med kraften F, Det är möjligt att vända punkten o, med en anti -horary riktning. Men riktningen i vilken kraft tillämpas är också viktig. Till exempel kraften som tillämpas i figuren av mediet kommer inte att kunna vända föremålet, även om det säkert kan flytta det.

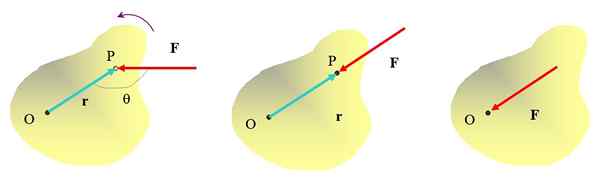figur 2. Olika sätt att tillämpa en kraft på ett omfattande objekt, endast i figuren av extrema lämnade en rotationseffekt erhålls. Källa: Självgjord.

Applicera kraft direkt vid punkten eller kommer inte att användas för att vända objektet heller. Då är det uppenbart att för att uppnå en rotationseffekt måste kraften appliceras på ett visst avstånd från rotationsaxeln och dess verksamhetslinje inte bör gå igenom den axeln.

Definition av vridmoment

Vridmomentet eller ögonblicket för en kraft, betecknad som τ den vektorstorlek som är ansvarig för att sätta ihop alla dessa fakta, definieras som:

τ = r x f

Vektorn r Det är riktat från rotationsaxeln till appliceringspunkten och deltagandet av vinkeln mellan R och F är viktigt. Därför uttrycks storleken på vridmomentet som:

Kan tjäna dig: Newtons första lag: formler, experiment och övningar

τ = r.F.Sen q

Det mest effektiva vridmomentet äger rum när r och F De är vinkelräta.

Om det är önskvärt att det inte finns några rotationer eller dessa pass med konstant vinkelacceleration, är det nödvändigt att summan av momenten som verkar på objektet är ogiltigt, analogt med vad som ansågs för krafterna:

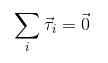
Jämviktsförhållanden

Balans betyder stabilitet, harmoni och balans. För att ett objekts rörelse ska ha dessa egenskaper måste förhållandena som beskrivs i de föregående avsnitten tillämpas:

1) f₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

Det första villkoret garanterar translationsbalansen och den andra rotationen. Båda måste uppfyllas om objektet vill stanna kvar statisk saldo (frånvaro av rörelse av något slag).

Ansökningar

Jämviktsförhållandena är tillämpliga på många strukturer, eftersom när byggnader eller olika föremål byggs, är den gjord med avsikt att deras delar upprätthålls i samma relativa positioner med varandra. Med andra ord, att objektet inte är avväpnad.

Detta är viktigt till exempel när man bygger broar som förblir fast under sina fötter, eller när man utformar bebodda strukturer som inte ändrar position eller har en tendens att dumpa.

Även om det tros att den enhetliga rätlinjiga rörelsen är en extrem förenkling av rörelsen, som vanligtvis förekommer lite i naturen, måste det komma ihåg att ljusets hastighet i tomrummet är konstant och ljudet i luften också, om betraktar homogent för miljön.

I många mobila strukturer tillverkade av människan är det viktigt att en konstant hastighet upprätthålls: till exempel på mekaniska trappor och monteringslinjer.

Det kan tjäna dig: andra lagen om termodynamik: formler, ekvationer, exempel

Exempel på translationell jämvikt

Detta är den klassiska utövandet av spänningar som håller lampan i balans. Det är känt att lampan väger 15 kg. Hitta storleken på de nödvändiga spänningarna för att hålla den i denna position.

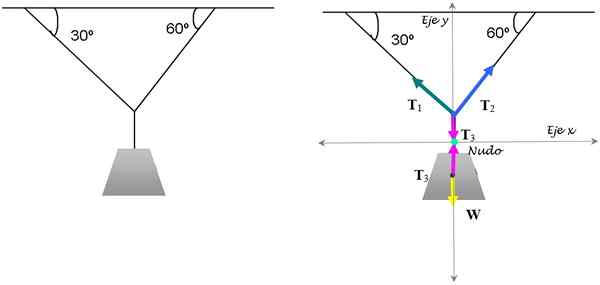Figur 3. Lampbalansen garanteras genom att tillämpa translationsbalansens tillstånd. Källa: Självgjord.

Lösning

För att lösa det fokuserar vi på knuten där de tre strängarna samlas. De respektive gratis kroppsdiagrammen för knuten och för lampan visas i figuren ovan.

Lampans vikt är W = 5 kg . 9.8 m/s² = 49 n. För att lampan ska vara i balans räcker det att det första balansvillkoret uppfylls:

T₃ - W = 0

T₃ = W = 49 n.

Spänningar T₁ och T₂ De måste sönderdelas:

T_1y + T_{2 och} - T₃ = 0 (Summer of Forces längs Y -axeln)))

-T_1x +T_2x = 0 (Summer av krafter längs X -axeln)

Tillämpa trigonometri:

T₁.Cos 60º +t₂ .Cos 30º = 49

- T₁.Sen60º +T₂.Sen30º = 0

Det är ett system med två ekvationer med två okända, vars svar är: T₁ = 24.5 n och T₂ = 42.4 n.

Referenser

1. Rex, a. 2011. Fysikens grunder. Pearson. 76 - 90.
2. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7^ma. Ed. Cengage Learning. 120 - 124.
3. Serway, R., Vule, c. 2011. Fysikens grunder. 9^na Ed. Cengage Learning. 99-112.
4. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. Macgraw Hill. 71 - 87.
5. Walker, J. 2010. Fysik. Addison Wesley. 332 -346.