Normal ansträngning vad den består av, hur det beräknas, exempel

han normal ansträngning Applicerat på ett visst material, även kallad uniaxial ansträngning, är det förhållandet mellan den applicerade kraften vinkelrätt mot en viss yta och tvärsektionsområdet som det verkar, eller belastningen per enhet av området. Matematiskt, om P är storleken på kraften och A är det område där det tillämpas, är ansträngningen σ kvoten: σ = p/a.

Enheterna med normal ansträngning i det internationella systemet är Newton /Metro², känd som Pascal och förkortat PA. Det här är samma tryckenheter. Andra enheter som visas i litteraturen är ofta pund / tum² antingen psi.

Figur 1. Stenar utsätts ständigt för ansträngningar på grund av tektonisk aktivitet, vilket orsakar deformationer i jordskorpan. Källa: Pixabay.

I figur 2 appliceras två krafter med lika stor storlek vinkelrätt på tvärsektionsområdet, vilket gör en dragkraft på den mycket lätta stången som tenderar att förlänga den.

Dessa krafter ger en normal ansträngning som också kallas Axiell belastning centrerad, eftersom dess handlingslinje sammanfaller med den axiella axeln, på vilken centroiden är belägen.

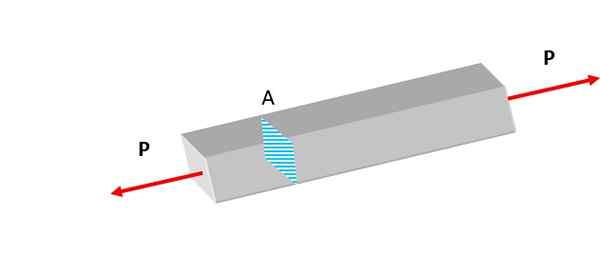figur 2. Den visade stången är föremål för dragkrafter. Källa: Självgjord.

Ansträngningar, vare sig normala eller andra typer, visas kontinuerligt i naturen. I litosfären omfattas klipporna tyngdkraft och tektonisk aktivitet och experimenterar deformationer.

På detta sätt som strukturer som veck och misslyckanden har sitt ursprung, vars studie är viktig för användningen av mineraler och civilingenjör, för byggande av byggnader och vägar, för att nämna några exempel.

[TOC]

Hur beräknas det?

Ekvationen som ges i början σ = P/A gör det möjligt att beräkna den genomsnittliga normala ansträngningen på det aktuella området. Värdet på P är storleken på den resulterande kraften över området som appliceras på centroiden och är tillräckligt för många enkla situationer.

I det här fallet är fördelningen av krafter enhetlig, särskilt vid punkter bort från var du har baren som är föremål för dragkraft eller komprimering. Men om ansträngningen är nödvändig för att beräkna vid en specifik punkt eller krafterna inte fördelas jämnt är det nödvändigt att använda följande definition:

Kan tjäna dig: stängd elektrisk krets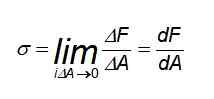

Då kan i allmänhet värdet på ansträngningen vid en viss punkt skilja sig från medelvärdet. I själva verket kan ansträngningen variera beroende på avsnittet att överväga.

Detta illustreras i följande figur, där dragkrafter F försöker separera stången i jämvikt i avsnitten mm och nn.

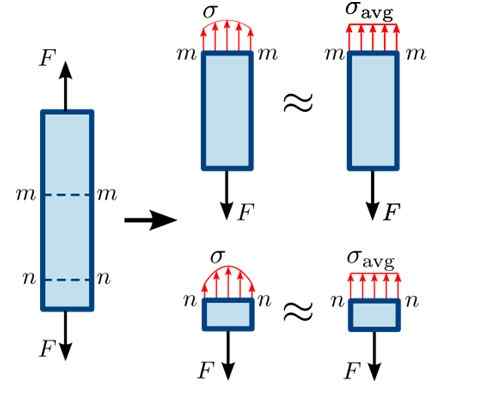Figur 3. Distribution av normala ansträngningar i olika delar av en bar. Källa: https: // commons.Wikimedia.org/wiki/fil: normal_stress.SVG#/Media/File: Normal_Stress.Svg

Som avsnittet nn Det är mycket nära där kraft f ner, fördelningen av krafter på ytan inte är helt homogen, dessa minderåriga är ju längre det är från den punkten. Distributionen är lite mer homogen i avsnittet mm.

I alla fall tenderar den normala ansträngningen alltid att sträcka eller komprimera de två delar av kroppen som finns på båda sidor av det plan som de verkar. Å andra sidan tenderar andra olika ansträngningar, som skjuvning, att röra sig och separera dessa delar.

Hookes lag och normal ansträngning

Hookes lag säger att inom elastiska gränser är den normala ansträngningen direkt proportionell mot den deformation som bar eller objekt upplever. Isåfall:

Normal ansträngning ∝ Enhet deformation

Proportionalitetskonstanten är den unga (y) -modulen:

Normal ansträngning (σ) = ung modul (y) x enhetlig deformation (ε)

σ = y. ε

Med ε = ΔL/L, där ΔL är skillnaden mellan finalen och den initiala längden, som är L.

Den unga modulen eller elasticitetsmodulen är ett kännetecken för materialet, vars dimensioner är desamma som de för ansträngningen, eftersom enhetsdeformationen är dimensionlös.

Det kan tjäna dig: 13 exempel på Newtons andra lag i vardagen

Betydelse av ansträngning i motståndet hos material och geologi

Att bestämma hur resistenta är materialen till ansträngningarna är mycket viktiga. För de strukturer som används vid byggandet av byggnader såväl som i utformningen av delar för olika enheter är det nödvändigt att säkerställa att de material som valts ordentligt uppfyller deras funktion.

Därför analyseras material uttömmande i laboratorier genom försök som är avsedda att veta hur mycket kraft de kan motstå innan deformering och brytning, vilket förlorar sina funktioner. Baserat på detta fattas beslutet om man ska tillverka en viss bit eller vara en del av en enhet.

Det tros att den första forskaren som systematiskt studerade motståndet i materialen var Leonardo da Vinci. Han lämnade bevis på försök där han bestämde motståndet hos ledningar som hänger stenar av olika pesos.

I ansträngningar är både kraftens storlek och även dimensionerna på strukturen och hur den tillämpas är viktigt för att fastställa gränserna inom vilka materialet har ett elastiskt beteende; det vill säga den återgår till sin ursprungliga form när ansträngningen upphör.

Med resultaten från dessa tester utförs ansträngningskurvor för olika typer av material, såsom stål, betong, aluminium och många fler.

Exempel

I följande exempel antas att krafterna fördelas jämnt och att materialet är homogent och isotropiskt. Detta innebär att dess egenskaper är desamma i alla riktningar. Därför är det giltigt att tillämpa ekvationen σ = p/a för att hitta ansträngningar.

-Övning 1

I figur 3 är det känt att den genomsnittliga normala ansträngningen som verkar på AB -sektionen har storleken på 48 kPa på 48 kPa. Hitta: a) storleken på kraften f som verkar i CB, b) ansträngningen på avsnitt BC.

Det kan tjäna dig: Horisontell skjutning: Egenskaper, formler och ekvationer, övningar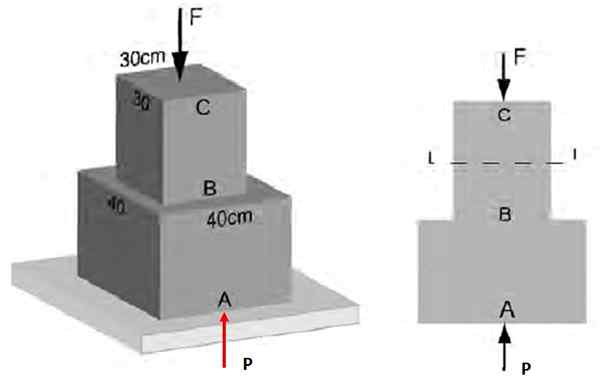Figur 4. Normala ansträngningar på strukturen i exempel 1 ..

Lösning

Eftersom strukturen är i statisk jämvikt, enligt Newtons andra lag:

P-f = 0

Den normala ansträngningen på AB -avsnittet har storlek:

σ_Ab = P/a_Ab

Där p = σ_Ab . TILL_Ab = 48000 PA. (40 x 10 ^-2 m)² = 7680 n

Därför f = 7680 n

Den normala ansträngningen på avsnitt BC är förhållandet mellan storleken på F och tvärsnittets område på den sidan:

σ_{före Kristus} = F/a_{före Kristus} = 7680 N / (30 x 10 ^-2 m)² = 85.3 kpa.

-Övning 2

En 150 m tråd lång och 2.5 mm i diameter sträcker sig av en 500 n kraft. Hitta:

a) Longitudinell ansträngning σ.

b) enhetlig deformation, vet att den slutliga längden är 150.125 m.

c) elasticitetsmodulen OCH av denna tråd.

Lösning

a) σ = f / a = f / π.r²

Trådens radie är hälften av diametern:

R = 1.25 mm = 1.25 x 10^-3 m.

Tvärsektionsområdet är π.r², Då är ansträngningen:

σ = f / π.r² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 pa

b) ε = 5L / l = (slutlig längd - initial längd) / initial längd

Därför:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) Youngs modul av tråden rensas genom att känna till värdena på ε och σ tidigare beräknat:

Y = σ / ε = 101859.2 pa / 0.000833 = 1.22 x 10⁸ PA = 122 MPA.

Referenser

1. Öl, f. 2010. Materialmekanik. Femte. Utgåva. McGraw Hill. 7 - 9.
2. Giancoli, D.  2006. Fysik: Principer med applikationer. 6^tth  Ed. Prentice hall. 238-242.
3. Hibbeler, R.C. 2006. Materialmekanik. Sjätte. Utgåva. Pearson Education. 22 -25
4. Valera Negrete, J. 2005. Allmänna fysikanteckningar. Unk. 87-98.
5. Wikipedia. Stress (mekanik). Återhämtat sig från: Wikipedia.org.