Vanliga faktoregenskaper, exempel, övningar

han vanlig faktor av ett algebraiskt uttryck är ett belopp som finns i alla termer av detta. När den gemensamma faktorn är känd är det möjligt att skriva uttrycket på ett motsvarande sätt genom en produkt av faktorer.

Inte alla algebraiska uttryck har en gemensam faktor, det finns bara de som bara kan delas mellan dem och 1, därför är det inte möjligt att skriva dem som en produkt av faktorer. Ett exempel på uttryck som inte har någon vanlig faktor är:

x + y

Figur 1. Den vanliga faktorn för ett algebraiskt uttryck gör det till den angivna produkten av två faktorer. Källa: Pixabay.

Istället detta ja:

5A + 10B

Man ser att 5 är närvarande i båda termer, eftersom 10 = 5 ∙ 2. Eftersom 5 är den vanliga faktorn, kan följande skrivas:

5A + 10B = 5 ∙ (A + 2B)

Läsaren kan kontrollera genom distribution av egendom, att uttrycket till höger är lika med originalet.

Den vanliga faktorn kan också vara bokstavlig eller en kombination av siffror och bokstäver, till exempel i 4x² - 2x. De x och den 2 De är mellan faktorerna och uttrycket förblir som en produkt:

4x² -2x = 2x⋅ (x -1)

Fördelen med att hitta den gemensamma faktorn för ett uttryck och skriva den som en produkt är att den nästan alltid är lätt att arbeta med den. Det är därför det används i många algebraiska och beräkningsförfaranden som:

-När du löser ekvationer, vars lösningar snabbt avslöjas när den gemensamma faktorn hittas.

-Vid beräkning av en gräns med en obestämdhet kan detta försvinna genom att ordentligt ta fram.

-Lämplig faktorisering underlättar också operationer med rationella algebraiska uttryck, såsom summor och subtraktioner.

[TOC]

Vanliga faktoregenskaper

Huvudegenskaperna för den vanliga faktorn är följande:

-Det kan vara ett nummer, ett algebraiskt uttryck eller en kombination av båda.

-Den vanliga faktorn måste finnas i vart och ett av termerna i uttrycket att faktor.

Kan tjäna dig: transcendenta funktioner: typer, definition, egenskaper, exempel

-Enligt hur mycket villkor som den innehåller kan det vara fallet med:

1. Vanlig monomialfaktor, om den vanliga faktorn är av en enda term,
2. Vanlig binomialfaktor om du har två termer och
3. Vanlig polynomfaktor, om den vanliga faktorn består av flera termer.

Hur man hittar den gemensamma faktorn för ett algebraiskt uttryck?

För att hitta den gemensamma faktorn som finns i ett polynom måste du beräkna den maximala gemensamma divisorn eller MCD för de numeriska koefficienterna för alla termer, såväl som bokstäver eller litterala för varje term och välja kraft med den minsta exponenten.

Bokstäverna eller bokstäverna kan presenteras som monomialer, binomials eller polynomer, som framgår av följande exempel.

Det mest rekommenderade att förstå processen att få den gemensamma faktorn är att följa exemplen och öva på att lösa flera övningar i båda fallen.

Vanliga faktorexempel

Vi får inte förlora det faktum att målet med gemensam faktor omvandlas till en uttryck till en indikerad produkt av faktorer. Sedan analyseras de mest relevanta fallen:

Vanlig monomialfaktor

Du har följande monomialer (Algebraic Expressions):

2x²; 10x⁴och; 100x⁶och²

Vad kan vara den vanliga faktorn för de tre?

Börjar med de numeriska koefficienterna: 2, 10 och 100, alla är jämna och deras MCD är 2. När det gäller den bokstavliga delen är variabel X närvarande i de tre termerna, och den lägsta effekten är x², Då är den vanliga faktorn 2x².

De tre föreslagna termerna kan skrivas som produkter av denna faktor på detta sätt:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²och

100x⁶och²= 2x²∙ 50x⁴och²

Multiplicera faktorerna till höger kan det verifieras att vänsterns termin erhålls.

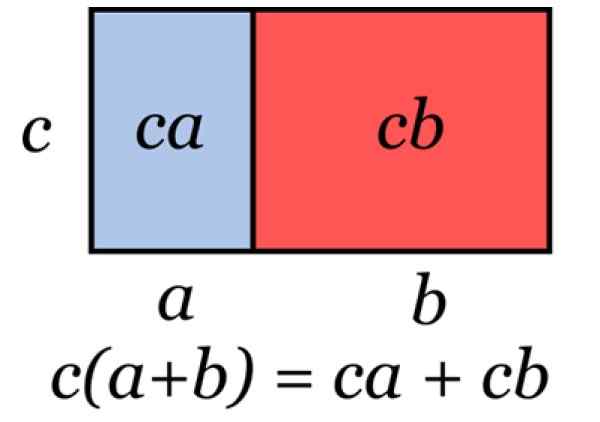figur 2. Illustration som representerar den vanliga faktorn. Källa: Wikimedia Commons.

Denna teknik tillämpas när den behövs för att faktorera ett algebraiskt uttryck, som i följande exempel:

• Exempel 1

Fakta följande uttryck:

Det kan tjäna dig: Isosceles triangel

5x³och + 10x²och² + 5xy²

MCD för de numeriska koefficienterna för varje term är:

MCD (5.10) = 5

När det gäller den bokstavliga delen, båda x som den och De är närvarande i de tre termerna och den minsta exponenten för var och en är 1, därför är den vanliga faktorn 5xy Och du kan skriva:

5x³och + 10x²och² + 5xy²= 5xy ∙ (x² +2xy²+och)

Gemensam polynomfaktor

Den vanliga faktorn kan bestå av en binomial, en trinomial eller i allmänhet i ett polynomialt. I detta fall är instruktionerna i föregående avsnitt fortfarande giltiga och väljer som en vanlig faktor den med den minsta exponenten.

• Exempel 2

Skriv följande uttryck som produkten av två faktorer:

2a (x - 1) - 3b (x - 1)

Genom direkt inspektion är den vanliga faktorn binomialen (X-1), så:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2A - 3B)

Faktorisering genom att gruppera termer

Ibland är förekomsten av en gemensam faktor inte uppenbar, men det avslöjas om termerna grupperas på ett bekvämt sätt:

• Exempel 3

Faktorisera 3x³ - 9ax² - x + 3a

Vid första anblicken finns det ingen vanlig faktor i dessa fyra termer, eftersom till exempel x Det är närvarande i de tre första, men inte i det sista. Och den till Det är i den andra och i det sista ingenting mer.

När det gäller koefficienterna finns det tre termer där de 3 är närvarande, men för att vara en vanlig faktor bör det vara i alla termer.

Det verkar som om de beskrivna teknikerna inte kan tillämpas den här gången. Uttrycket kan emellertid ta hänsyn till genom att gruppera de två första termerna och de två sista, vara försiktiga när man placerar parentesen, att tecknen är lämpliga för att inte ändra originalet:

Kan tjäna dig: rektangulära komponenter i en vektor (med övningar)

3x³ - 9ax² - x + 3a = (3x³ - 9ax²) - (x - 3a)

Notera det negativa tecknet mitt i parentesen: det är nödvändigt, för annars skulle det ursprungliga uttrycket förändras.

I den vänstra parentesen är den vanliga faktorn 3x², därför:

(3x³ - 9ax²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

Och det observeras att en gemensam faktor redan har dykt upp: (x - 3a), Det vill säga, det är faktor för andra gången att få:

3x² (x- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Vanliga faktorövningar

Övning 1

Lös 4x -ekvationen³ +7x²  +6x = 0

Lösning

"X" är därför en vanlig faktor:

3x³ −5x²  +2x = x (3x² −5x +2) = 0

För uttrycket till vänster är det 0, det räcker att ett av dessa två villkor är uppfyllda:

x = 0

ANTINGEN:

3x² −5x +2 = 0

Detta är en komplett andra gradsekvation som kan lösas genom att tillämpa den allmänna formeln, också genom att använda en vetenskaplig kalkylator eller annan algebraisk metod. Lösningarna på denna ekvation är:

x = 1

x = 2/3

När det har hittats är det illustrativt att skriva ekvationen som produkten av tre faktorer, även om uttalandet inte bad om det. Det skulle vara så här:

x⋅ (x-1) ⋅ (x-2/3) = 0

Övning 2

Beräkna följande gräns om den finns:

Lösning

Först ersätts den vid x = −2 för att försöka utvärdera gränsen, därmed erhålls den:

Eftersom det är en obestämdhet i formen 0/0 måste du vara faktor för att försöka eliminera det. Nämnaren kan inte vara faktor, men telleren gör det.

I telleren är den vanliga faktorn x:

x²+2x = x ∙ (x+2)

Det faktoriserade uttrycket ersätts i gränsen och på detta sätt försvinner obestämheten:

Det dras slutsatsen att gränsen finns och är värd −2.

Referenser

1. Baldor, a. 2005. Algebra. Kulturhem.
2. Jiménez, r. 2008. Algebra. Prentice hall.
3. Larson, r. 2012. Förkalkning. 8th. Utgåva. Cengage Learning.
4. Stewart, J. 2007. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
5. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.