Factoring

Vad är faktoriseringen?

Faktorisering är en metod genom vilken ett polynom uttrycks i form av multiplikation av faktorer, som kan vara siffror, bokstäver eller båda. För att faktor är de faktorer som är gemensamma för termerna grupperade, och på detta sätt sönderdelas polynomet i flera polynomer.

Således, när faktorerna multiplicerar med varandra är resultatet det ursprungliga polynomet. Faktorisering är en mycket användbar metod när det finns algebraiska uttryck, eftersom det kan bli multiplikation av flera enkla termer; Till exempel: 2: a² + 2AB = 2A _* (A + B).

Det finns fall där ett polynom inte kan faktoriseras eftersom det inte finns någon vanlig faktor bland dess termer; Således är dessa algebraiska uttryck endast delbara mellan sig och med 1. Till exempel: x + y + z.

I ett algebraiskt uttryck är den vanliga faktorn den maximala gemensamma delaren av termerna som komponerar den.

Faktoriseringsmetoder

Det finns flera faktoriseringsmetoder som tillämpas beroende på fallet. Några av dessa är följande:

Vanlig faktorisering

I denna metod identifieras de faktorer som är vanliga; det vill säga de som upprepas i termerna av uttrycket. Sedan tillämpas den distribuerande egenskapen, den maximala gemensamma divisorn tas bort och faktoriseringen är klar.

Med andra ord identifieras den vanliga faktorn för uttrycket och varje term delas mellan detta; De resulterande termerna kommer att multipliceras med den maximala gemensamma delaren för att uttrycka faktoriseringen.

Exempel 1

Faktorisera (b²x) + (b²och).

Lösning

Först är den vanliga faktorn för varje term, som i detta fall är b², Och sedan är termerna uppdelade mellan den gemensamma faktorn enligt följande:

(b²x) / b² = x

(b²y) / b² = y.

Faktorisering uttrycks, vilket multiplicerar den gemensamma faktorn med de resulterande termerna:

(b²x) + (b²y) = b² (x + y).

Exempel 2

Factorize (2: a²b³) + (3AB²).

Lösning

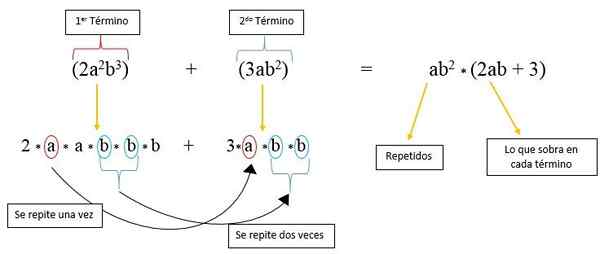
I det här fallet har vi två faktorer som upprepas i varje termin som är "A" och "B", och som höjs till en makt. För att faktorera dem först är de två termerna uppdelade i sin långa form:

2_*till_*till_*b_*b_*B + 3A_*b_*b

Det kan ses att "A" -faktorn upprepas endast en gång under den andra terminen, och "B" -faktorn upprepas två gånger i detta; Så under den första terminen finns det bara 2, en faktor "a" och en "b"; Medan endast i den andra terminen återstår 3.

Därför är det skrivet så många gånger som "A" och "B" upprepas och multipliceras av de faktorer som finns kvar från varje termin, som observerats i bilden:

Grupperingsfaktorisering

Som inte i alla fall uttrycks den maximala gemensamma divisorn av ett polynom tydligt, det är nödvändigt att göra andra steg för att kunna skriva om polynom och därmed faktorisera.

Kan tjäna dig: koniska avsnitt: Typer, applikationer, exempel

Ett av dessa steg är att gruppera termerna för polynom i flera grupper och sedan använda den vanliga faktormetoden.

Exempel 1

Faktorisera AC + BC + AD + BD.

Lösning

Det finns fyra faktorer där två är vanliga: under den första termen är det "C" och i den andra är det "D". På så sätt är de två termerna grupperade och separata:

(AC + BC) + (AD + BD).

Det är nu möjligt att tillämpa den gemensamma faktormetoden, dela varje term efter dess gemensamma faktor och sedan multiplicera den gemensamma faktorn med de resulterande termerna, så här:

(AC + BC) / C = A + B

(ad + bd) / d = a + b

C (A + B) + D (A + B).

Nu erhålls en binomial som är vanligt för båda termerna. För att faktor multipliceras det med de återstående faktorerna; På så sätt måste du:

AC + BC + AD + BD =  (C + D) _* (A + B).

Inspektionsfaktorisering

Denna metod används för att faktor kvadratiska polynomer, även kallade trinomials; det vill säga de som är strukturerade som yxa² ± bx + c, där värdet på "a" skiljer sig från 1. Denna metod används också när trinomialen har X -formen² ± bx + c och värdet på "a" = 1.

Exempel 1

Faktor x² + 5x + 6.

Lösning

Du har ett kvadratiskt trinomial av X -formen² ± bx + c. För att först faktorera det måste två siffror konstateras att, när de multipliceras, resulterar i "C" -värdet (det vill säga 6) och att dess summa är lika med "B" -koefficen. Dessa siffror är 2 och 3:

2 _* 3 = 6

2 + 3 = 5.

På detta sätt förenklas uttrycket enligt följande:

(x² + 2x) + (3x + 6)

Varje term är faktor:

• För (x² + 2x) Den vanliga termen tas bort: x (x + 2)
• För (3x + 6) = 3 (x + 2)

Således kvarstår uttrycket:

x (x +2) +3 (x +2).

Eftersom du har en gemensam binomial för att minska uttrycket multiplicerar det detta med rester av termer och det måste:

x² + 5x + 6 = (x + 2) _* (x + 3).

Exempel 2

Faktorisera 4A² + 12a +9 = 0.

Lösning

Du har ett kvadratiskt trinomial av yxformen² ± bx + c och för att faktorera det multiplicerar allt uttryck genom koefficienten för x²; I det här fallet 4.

4th² + 12a +9 = 0

4th² (4) + 12a (4) + 9 (4) = 0 (4)

16 a² + 12a (4) + 36 = 0

4² till² + 12a (4) + 36 = 0

Nu måste två siffror konstateras att när man multiplicerar med varandra resulterar i värdet av "C" (som är 36) och att när du går med i koefficienten för termen "A", som är 6.

6 _* 6 = 36

6 + 6 = 12.

På så sätt skrivs uttrycket med hänsyn till att 4² till² = 4A _* 4th. Därför tillämpas distribuerande egendom på varje termin:

Kan tjäna dig: Mackinder Box

(4a + 6) _* (4a + 6).

Slutligen är uttrycket uppdelat med koefficienten för en²; det vill säga 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6) / 2) _* ((4a + 6)/ 2).

Uttrycket är som följer:

4th² + 12a +9 = (2a +3) _* (2a + 3).

Faktorisering med anmärkningsvärda produkter

Det finns fall där för att fullständigt faktorera polynomerna med tidigare metoder blir det en mycket lång process.

Det är därför ett uttryck kan utvecklas med formlerna för anmärkningsvärda produkter och därmed blir processen enklare. Bland de mest använda anmärkningsvärda produkterna är:

• Skillnad på två rutor: (a² - b²) = (a - b) _* (A + B)
• Perfekt kvadrat av en summa: a² + 2AB +B² = (a + b)²
• Perfekt kvadrat av en skillnad: a² - 2AB + B² = (a - b)²
• Skillnad på två kuber: a³ - b³ = (a-b)_*(till² + ab + b²)
• Summan av två kuber: a³ - b³ = (a + b) _* (till² - ab + b²)

Exempel 1

Faktorisera (5² - x²)

Lösning

I detta fall finns det en skillnad på två rutor; Därför tillämpas formeln för den anmärkningsvärda produkten:

(till² - b²) = (a - b) _* (A + B)

(5² - x²) = (5 - x) _* (5 + x)

Exempel 2

Faktorisera 16x² + 40x + 25²

Lösning

I det här fallet finns det ett perfekt kvadrat av en summa, eftersom två fyrkantiga termer kan identifieras, och termen kvar är resultatet av att multiplicera två med kvadratroten av den första terminen, vid kvadratroten av den andra terminen.

till² + 2AB +B² = (a + b)²

För att faktor beräknas endast kvadratrötterna för den första och tredje terminen:

√ (16x²) = 4x

√ (25²) = 5.

Sedan uttrycks de två resulterande termerna separerade av tecknet på operationen, och hela fyrkantiga polynomet är förhöjt:

16x² + 40x + 25² = (4x + 5)².

Exempel 3

Faktorisera 27A³ - b³

Lösning

Uttrycket representerar en subtraktion där två faktorer är förhöjda till kuben. För att faktorera dem appliceras formeln för den anmärkningsvärda produkten av skillnaden i kuber, vilket är:

till³ - b³ = (a-b)_*(till² + ab + b²)

För faktor avlägsnas således kubikroten från varje termin av binomialen och multipliceras med kvadratet för den första terminen, plus produkten från den första av den andra terminen, plus den andra termen kvadrat.

27a³ - b³

³√ (27a³) = 3A

³√ (-b³) = -b

27a³ - b³ = (3a - b) _* [(3A)² + 3AB + B²)]]

27a³ - b³ = (3a - b) _* (9A² + 3AB + B²)

Faktorisering med ruffini -regeln

Denna metod används när du har ett polynom av grad större än två för att förenkla uttrycket till flera mindre polynomer.

Exempel 1

Factorice Q (x) = x⁴ - 9x² + 4x + 12

Lösning

Först söks siffrorna som är delare av 12, vilket är den oberoende termen; Dessa är ± 1, ± 2, ± 3, ± 4, ± 6 och ± 12.

Kan tjäna dig: multiplar av 2: vad är och förklaring

Sedan ersätts X av dessa värden, från minst till största, och därför bestäms det med vilka av värdena divisionen kommer att vara exakt; det vill säga resten måste vara 0:

x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

F (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

Och så vidare för varje delare. I detta fall är de faktorer som finns för x = -1 och x = 2.

Ruffini -metoden tillämpas nu, enligt vilken uttryckskoefficienterna kommer att delas upp med de faktorer som hittats så att uppdelningen är exakt. Polynomiska termer beställs från större till lägre exponent; I det fall en term saknas med den grad som följer i sekvensen, placeras en 0 på plats.

Koefficienterna finns i ett schema som ses i följande bild.

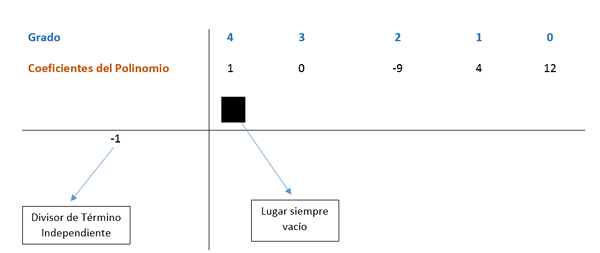
Den första koefficienten sänks och multipliceras av divisorn. I detta fall är den första divisorn -1, och resultatet placeras i följande kolumn. Sedan läggs värdet på koefficienten med det erhållna resultatet vertikalt och resultatet placeras nedan. På så sätt upprepas processen till den sista kolumnen.

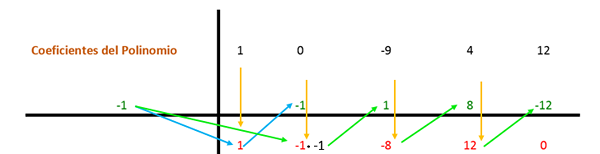
Sedan upprepas samma procedur igen, men med den andra divisorn (som är 2) eftersom uttrycket fortfarande kan förenklas.

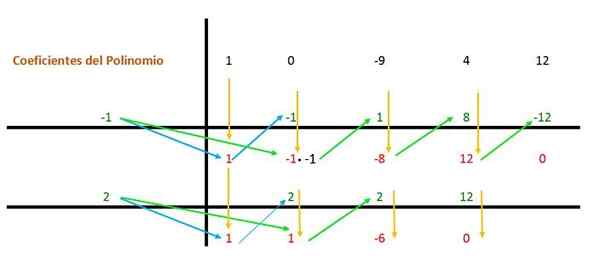
För varje rot som uppnås kommer således att polynomet kommer att ha en term (x - a), där "a" är värdet på roten:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

Å andra sidan bör dessa termer multipliceras med resten som återstod av Ruffini 1: 1 och -6 -regeln, som är faktorer som representerar en examen. På detta sätt är uttrycksformuläret: (x² + X - 6).

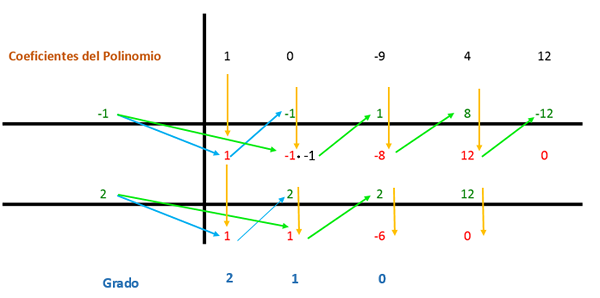
Att få resultatet av polynomfaktorisering med Ruffinis metod är:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (x² + X - 6)

Slutligen kan klass 2-polynom som visas i det föregående uttrycket skrivas om som (x+3) (x-2). Därför är den slutliga faktoriseringen:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Referenser

1. Arthur Goodman, L. H. (nitton nittiosex). Algebra och trigonometri med analytisk geometri. Pearson Education.
2. J, v. (2014). Hur man lär barnen om att fundera på ett polynom.
3. Manuel Morillo, a. S. (s.F.). Grundläggande matematik med tillämpningar.
4. Roelse, s. L. (1997). Linjära metoder för polynomfaktorisering över ändliga fält: teori och implementeringar. Universitets essen.
5. Sharpe, D. (1987). Ringar och faktorisering.