Volymflöde

Vi förklarar vad volumetriskt flöde är, hur man beräknar det och de faktorer som påverkar det

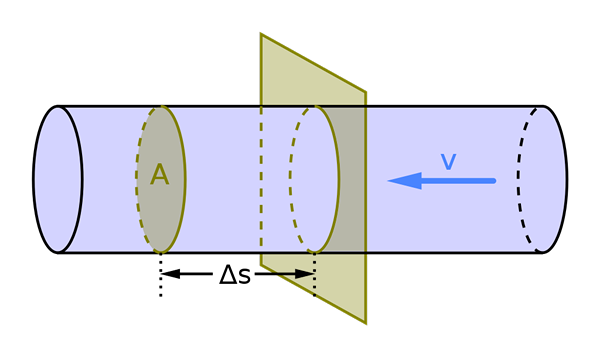
Det volymetriska flödet beror på området för tvärsnitt A och hastigheten på vätska v. Källa: Mikerun, CC BY-SA 4.0, via Wikimedia Commons

Vad är volymetriskt flöde?

han volymflöde Det gör det möjligt att bestämma vätskevolymen som korsar en sektion av kanalen och erbjuder ett hastighetsmått som vätskan rör sig med samma. Därför är dess åtgärd särskilt intressant inom områden som är så olika som industri, medicin, konstruktion och forskning, bland andra.

Att mäta hastigheten på en vätska (antingen en vätska, en gas eller en blandning av båda) är emellertid inte så enkel som förskjutningshastigheten för en fast kropp kan vara att mäta. Därför händer det att det är nödvändigt att veta hastigheten på en vätska.

Från detta och många andra frågor relaterade till vätskor, fysikgrenen känd som vätskemekanikavtal. Flödet definieras som hur flytande en sektion av en kanal går igenom, det är redan en rörledning, en rörledning, en flod, en kanal, en blodomlopp, etc., Med hänsyn till en tillfällig enhet.

Vanligtvis beräknas volymen som ett visst område i en tidsenhet, även kallad volymetriskt flöde. Massan eller massflödet som korsar ett område som bestäms vid en viss tidpunkt definieras också, även om den används mindre ofta än volymetriskt flöde.

Hur beräknas volymetriskt flöde?

Det volymetriska flödet representeras av bokstaven Q. För fall där flödet rör sig vinkelrätt till förarsektionen bestäms det med följande formel:

Q = a = v / t

I denna formel A är det förarens sektion (det är den genomsnittliga hastigheten som vätskan har), V är volymen och T -tiden. Sedan i det internationella systemet mäts området eller avsnittet av föraren i M² Och hastigheten i m/s, flödet mäts m³/s.

Kan tjäna dig: 21 viktiga händelser i fysik

För fall där hastigheten på vätskekomling skapar en vinkel θ med riktningen vinkelrätt mot ytavsnittet A, är uttrycket för att bestämma flödet som följer:

Q = a cos θ

Detta överensstämmer med den tidigare ekvationen, eftersom när flödet är vinkelrätt mot område A, θ = 0 och därför cos θ = 1.

Ovanstående ekvationer är bara sanna om vätskehastigheten är enhetlig och om avsnittet är platt är platt. Annars beräknas det volymetriska flödet genom följande integral:

Q = ∫∫_s v d s

I denna integrerade DS är det ytvektorn, bestämd av följande uttryck:

Ds = n ds

Där är N den normala enhetsvektorn till ytan på kanalen och DS ett differentiellt ytelement.

Kontinuitetsekvation

Ett kännetecken för inkomprimerbara vätskor är att vätskans massa bevaras med två sektioner. Det är därför kontinuitetsekvationen uppfylls, vilket skapar följande förhållande:

ρ₁ TILL₁ V₁ = ρ₂ TILL₂ V₂

I denna ekvation ρ är vätskans densitet.

För fall av regimer i permanent flöde, där densiteten är konstant och därför uppfylls det att ρ₁ = ρ₂, Det reduceras till följande uttryck:

TILL₁ V₁ = A₂ V₂

Detta motsvarar att bekräfta att flödet bevaras och därför:

Q₁ = Q₂.

Från observationen av ovanstående följer det att vätskorna accelererar när de når en smalare sektion av en kanal, medan de minskar sin hastighet när de når en bredare del av en kanal. Detta faktum har intressanta praktiska tillämpningar, eftersom det gör det möjligt att leka med hastigheten för förskjutning av en vätska.

Kan tjäna dig: subatomära partiklar

Bernoulli -princip

Bernoulli -principen bestämmer att för en idealisk vätska (det vill säga en vätska som varken har viskositet eller friktion) som rör sig i en cirkulationsregime genom en stängd kanal uppfylls att dess energi förblir konstant under hela dess förskjutning.

I slutändan är Bernoulli -principen inget annat än formuleringen av energibesparingslagen för flödet av en vätska. Således kan Bernoulli -ekvationen formuleras enligt följande:

H +v² / 2g+p/ ρg = konstant

I denna ekvation är h höjden och g är tyngdkraften.

I Bernoulli -ekvationen beaktas energin hos en vätska när som helst, energi som består av tre komponenter.

• En kinetisk komponent som inkluderar energi på grund av hastigheten med vilken vätskan rör sig.
• En komponent som genereras av gravitationspotentialen, som en följd av höjden vid vilken vätskan är belägen.
• En del av flödesenergi, som är den energi som en vätska har på grund av trycket.

I detta fall uttrycks Bernoulli -ekvationen enligt följande:

H ρ g +(v² ρ)/2 + p = konstant

Logiskt sett, i fallet med en verklig vätska är uttrycket av Bernoulli -ekvationen inte uppfylld, eftersom det i förskjutningen av vätskan finns friktionsförluster och det är nödvändigt att ta en mer komplex ekvation.

Vad som påverkar volymetriskt flöde?

Det volymetriska flödet kommer att påverkas om det finns en hinder i kanalen.

Kan tjäna dig: Lätt brytning: Element, lagar och experiment

Dessutom kan det volymetriska flödet också förändras genom effekt av temperatur- och tryckvariationstemperaturen och det tryck som det är.

Enkel metod för att mäta volymetriskt flöde

En riktigt enkel metod för att mäta det volymetriska flödet är att låta en vätskeflöde inom en mätbehållare under en viss tidsperiod.

Denna metod är i allmänhet inte särskilt praktisk, men sanningen är att den är extremt enkel och mycket illustrativ att förstå betydelsen och vikten av att känna till flödet av en vätska.

På detta sätt får vätskan strömma in i en mätbehållare under en tidsperiod, den ackumulerade volymen mäts och resultatet som erhålls mellan den förflutna tiden är uppdelad.

Referenser

1. Flöde (vätska) (n.d.).  I Wikipedia. Återhämtad från ES.Wikipedia.org.
2. Volymetrisk flödeshastighet (n.d.).  I Wikipedia. Hämtas från.Wikipedia.org.
3. Ingenjörer Edge, LLC. "Fluid Volumetric Flow Rate Equation". Kantingenjörer
4. Mott, Robert (1996). "1". Applicerad vätskemekanik (4: e upplagan). Mexiko: Pearson Education.
5. Batchelor, g.K. (1967). En introduktion till vätskedynamik. Cambridge University Press.
6. Landau, L.D.; LIFSHITZ, E.M. (1987). Flytande mekanik. Teoretisk fysiks kurs (2: a upplagan.). Pergamonpress.