Fraktioner motsvarande 3/4

De Fraktioner motsvarande 3/4 De är de där, genom att dela telleren mellan nämnaren, resulterar det i decimalnumret 0.75.

Det är alltid möjligt. Om resultatet av denna operation är lika med 0.75, fraktionen motsvarar 3/4, till exempel fraktion 6/8:

Fraktion 6/8 motsvarar ¾, eftersom genom att dela teller mellan nämnaren i båda fallen 0 erhålls 0.75. Källa: f. Zapata.

Nu erhölls fraktion 6/8 genom att multiplicera både telleren och ¾ nämnaren. Genom att samtidigt multiplicera telleren och nämnaren med samma mängd ändras inte decimalvärdet för en given fraktion, men gör det möjligt att få fraktioner som motsvarar en given.

Ett annat sätt att hitta en bråkdel som motsvarar en annan skulle vara att dela teller och nämnare med samma mängd. Men när det gäller ¾ är det inte möjligt att hitta ett sådant nummer som delar sig samtidigt till 3 och 4 och resultatet är heltal. Detta beror på att 3 och 4 är kusiner med varandra, så de har inte vanliga delare.

När telleren och nämnaren för en bråkdel är primtal med varandra, sägs det att fraktionen är oreducerbar. Därför är ¾ oåterkallelig.

Sätt att hitta en bråkdel som motsvarar en annan

Det finns två mycket enkla sätt att hitta en bråkdel som motsvarar en annan given bråk: den första är genom reduktion och den andra genom förstärkning.

Minskning och förstärkning av fraktioner

Minskning

Denna procedur består av att hitta ett nummer som är delare av både telleren och nämnaren. När både teller och nämnaren har hittats delas både teller och nämnaren med detta värde och erhålls omedelbart en bråkdel som motsvarar originalet. Det verifieras att det således gör tellerförhållandet mellan nämnaren och jämförelse.

Kan tjäna dig: matematiska funktioner

När den oåterkalleliga fraktionen av en annan. Den således erhållna fraktionen är oåterkallelig.

Fraktionen ¾ är oåterkallelig, som nämnts tidigare, för att vara 3 och 4 kusiner med varandra, men följande metod tillåter oändliga fraktioner motsvarande ¾.

Förstärkning

För att förstärka en given fraktion måste telleren och nämnaren multipliceras med samma mängd, oavsett om det är ett positivt eller negativt antal. Till exempel erhölls fraktion 6/8 genom att förstärka ¾ efter faktor 2:

Även om fraktioner har en annan teller och nämnaren är båda desamma.

Notera följande figur, som innehåller två identiska cirklar, uppdelade i lika delar, även om det är av olika storlek. Omsorgsfullt observerar har områdena i grönt och lila samma mått, men det gröna området har delats upp i 3 delar, av de 4 totalt som utgör vänstercirkeln. Å andra sidan delades cirkeln till höger i 8 lika delar och det lila området motsvarar 6 av dem.

På detta sätt kan du grafera att ¾ motsvarar 6/8, eftersom båda fraktionerna representerar samma mängd.

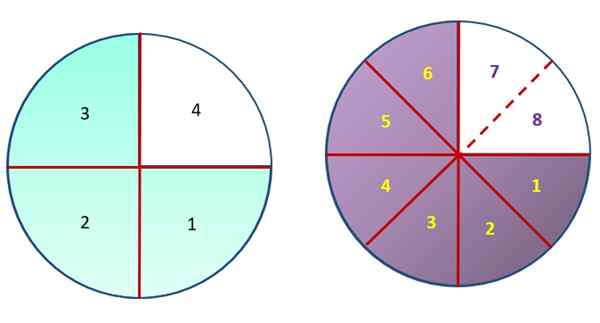Fraktioner ¾ och 6/8 representerar samma område i båda kretsarna. Källa: f. Zapata.

I allmänhet, om fraktionen multipliceras ¾ med nummer N, erhålls så många fraktioner motsvarande den som du vill:

Det är viktigt att notera att N aldrig kan vara lika med 0, eftersom divisionen med 0 inte är definierad. Ingen fraktion kan ha 0 i din nämnare.

Hur man vet om en bråkdel motsvarar 3/4?

Som förklarats i början är ett sätt att veta om en bråkdel motsvarar ¾ att göra kvoten mellan telleren och nämnaren. Om det är 0.75, fraktionen motsvarar ¾, men det finns ett par metoder att veta, som inte kräver division direkt:

Det kan tjäna dig: Vägt media: Hur det beräknas, exempel och övningar

Metod 1

Anta att fraktion A/B, och du vill veta om det motsvarar ¾, det vill säga om det är sant att:

För att vara likvärdig måste produkt 4 vara lika med produkt 3B:

4a = 3b

Metod 2

Om fraktion A/B motsvarar ¾, och delar A och B med den maximala gemensamma MCD -divisorn, måste resultatet vara ¾.

För att klargöra användningen av dessa metoder, se följande exempel.

Exempel

Exempel 1

Bestäm om fraktion 150/200 motsvarar ¾:

Efter metod 1

I detta fall A = 150 och B = 200 måste det uppfyllas att:

4a = 3b

• 4 × 150 = 600
• 3 × 200 = 600

Det dras slutsatsen att 150 /200 motsvarar ¾.

Efter metod 2

Den maximala gemensamma delaren på 150 och 300 delar dem båda exakt. Båda mängderna sönderdelas i sina främsta faktorer och sedan multipliceras vanliga faktorer med deras minsta exponent:

• 150 = 2 × 5² × 3
• 200 = 2³ × 5²

De 2 och 5 är vanliga, de multiplicerar väljer den minsta kraften som de dyker upp med:

MCD (150, 200) = 2 × 5² = 2 × 25 = 50

Nu fortsätter vi att dela:

Löst övningar

Övning 1

Skriv med förstärkning Fem fraktioner motsvarande ¾, multiplicera teller och nämnaren varje gång med följande hela siffror:

a) 3, b) 5, c) (-2), d) 10 och e) 20

Lösning till

Lösning B

Lösning C

Observera att det inte finns någon skillnad genom att förstärka fraktionen med 2 eller -2, eftersom enligt teckenregeln är kvoten som anges mellan två negativa mängder positiv.

Lösning D

Lösning E

Observera att denna fraktion är densamma som erhålls genom förstärkning med 2 den fraktion som erhållits ovan:

Övning 2

Kontrollera om följande fraktioner motsvarar ¾:

Det kan tjäna dig: Rektangulära koordinater: Exempel och övningar löst

a) 18/24; b) 21/28; c) 24/32; d) 27/38; e) 33/44

Lösning till

Använda metod 1 som beskrivs ovan:

4a = 3b

För fraktion 18/24 måste du = 18 och b = 24, sedan:

• 4 × 18 = 72
• 3 × 24 = 72

Därför är 18/24 och 3/4 likvärdiga.

Lösning B

Enligt metod 2 måste vi hitta den maximala gemensamma divisorn (MCD) på 21 och 28, dela sedan både med resultatet, och om 3/4 -fraktionen erhålls är de likvärdiga:

21 = 3 × 7
28 = 4 × 7 = 2²× 7

Den vanliga faktorn är 7, därför MCD (21,28) = 7, sedan:

Lösning C

För denna övning kontrolleras det om kvoten mellan 24 och 32 är 0 0.75:

24 ÷ 32 = 0.75

Sedan är 24/32 motsvarande 3/4.

Lösning D

I fraktion 27/38 observeras att 38 inte är en multipel av 4, därför motsvarar den inte 3/4. Hur som helst, förhållandet mellan 27 och 38 utförs:

27 ÷ 38 = 0.710526

Varav det dras slutsatsen att 27/38 inte motsvarar 3/4.

Lösning E

Det är lätt att se att fraktion 33/44 erhålls genom att multiplicera telleren och nämnaren på 3/4 med 11, så här:

Därför är de likvärdiga.