Konvergent linsegenskaper, typer och träning löst

De Konvergerande linser De är de som är tjockare i sin centrala och tunnare del vid kanterna. Som en konsekvens koncentrerar de sig (konvergerar) i en enda punkt de ljusstrålar som påverkar dem parallellt med huvudaxeln. Denna punkt kallas fokus eller bildfokus och representeras med bokstaven f. Konvergerande eller positiva linser bildar vad som kallas riktiga bilder av objekt.

Ett typiskt konvergent linsexempel är ett förstoringsglas. Det är emellertid vanligt att hitta denna typ av linser på mycket mer komplexa enheter som mikroskop eller teleskop. I själva verket är ett basiskt sammansatt mikroskop som utgörs av två konvergerande linser som har ett litet fokalavstånd. Dessa linser kallas mål och okulär.

Förstoringsglas, en konvergent lins. 

Konvergerande linser används i optik för olika applikationer, även om det kanske är mest känt är att korrigera synfel. Således indikeras de att hantera.

[TOC]

Egenskaper

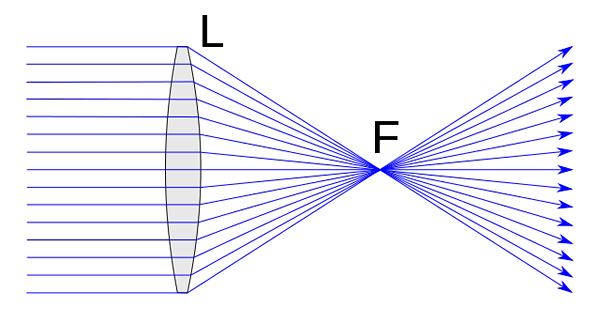Konvergent objektiv. Chetvorno [CC0]

Konvergerande linser har en seriefunktioner som definierar dem. I alla fall är det kanske det viktigaste vad vi redan har avancerat i dess definition. Således kännetecknas konvergerande linser av att avleda genom fokus varje stråle som påverkar dem i en riktning parallellt med huvudaxeln.

Dessutom, på ett ömsesidigt sätt, bryts varje incidentstråle som passerar fokus parallellt med linsens optiska axel.

Konvergerande linser element

Mot bakgrund av din studie är det viktigt att veta vilka element som utgör linserna i allmänhet och konvergerande linser i synnerhet.

I allmänhet kallas det det optiska centrumet för en lins till den punkt som varje stråle som passerar genom den inte upplever någon avvikelse.

Huvudaxeln är linjen som ansluter sig till det optiska centrumet och huvudfokuset, som vi redan har kommenterat som representeras med bokstaven F.

Kan tjäna dig: ton: transformationer, ekvivalenser och övningar löst

Det kallas huvudfokus till den punkt där alla strålar som påverkar linsen parallellt med huvudaxeln finns.

Avståndet mellan det optiska centrumet och fokus kallas fokalavstånd.

Krökningscentra definieras som centrumen för sfärerna som skapar linsen; Att å andra sidan är radionerna av krökning radionerna på sfärerna som ger upphov till linsen.

Och slutligen kallas det optiskt plan till linsens centrala plan.

Bilderbildning i konvergerande linser

Mot bakgrund av bildningen av bilder i konvergerande linser måste en serie grundläggande regler som förklaras nedan beaktas.

Om strålen påverkar linsen parallellt med axeln, konvergerar den framväxande strålen i fokusbilden. Omvänt, om en incidentstråle korsar objektfokuset, dyker upp blixt i en riktning parallellt med axeln. Slutligen bryts de strålar som korsar det optiska centret utan att uppleva någon avvikelse.

Som en konsekvens kan du i en konvergent lins ge följande situationer:

- Att objektet är beläget med avseende på det optiska planet på ett avstånd större än dubbelt så mycket som fokalavståndet. I så fall är bilden som inträffar verklig, inverterad och mindre än objektet.

- Att objektet är beläget på avstånd från det optiska planet lika med två gånger fokalavståndet. När detta händer är den erhållna bilden en riktig, inverterad bild och samma storlek som objektet.

- Att objektet är på avstånd från det optiska planet mellan en gång och två gånger fokalavståndet. Så en bild produceras är verklig, inverterad och större än det ursprungliga objektet.

- Att objektet är beläget på avstånd från det optiska planet lägre än fokalavståndet. I så fall kommer bilden att vara virtuell, direkt och större än objektet.

Kan tjäna dig: magnetisk chock: enheter, formler, beräkning, exempel

Typer av konvergent lins

Det finns tre olika typer av konvergerande linser: biconvex -linser, planokonvexlinser och concavoconvex -linser.

Biconvex -linser, som namnet antyder, består av två konvexa ytor. Planoconvexas har under tiden en plan yta och en annan konvex. Och slutligen utgörs concavoconvex -linser av en något konkav yta och en annan konvex.

Skillnad med divergerande linser

Konvergent objektiv. FIR0002 (samtal) (uppladdningar) [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Divergerande linser skiljer sig å andra sidan från det konvergent genom att tjockleken minskar från kanterna mot mitten. I motsats till vad som hände med konvergent, i denna typ av linser är ljusstrålarna som påverkar huvudaxeln parallellt. På detta sätt bildar de vad som kallas virtuella bilder av objekt.

I optik används divergerande eller negativa linser, som de också är kända, främst för att korrigera myopi.

Gauss -ekvationer av tunna linser och ökad lins

I allmänhet är den typ av linser som studeras de som kallas tunna linser. Dessa definieras som de som har en liten tjocklek jämfört med krökningen av ytorna som begränsar dem.

Denna typ av lins kan studeras med Gauss -ekvationen och med ekvationen som gör det möjligt att bestämma ökningen i en lins.

Gauss -ekvation

Gauss -ekvationen av tunna linser tjänar till att lösa många grundläggande optikproblem. Därför dess stora betydelse. Ditt uttryck är som följer:

1/f = 1/p +1/q

Där 1/ f är det som kallas kraften hos en lins och f är fokalavståndet eller avståndet från det optiska centret till focam. Måttenheten för en linsens kraft är dioptern (d), som är 1 d = 1 m^-1. För sin del är P och Q respektive avståndet vid vilket ett objekt och det avstånd till vilket dess bild observeras.

Det kan tjäna dig: Theory of the Big Bang: Egenskaper, stadier, bevis, problem

Ökad lins

Den laterala ökningen i en tunn lins erhålls med följande uttryck:

M = - q / p

Där M är ökningen. Från värdet på ökningen kan en serie konsekvenser dras:

Ja | M | > 1, bildstorleken är större än objektets

Ja | M | < 1, el tamaño de la imagen es menor que el del objeto

Om m> 0 är bilden rätt och på samma sida av linsen som objektet (virtuell bild)

Ja m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)

Träning löst

En kropp är belägen en meter från en konvergent lins, som har ett fokalavstånd på 0, 5 meter. Hur kommer bilden av kroppen att vara? Hur långt hittar du?

Vi har följande data: p = 1 m; F = 0,5 m.

Vi ersätter dessa värden i Gauss -ekvationen för de tunna linserna:

1/f = 1/p +1/q

Och följande återstår:

1/0,5 = 1 + 1/Q; 2 = 1 + 1/q

Vi rensar 1/q

1/q = 1

För att sedan rensa Q och få:

Q = 1

Därifrån ersätter vi i ekvationen av ökningen i en lins:

M = -q / p = -1 / 1 = -1

Därför är bilden verklig sedan q> 0, inverterad eftersom m < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.

Referenser

1. Ljus (n.d.). I Wikipedia. Hämtad den 18 mars 2019 från detta.Wikipedia.org.
2. Lekner, John (1987). Reflektionsteori, av elektromagnetiska och delvågor. Kandare.
3. Ljus (n.d.). I Wikipedia. Hämtad den 20 mars 2019 från.Wikipedia.org.
4. Lins (n.d.). I Wikipedia. Hämtad den 17 mars 2019 från detta.Wikipedia.org.
5. Lins (optik). I Wikipedia. Hämtad den 19 mars 2019 från.Wikipedia.org.
6. Acts, Eugene (2002). Optik (4: e upplagan.). Addison Wesley.
7. Tupler, Paul Allen (1994). Fysisk. 3: e upplagan. Barcelona: Jag vände.