Coulomb Law förklaring, formel och enheter, övningar, experiment

De Coulomb Law Det är den fysiska lagen som reglerar samspelet mellan elektriskt laddade föremål. Det anges av den franska forskaren Charles Augustin de Coulomb (1736-1806), tack vare resultaten från hans experiment genom torsionsbalans.

1785 upplevde Coulomb otaliga tider med små elektriskt laddade sfärer, till exempel att föra eller bort två sfärer, varierande storleken på dess last och dess tecken. Alltid titta på och noggrant registrera varje svar.

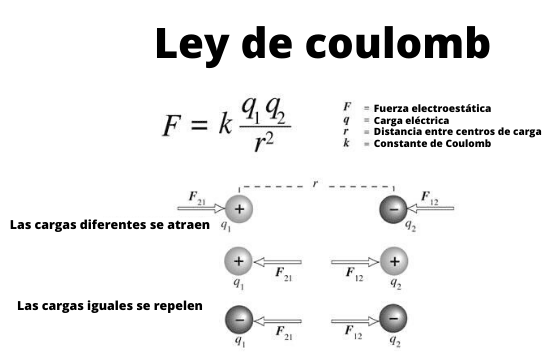
Figur 1. Schema som visar samspelet mellan specifika elektriska avgifter genom Coulombs lag.

Dessa små sfärer kan betraktas som specifika belastningar, det vill säga objekt vars dimensioner är obetydliga. Och de uppfyller, som är kända sedan tiden för de forntida grekerna, att belastningarna på samma tecken avvisas och de med olika tecken lockas.

figur 2. Militäringenjör Charles Coulomb (1736-1806) anses vara den viktigaste fysikern i Frankrike. Källa: Wikipedia Commons.

Med detta i åtanke hittade Charles Coulomb följande:

-Kraften av attraktion eller avstötning mellan två specifika laddningar är direkt proportionell mot produkten av storleken på belastningarna.

-Denna kraft är alltid riktad längs linjen som ansluter sig till belastningarna.

-Slutligen är kraftens storlek omvänt proportionell mot kvadratet på avståndet som skiljer belastningarna.

[TOC]

Formel och enheter i Coulomb -lagen

Tack vare dessa observationer drog Coulomb slutsatsen att kraftens storlek F Mellan två specifika avgifter q₁ och q₂, separerade ett avstånd r, Det ges matematiskt som:

Eftersom kraft är en vektorstorlek, för att uttrycka den, är en enhetsvektor helt definierad r I riktning mot linjen som förenar lasterna (en enhetsvektor har storlek lika med 1).

Dessutom kallas den nödvändiga proportionalitetskonstanten omvandling av det tidigare uttrycket till en jämlikhet_och eller helt enkelt K: The elektrostatisk antingen Coulomb.

Slutligen upprättas Coulomb -lagen för punktliga belastningar, ges av:

Kraften, som alltid i det internationella enhetssystemet, kommer i Newton (N). När det gäller avgifterna kallas enheten Coulomb (c) för att hedra Charles Coulomb och slutligen kommer avståndet R i meter (m).

Att uppmärksamma den tidigare ekvationen är det uppenbart att den elektrostatiska konstanten måste ha enheter av N.m² / C², För att få Newtons som ett resultat. Konstantens värde bestämdes experimentellt som:

Kan tjäna dig: gratis vektorer: egenskaper, exempel, övningar

k_och = 8.89 x 10 ⁹ N.m² / C² ≈ 9 x 10 ⁹ N.m² / C²

Figur 1 illustrerar interaktionen mellan två elektriska laddningar: När de är samma tecken avvisas de, annars lockar de.

Observera att Coulombs lag passar Newtons tredje lag eller reaktionslag, därför storleken på F₁ och F₂ De är desamma, adressen är densamma, men sinnena är motsatta.

Hur man tillämpar Coulombs lag

För att lösa interaktioner mellan elektriska laddningar måste följande beaktas:

- Ekvationen tillämpas uteslutande i fallet med specifika belastningar, det vill säga elektriskt laddade föremål men av mycket små dimensioner. Om laddade objekt har mätbara dimensioner är det nödvändigt att dela upp dem i mycket små belastningar och sedan lägga till bidrag från var och en av dessa laster, för vilka omfattande beräkning krävs.

- Elektrisk kraft är en vektorstorlek. Om det finns mer än två laddningar som interagerar, nettokraften på lasten q_Yo Det ges av superpositionsprincipen:

F_Netto = F_i1 + F_I2 + F_i3 + F_i4 +... = ∑ F_{I j}

Där abonnemanget J Vale 1, 2, 3, 4 ... och representerar var och en av de återstående lasterna.

- Det måste alltid vara förenligt med enheterna. Det vanligaste är att arbeta med den elektrostatiska konstanten i enheter om du måste se till att lasterna är i Coulomb och avståndet i meter.

- Slutligen tillämpas ekvationen när belastningarna är i statisk balans.

Löst övningar

- Övning 1

I följande figur finns det två specifika laster +Q och +2q. En tredje punktlig belastning -q placeras på P. Det uppmanas att hitta den elektriska kraften på denna belastning på grund av närvaron av de andra.

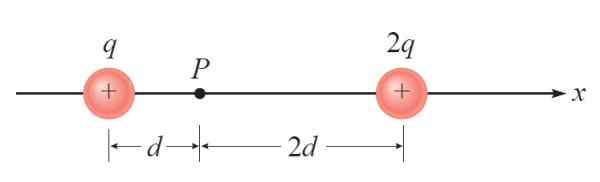Figur 3. Diagram för året löst 1. Källa: Giambattista, a. Fysik.

Lösning

Det första är att upprätta ett lämpligt referenssystem, som i detta fall är den horisontella axeln eller x -axen. Ursprunget till detta system kan vara var som helst, men genom komfort kommer det att placeras i P, som visas i figur 4A:

Kan tjäna dig: Bethelgeuse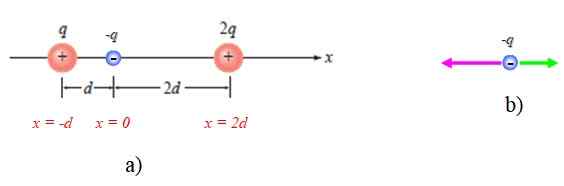Figur 4. Årets schema löst 1. Källa: Giambattista, a. Fysik.

Ett schema av krafterna på -q visas också med hänsyn till att det lockas till de andra två (figur 4B).

Låt oss ringa F₁ Till kraften som utövar belastningen som på belastningen -q riktas de längs x -axeln och pekar i negativ mening, därför:

Enhetsvektorn i riktning mot x -axeln är x Med en circumflex -accent i ekvationen. Detta är en vanlig notation för en enhetsvektor. Desto mindre teckna visas eftersom kraften F₁ pekar i den negativa betydelsen av axeln.

Analog beräknas F₂:

Observera att storleken på F₂ Det är hälften av F₁, Även om lasten är dubbel. För att hitta nettokraften läggs de äntligen till vektor F₁ och F₂:

F_Netto = (-k + k/2).(Fråga² /d²) (x) N = - (k/2).(Fråga² /d²) (x) N

- Övning 2

Två polystyren sfäriter med lika mass m = 9.0 x 10^-8 kg har samma positiva belastning q och är suspenderade av en sidentråd i längd l = 0,98 m. Sfärerna är separerade ett avstånd på d = 2 cm. Beräkna värdet på.

Lösning

Situationen för uttalandet beskrivs i figur 5A.

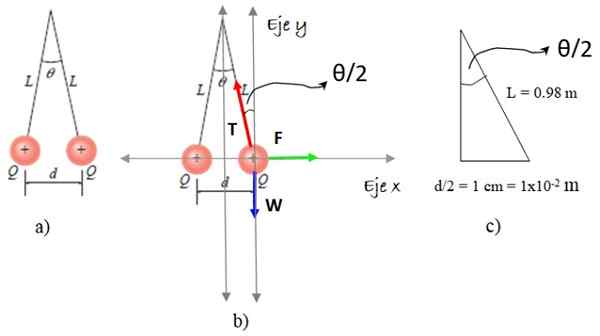Figur 5. Scheman för upplösning av övning 2. Källa: Giambattista, a. Fysik /f. Zapata.

Vi valde en av sfäriterna och på den ritar vi det isolerade kroppsdiagrammet, som innehåller tre krafter: vikt W, Repspänning T och elektrostatisk avstötning F, Som visas i figur 5b. Och nu stegen:

Steg 1

Värdet på θ/2 beräknas med triangeln i figur 5C:

θ/2 = Arcsen (1 x 10^-2/0.98) = 0.585º

Steg 2

Då måste du tillämpa Newtons andra lag och match 0, eftersom avgifterna är i statisk balans. Det är viktigt att lyfta fram den spänningen T Den är benägen och har två komponenter:

∑f_x = -T.synd θ + f = 0

∑f_och = T.cos θ - w = 0

Steg 3

Vi rensar storleken på spänningen i den sista ekvationen:

Det kan tjäna dig: dynamik: historia, vilka studier, lagar och teorier

T = w/ cos θ = mg/ cos θ

Steg 4

Detta värde ersätts i den första ekvationen för att hitta storleken på F:

F = t sin θ = mg (sin θ / cos θ) = mg. Tg θ

Steg 5

Som f = k q² /d², Det rensar Q:

Genom att ersätta de numeriska värdena som tillhandahålls av uttalandet erhålls det:

Q = 2 × 10^-elva C.

Experiment

Att kontrollera Coulombs lag är enkel med hjälp av en torsionsbalans som liknar den som används i hans laboratorium.

Det finns två små sfärer av Saúco, varav en, den i mitten av balansen, är avstängd från en tråd. Experimentet består av att röra vid Saúco -sfärerna nedladdade med en annan metallfär laddad med belastning Q.

Figur 6. Coulombs torsionsbalans.

Omedelbart fördelas lasten lika mellan de två Saúco -sfärerna, men då, liksom massor av samma tecken, avvisar de. En kraft som orsakar trådens torsion från tråden och flyttar omedelbart bort från den fasta sfären på den hängande sfären.

Då ser vi att det sträcker sig några gånger tills balansen når. Sedan vridningen av stången eller tråden som håller den balanseras av den elektrostatiska avstötningskraften.

Om sfärerna ursprungligen var vid 0, kommer nu den mobila sfären att ha vänt en vinkel θ. Omger balansen finns det en kandidatband i grader för att mäta denna vinkel. När de tidigare bestämmer vridkonstanten beräknas lätt avstötningskraften och värdet på den last som förvärvats av Saúco -sfärerna.

Referenser

1. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Volym 5. Elektrostatik. Redigerad av Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysik. Andra upplagan. McGraw Hill.
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Resnick, r. 1999. Fysisk. Vul. 2. 3: e upplagan. på spanska. Kontinentala redaktionella företag s.TILL. av C.V.
5. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 2.