Hess förklaringslag, applikationer, exempel

De Hessrätt Det är en annan manifestation av energibesparingslagen som gör det genom enkla algebraiska summor att bestämma entalpin av en kemisk reaktion genom en kemisk reaktion. Förstås av entalpi när värmen släpps eller absorberas, vid konstant tryck, som är förknippat med någon kemisk reaktion eller kemiskt fenomen.

Entalpies, ΔH, bestäms experimentellt med kalorimetri. Det finns emellertid reaktioner som är svåra att studera med denna teknik. När detta händer används andra reaktioner som deras specifika entalpier har och som har de intressen eller föreningar som intresserar.

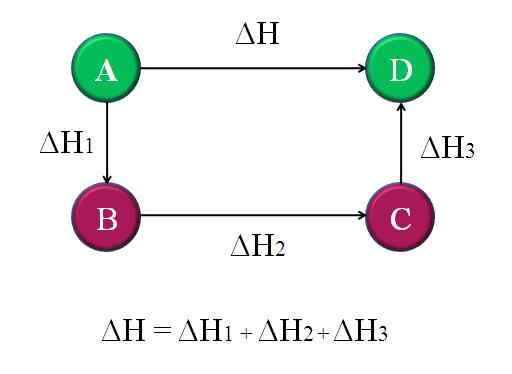
Enkelt och allmänt diagram där Hess -lagen för fyra kemiska reaktioner tillämpas. Källa: Gabriel Bolívar.

På detta sätt kan reaktionens "okända" ΔH beräknas. Till exempel hjälper toppdiagrammet att förstå denna idé. Det finns fyra reaktioner: A-D, A-B, B-C och C-D. A-D-reaktionen är den som har den största ΔH, för i vilken de inträffar, så att säga, de mest ökända kemiska förändringarna.

De andra reaktionerna har, medan de har mindre ΔH, eftersom de består av alternativa steg eller alternativa reaktioner för att nå samma produkter D. Därför summan av ΔH₁, ΔH₂ och ΔH₃, Det kommer att vara lika med Δh. Att veta detta, ΔH eller någon annan entalpi, kan beräknas genom att tillämpa enkla rensningar. Det här är Hesss lag.

Hesss lag är mycket användbar vid beräkning av reaktionsentalpier, samt träningsentalpier för olika föreningar eller instabila mellanhänder.

[TOC]

Förklaring av Hesss lag

Beräkning av entalpin av en reaktion

Anledningen till att det uppfylls det:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Det beror på att entalpin, eller förändringen av entalpi, är en tillståndsfunktion. Detta innebär att deras värden inte modifieras av antalet steg, steg eller mellanhandsreaktioner. Till exempel kommer Δh att förbli densamma även när det finns en Δh₁₀ som bör övervägas i den algebraiska summan.

Entalpier kan visualiseras som topparna på vissa berg. Oavsett hur stegen mot dem riktas kommer höjden som skiljer dem från marnivån aldrig att variera. Och exakt är det de höjder som läggs till eller subtraheras för att bestämma den okända höjden på ett omgivande berg.

Återvänder till det föregående diagrammet: A, det är ett berg, ett annat berg, och så vidare. Höjdskillnaden mellan A- och D -toppar är den största. Att lägga till höjderna mellan A-B, B-C och C-D kommer det att ge lika med A-D-höjd. Detta är vad som görs med entalpierna i deras respektive kemiska reaktioner.

Kan tjäna dig: fosfatgrupp

Entalpi av en reaktion från entalpier av formationer

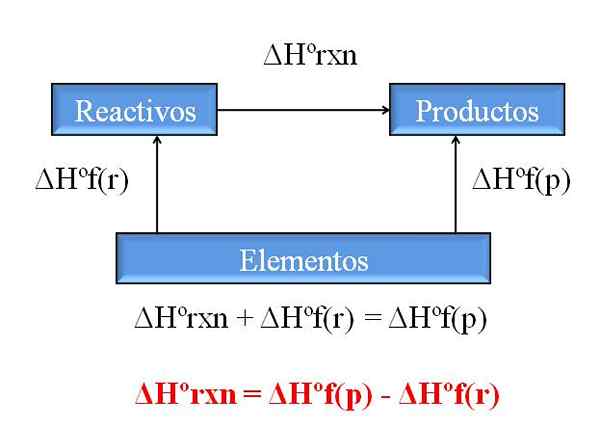Allmänt diagram för att beräkna entalpin av en reaktion från entalpier av formationer. Källa: Gabriel Bolívar.

En av de mest värdefulla konsekvenserna av Hess lag är att den tillåter bestämning av entalpierna för någon kemisk reaktion, med utbildningsentalpier från alla föreningar (reagens och produkter).

Den överlägsna bilden illustrerar denna punkt. Förstås av entalpi av tillhörande värmeformation när en förening bildas från dess element. Denna entalpi skulle bli den maximala möjliga skillnaden mellan reagens och produkter, utan att behöva konsultera andra kemiska reaktioner; Åtminstone utanför den separata träningen av föreningar.

Hur läser du diagrammet den här gången? Ett trick är alltid att lägga till entalpierna när det går i pilens riktning och subtrahera dem när pilen är på motsatt väg. Således lägger ΔHºrxn, standardreaktionsentalpi, till ΔHºF (reagens), standard entalpi av reagensbildning, och de subtraheras ΔHºF (produkter), standard entalpi för produktbildning av produkter.

Reaktioner summor

Diagrammen kan bli mycket komplicerade att tolka, särskilt när det finns många reaktioner som måste beaktas. Därför används summan av reaktionerna. Denna metod underlättar i hög grad beräkningen av entalpier och påskyndar förståelsen av Hesss lag.

Anta till exempel att du vill bestämma ΔHºrxn för följande reaktion:

A + B + C → ABC

Och vi har också två andra reaktioner:

A + B → AB (ΔHº₁)

AB + C → ABC (ΔHº₂)

Det är intressant att A + B + C är på vänster sida (reagens) och att ABC är på höger sida (produkter). Sedan fortsätter vi helt enkelt att lägga till de två senaste reaktionerna:

A + B → AB

AB + C → ABC

A + AB + C → ABC + AB

Som AB är från båda sidor elimineras det. Och så har vi:

A + B + C → ABC

ΔHºrxn = ΔHº₁ + ΔHº₂

Att lägga till reaktionerna utelämnas användningen av något diagram.

Tillämpningar av Hesss lag

Hesss lag tillåter, utan behov av experiment, entalpier för olika kemiska reaktioner eller fenomen. Några av dem listas ner:

- Träningsentalpier för instabila föreningar eller mellanhänder, som vi vanligtvis har i organisk kemi.

-Entalpier av fasövergångar, i studien av kristallina fasta ämnen.

Kan tjäna dig: kemisk förening

-Entalpier av allotropa övergångar, till exempel den mellan grafit och diamant.

På samma sätt används Hess lag för att bestämma en fast energi för ett fast ämne och de elektroniska affiniteterna hos vissa atomer.

Exempel: Löst övningar

- Exempel 1

Beräkna ΔHRXN för följande reaktion:

2HCl (g) + F₂(g) → 2HF (L) + Cl₂(g)

Om du har följande reaktioner och deras respektive entalpier:

4HCl (g) + eller₂(g) → 2h₂Eller (l) + 2cl₂(g) (ΔH = -202.4 kJ/mol)

1/2h₂(g) + 1/2f₂(g) → HF (L) (ΔH = -600.0 kJ/mol)

H₂(g) + 1/2o₂(g) → h₂Eller (l) (Δh = -285.8 kJ/mol)

Ekvationer beställning

Till att starta måste vi lägga till reaktionerna på ett sådant sätt att HCl och F₂ är på vänster sida och HF och CL₂, På höger sida. Men viktigare, det märker att så mycket h₂ Som h₂Eller är inte i intresseekvationen. Därför måste vi avbryta dem i summan och göra de stökiometriska koefficienterna sammanfaller genom multiplikationer:

2HCl (g) + 1/2₂(g) → h₂Eller (l) + cl₂(g) (ΔH = -202.4 kJ/mol) * (1/2)

Denna ekvation multiplicerades med 1/2 för att ha 2HCL istället för 4HCL

H₂(g) + f₂(g) → 2HF (L) (ΔH = -600.0 kJ/mol) * (2)

Denna ekvation multiplicerades med 2 för att ha f₂ och nr 1/2f₂

H₂Eller (l) → h₂(g) + 1/2o₂(g) (Δh = -285.8 kJ/mol) * (-1)

Under tiden multiplicerades den senare med -1 för att "vända det". Således har vi de ordnade ekvationerna och redo att lägga till.

Summan av ekvationerna

Att lägga till allt ger oss:

2HCl (g) + 1/2₂(g) → h₂Eller (l) + cl₂(g) (ΔH = -101.2 kJ/mol)

H₂(g) + f₂(g) → 2HF (L) ΔH = -1200.0 kJ/mol)

H₂Eller (l) → h₂(g) + 1/2o₂(g) (ΔH = 285.8 kJ/mol)

2HCl (g) + F₂(g) → 2HF (L) +Cl₂(g)

Observera att termer 1/2₂, H₂Eller och h₂ De avbryts för att de är på båda sidor av pilen. Entalpies läggs också till, vilket ger:

ΔHrx = 285.8 kJ/mol + (-101.2 kJ/mol) + (-1200.0 kJ/mol)

Detta uttryck är detsamma som början:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Och så har vi att ΔHRX är lika med:

ΔHRX = -1015.4 kJ/mol

- Exempel 2

I det här exemplet kommer det att ses att de entusiastiska reaktionerna motsvarar de entrealier av intresseföreningar.

Det är önskvärt att bestämma ΔHRXN för nästa nedbrytningsreaktion:

2so₃(g) → 2so₂(g) + eller₂(g)

Och utbildningsentalpierna för SO -föreningarna räknas till hands₃ Och så₂:

S (s) + o₂(g) → så₂(g) (ΔH = -296.8 kJ/mol)

Kan tjäna dig: Isopreno: Struktur, egenskaper, applikationer

S (s) + 3/2o₂(g) → så₃(g) (ΔH = -395.6 kJ/mol)

Ekvationer beställning

Denna övning kommer att lösas på samma sätt som föregående exempel. Det borde vara så₃ ha rätt och multiplicera med 2. För det måste vi "vända" SO -formationsekvationen₃ multiplicera det med -1 och sedan genom att multiplicera det med 2:

2so₃(g) → 2s (s) + 3o₂(g) (ΔH = -395.6 kJ/mol) * (-2)

SO -formationsekvationen₂ Vi multiplicerar det också med 2:

2s (s) + 2: a₂(g) → 2so₂(g) (ΔH = -296.8 kJ/mol) * (2)

Summan av ekvationerna

Nu läggs ekvationerna till:

2so₃(g) → 2s (s) + 3o₂(g) (ΔH = 791.2 kJ/mol)

2s (s) + 2: a₂(g) → 2so₂(g) (ΔH = -593.6 kJ/mol)

2so₃(g) → 2so₂(g) + eller₂(g)

Observera att termen 2s elimineras eftersom det är på båda sidor av pilen. Också 3: e₂ 2o är subtraherad₂ ger en o₂. Summan av entalpierna, och därför kommer värdet på ΔHRXN att vara:

ΔH = ΔHrxn = 791.2 kJ/mol + (-593.6 kJ/mol)

= 197.6 kJ/mol

Som alla nedbrytningsreaktioner är den endoterm, så dess entalpi är positiv.

Alternativ metod

Det finns en metod för att nå samma resultat på ett mer direkt och enkelt sätt. Detta nämndes i ett tidigare avsnitt.

2so₃(g) → 2so₂(g) + eller₂(g)

För att bestämma ΔHRXN för denna reaktion måste vi beräkna ΔHºF (reagens) och ΔHºF (produkter). ΔHºF (så₃) är lika med -395.6 kJ/mol, medan ΔHºF (så₂) är lika med -296.8 kJ/mol. ΔHºF (eller₂) är lika med 0, eftersom elementärt syre finns som en molekyl av O₂ och inte som atomer eller fria.

Så vi har:

ΔHrxn = ΔHºF (produkter) - ΔHºF (reagens)

= [ΔHºF (så₂) + ΔHºF (eller₂)] - ΔHºF (så₃)

= ΔHºF (så₂) - ΔHºF (så₃)

Vi måste emellertid multiplicera båda träningsentalpierna med 2 för att matcha de stökiometriska koefficienterna med avseende på den kemiska ekvationen:

ΔHrxn = 2ΔHºF (så₂) - 2ΔHºF (så₃)

Och beräkna vi har:

ΔHrxn = 2 (-296.8 kJ/mol) - 2 (-395.6 kJ/mol)

= 197.6 kJ/mol

I själva verket är det så som det vanligtvis föredras att lösa alla övningar där Hess -lagen tillämpas.

Referenser

1. Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning.
2. Wikipedia. (2020). Hesss lag. Hämtad från: i.Wikipedia.org
3. Cohen Shelly. (18 maj 2020). Hesss lag. Kemi librettexts. Återhämtad från: kem.Librettexts.org
4. Clark Jim. (2010). Hess's Law and Entalppy Change Caldo. Återhämtat sig från: Chemguide.co.Storbritannien
5. Helmestine, Anne Marie, PH.D. (11 februari 2020). Hess's Law Definition. Återhämtat sig från: tankco.com
6. Foist Laura. (2020). Hess's Law: Definition, Formula & Exempel. Studie. Återhämtat sig från: studie.com
7. Quimitube. (2014). Teori 14 Termokemi: Beräkning av entalpin av en reaktion genom Hess's Law. Återhämtat sig från: Quimitube.com