Fermat begränsar vad som består och övningar löst

han Fermatgräns Det är en numerisk metod som används för att uppnå värdet på lutningen på en linje, som är tangent till en specifik funktion av dess domän. Det används också för att få kritiska punkter för en funktion. Hans uttryck definieras som:

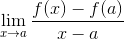
Det är uppenbart att Fermat inte visste grunden för härledningen, men det var hans studier som främjade en grupp matematiker att fråga om tangentlinjer och deras tillämpningar i beräkningen.

[TOC]

Vad är Fermats gräns?

Den består av ett tillvägagångssätt på 2 poäng, som under tidigare förhållanden utgör en Secant -linje till funktionen med korsningen i par av värden.

När du närmar sig variabeln till "A" -värdet är poängparet skyldiga att träffas. På detta sätt blir den tidigare torkningslinjen tangent till punkten (a; f (a)).

Kitientvärdet (x - a), när det utvärderas i punkt "a", kastar en obestämdhet av typ k -gränser mellan noll (k/0). Där dessa obestämningar kan brytas genom olika faktoriseringstekniker.

De mest använda operationsteknikerna är:

-Fyrkantig skillnad (a² - b² ) = (a + b) (a - b); Elementets förekomst (A-B) innebär i stora delar av fallen den faktor som förenklar uttrycket (X-A) i Fermat-gränsförhållandet.

- Fyrkantig slutförande (AX² + bx); Efter avslutad rutor erhålls en Newton -binomial, där en av dess två faktorer förenklas med uttrycket (x - a), vilket bryter obestämheten.

- Konjugat (a + b) / (a ​​+ b); Multiplicera och dela uttrycket genom konjugatet av någon faktor kan vara till stor hjälp för att bryta obestämheten.

- Vanlig faktor; I många fall är resultatet av att använda telleren för Fermat f (x) - f (a) dold för faktorn (x - a) nödvändig för att faktorisera. För detta observeras det noggrant vilka element som upprepas i varje faktor i uttrycket.

Fermat Limit Application för maximalt och minimum

Även när Fermats gräns inte skiljer sig mellan maximalt och minimum.

Baskunskap om den grafiska teorin om funktioner vid konuntning med detta teorem, kan vara tillräcklig för att fastställa maximala och minimivärden mellan funktioner. Faktum är att böjningspunkter kan definieras av teoremet för det extra medelvärdet till Fermats teorem.

Den kubik- liknelsen

Den viktigaste paradoxen för Fermat kom när man studerade den kubikliknande liknelsen. Eftersom hans uppmärksamhet riktades mot tangentlinjerna för en funktion för en given punkt, stötte han på problemet med att definiera nämnda tangentlinje vid den befintliga böjningspunkten i funktionen.

Det verkade omöjligt att bestämma tangentlinjen till en punkt. Således börjar den undersökning som skulle ge upphov till den differentiella beräkningen. Sedan definieras av viktiga exponenter för matematik.

Maximus och minimous

Studien av maximalt och minimum av en funktion var en utmaning för klassisk matematik, där en entydig och praktisk metod för definitionen av dessa.

Fermat skapade en metod baserad på drift av små differentiella värden, som efter faktoriseringsprocesser elimineras genom att ge plats för det mest och minimala värdet.

Denna variabel måste utvärderas i det ursprungliga uttrycket för att bestämma koordinaten för nämnda punkt, som tillsammans med analytiska kriterier kommer att definieras av det maximala eller minimum av uttrycket.

Metod

I sin metod använder Fermat Vietas bokstavliga symbolik, som bestod av exklusiv användning av stora bokstäver: vokalerna, för de okända och konsonanterna för de kända mängderna.

När det gäller radikala värden implementerade Fermat en viss process, som senare skulle användas i faktoriseringarna av obestämda gränser oändlighet mellan oändligheten.

Denna process består av att dela varje uttryck med det differentiella värdet som används. När det gäller Fermat använde bokstaven E, där uppdelningen mellan den största kraften i E, det värde som söks från den kritiska punkten blir tydligt.

Historia

Fermats gräns är i själva verket ett av de minst kända bidragen i den långa listan över matematikern. Hans studier var från primtal för att i princip skapa baserna för beräkning.

I sin tur var Fermat känd för sina excentricitet angående hans hypoteser. Det var vanligt för en slags utmaning för tidens andra matematiker, när han redan hade lösningen eller demonstrationen.

Det hade ett stort utbud av tvister och allianser med olika matematiker från tiden, som älskade eller hatar att arbeta med honom.

Hans sista teorem var det huvudsakliga ansvaret för hans världsberömmelse, där han sa att en generalisering av Pytagoras teorem För alla "n" -grader var det omöjligt. Sägs ha en giltig demonstration av det, men dog innan han offentliggjorde den.

Denna demonstration var tvungen att vänta ungefär 350 år. 1995 avslutade matematikerna Andrew Wiles och Richard Taylor, ångesten som lämnades av Fermat och visade att han hade rätt genom en giltig demonstration av sitt sista teorem.

Övningar

Övning 1

Definiera lutningen på linjen tangent till kurvan f (x) = x² Vid punkten (4, 16)

Ersätta i uttrycket av fermatgränsen du har:

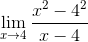
Sedan tillämpa fyrkantiga minimum Tellerna är faktor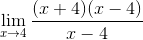

Faktorerna förenklas (x - 4)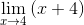

När du utvärderar har du

M = 4 + 4 = 8

Övning 2

Definiera den kritiska uttryckspunkten f (x) = x² + 4x med hjälp av Fermat -gränsen

I det här fallet finns det ingen koordinat, så X -värdet ersätts av den generiska formen x₀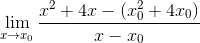

En strategisk gruppering av element utförs och försöker gruppera X-X-kamrater₀

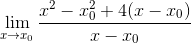
Squares utvecklas

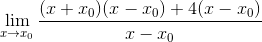
Den vanliga faktorn X-X observeras_{0 och extraheras}

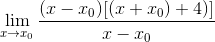
Uttrycket kan redan förenklas och obestämdhet bryts

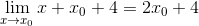
I minsta punkter är det känt att lutningen på tangentlinjen är lika med noll. På detta sätt kan vi matcha noll uttrycket och rensa X -värdet₀    

2 x₀ + 4 = 0

X₀ = -4/2 = -2

För att få den saknade koordinaten behöver du bara utvärdera punkten i den ursprungliga funktionen

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

Den kritiska punkten är P (-2, -4).

Referenser

1. Verklig analys. En historisk strategi Sauhl Stahl, John Wiley & Sons, 5 augusti. 1999.
2. Den matematiska karriären för Pierre av Fermat, 1601-1665: andra upplagan. Michael Sean Mahoney. Princeton University Press, 5 juni. 2018
3. Från Fermat till Minkowski: Föreläsningar om teorin om siffror och dess historiska utveckling. W. Scharlau, h. Opolka, Springer Science & Business Media, 1985
4. Fermats sista teorem: En genetisk introduktion till algebraisk nummerteori. Harold m. Edwards. Springer Science & Business Media, 14 jan. 2000
5. Fermat Days 85: Matematik för optimering. J.-B. Hiriart-Uruty Elsevier, 1 jan. 1986