Rätlinjär rörelseegenskaper, typer och exempel

han rätlinje rörelse Det är en där mobilen rör sig längs en rak linje och därför passerar i en dimension, och därmed får också namnet Ojämnrörelse. Denna raka linje är bana eller sökväg följt av objektet som rör sig. Bilarna som reser längs Avenue i figur 1 följer denna typ av rörelse.

Detta är den enklaste rörelsemodellen som kan föreställas. De dagliga rörelserna hos människor, djur och saker kombinerar ofta överföringar i en rak linje med rörelser längs kurvor, men vissa observerar ofta vissa som uteslutande är rektilinala.

Figur 1. Bilar som rör sig längs en rätlinjig väg. Källa: Pixabay.

Här är några bra exempel:

- När du kör längs ett 200 -meter rätlinjigt spår.

- Kör bil på en rak väg.

- Släpper ett objekt fritt från en viss höjd.

- När en boll kastas vertikalt.

https: // giphy.com/gifs/j5xx3bynaqv06wtoxq

Nu uppnås målet att beskriva en rörelse genom att specificera egenskaper som:

- Placera

- Förflyttning

- Fart

- Acceleration

- Tid.

För att en observatör ska upptäcka rörelsen av ett objekt är det nödvändigt att ha en referenspunkt (ursprung O) och har upprättat en specifik adress att flytta, vilket kan vara axeln x, axeln och eller någon annan.

När det gäller objektet som rör sig kan detta ha otaliga sätt. Det finns inga begränsningar i detta avseende, men i allt som följer kommer det att antas att mobilen är en partikel; ett så litet objekt att dess dimensioner inte är relevanta.

Det är känt att detta inte är fallet för makroskopiska objekt; Det är emellertid en modell med goda resultat i beskrivningen av en objekts globala rörelse. På detta sätt kan en partikel vara en bil, en planet, en person eller något annat föremål som rör sig.

Vi kommer att börja vår studie av rätlinjiga kinematik med en allmän inställning till rörelsen och sedan kommer vissa fall att studeras som de som redan utsetts.

[TOC]

Allmänna egenskaper hos den rätlinjiga rörelsen

Följande beskrivning är allmän och tillämplig på alla typer av en dimensionell rörelse. Det första är att välja ett referenssystem. Linjen längs vilken rörelsen äger rum kommer att vara axeln x. Parametrarna för rörelsen:

Placera

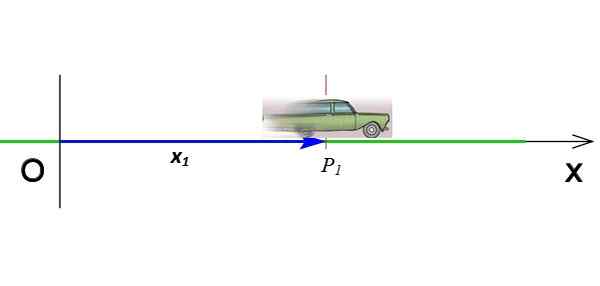figur 2. Position för en mobil som rör sig på X -axeln. Källa: Wikimedia Commons (modifierad av F. Zapata).

Det är vektorn som går från ursprunget till den punkt där objektet är på ett ögonblick givet. I figur 2, vektorn x₁ Anger mobilen när den är i koordinaten P₁ och med tiden t₁. Positionsvektorenheterna i det internationella systemet är mätare.

Förflyttning

Förskjutning är vektorn som indikerar förändringen i position. I figur 3 har bilen gått från positionen P₁ till ståndpunkt P₂, Därför är dess förskjutning 5x = x₂ - x₁. Förskjutning är subtraktionen av två vektorer, den symboliseras med den grekiska bokstaven Δ ("delta") och är i sin tur en vektor. Dess enheter i det internationella systemet är mätare.

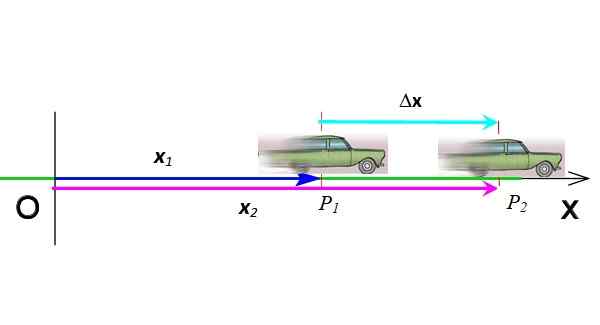Figur 3. Vektorförskjutning. Källa: Utarbetad av F. Zapata.

Vektorer betecknas med djärvt i tryckt text. Men att vara på samma dimension, om så önskas kan du klara dig utan vektorotationen.

Kan tjäna dig: grenar av klassisk och modern fysik

Distans rest

Distans d Turnerad av det rörliga objektet är det absoluta värdet på förskjutningsvektorn:

D = OderxΙ = Δx

Som ett absolut värde är avståndet alltid större än eller lika med 0 och dess enheter är desamma som position och förskjutning. Absolut värde -notation kan göras med modulstänger eller helt enkelt ta bort den djärva bokstaven i tryckt text.

Medelhastighet

Hur snabbt förändras positionen? Det finns långsamma och snabba mobiltelefoner. Nyckeln har alltid varit hastigheten. För att analysera denna faktor analyseras positionen x tidsfunktion t.

Medelhastigheten v_m (Se figur 4) Det är lutningen för torklinjen (fuchsia) till kurvan x mot t och ger global information om mobilförskjutning i det tidsintervallet som beaktas.

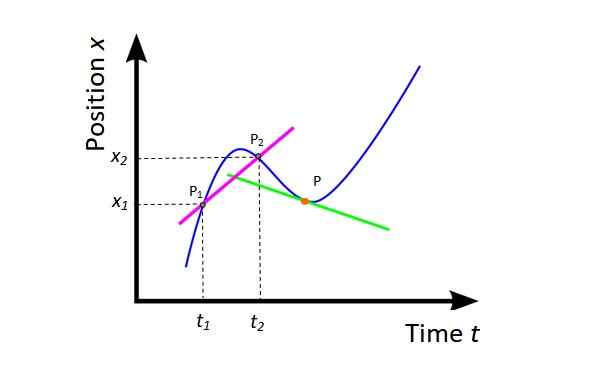Figur 4. Medelhastighet och omedelbar hastighet. Källa: Wikimedia Commons, modifierad av F. Zapata.

v_m = (x₂ - x₁) / (t₂ -t₁) = 5x / 5t

Medelhastigheten är en vektor vars enheter i det internationella systemet är meter /sekund (Fröken).

Omedelbar hastighet

Medelhastigheten beräknas genom att ta ett mätbart tidsintervall, men informerar inte om vad som händer inom nämnda intervall. För att veta hastigheten när som helst måste du göra tidsintervallet mycket litet, matematiskt motsvarar det att göra:

ΔT → 0

Ekvationen ges tidigare för medelhastighet. På detta sätt erhålls den omedelbara hastigheten eller helt enkelt hastigheten:

Geometriskt är derivatet av positionen med avseende på tid lutningen på linjen tangent till kurvan x mot t vid en viss punkt. I figur 4 är punkten orange och tangentlinjen är grön. Den omedelbara hastigheten vid denna punkt är lutningen för den linjen.

Fart

Hastighet definieras som det absoluta värdet eller hastighetsmodulen och är alltid positiv (signalering, vägar och motorvägar är alltid positiva, aldrig negativa). Termen "hastighet" och "hastighet" kan användas dagligen, men i fysiken är skillnaden mellan vektor och klättring nödvändig.

v = OdervΙ = v

Genomsnittlig acceleration och omedelbar acceleration

Hastigheten kan förändras under rörelsens gång och verkligheten är att den förväntas göra det. Det finns en storlek som kvantifierar denna förändring: acceleration. Om vi ​​märker att hastigheten är förändringen av position med avseende på tid, är acceleration ändringen av hastighet med avseende på tid.

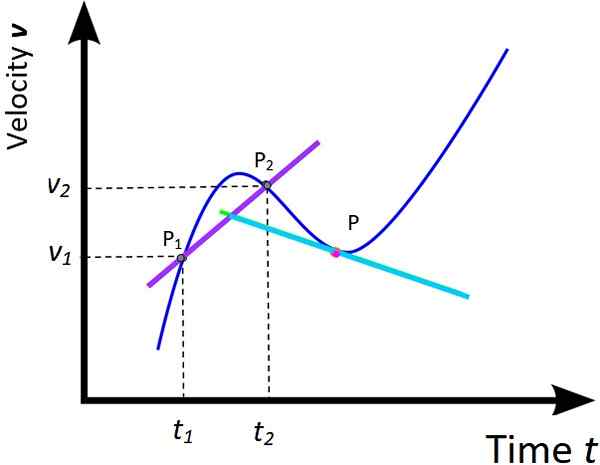Figur 5. Genomsnittlig acceleration och omedelbar acceleration. Källa: Wikimedia Commons, modifierad av F. Zapata.

Behandlingen som ges till grafen av x mot t av de två tidigare avsnitten kan utvidgas till motsvarande graf av v mot t. Följaktligen definieras en genomsnittlig acceleration och omedelbar acceleration som:

till_m = (v₂ - v₁) / (t₂ -t₁) = 5v / 5t  (I väntan på bostaden)

Acceleration och retardation

I en -dimensionell rörelse har vektorer efter konvention positiva eller negativa tecken när de går på ett eller annat sätt. När accelerationen har samma betydelse som hastigheten ökar det dess storlek, men när det är motsatt förnuft och hastigheten minskar dess storlek. Det sägs då att rörelsen är försenad.

Kan tjäna dig: Leyden -flaska: delar, drift, experiment

Grabbar

Klassificeringen av rektilinesiska rörelser görs vanligtvis baserat på:

- Huruvida accelerationen är konstant eller inte.

- Rörelsen passerar längs en horisontell eller vertikal linje.

Rörelse med konstant acceleration

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

När accelerationen är konstant, den genomsnittliga accelerationen till_m Det är lika med omedelbar acceleration till Och det finns två alternativ:

- Att accelerationen är värd 0, i vilket fall hastigheten är konstant och har en enhetlig rätlinjig rörelse eller MRU.

- Konstant acceleration skiljer sig från 0, där hastigheten växer eller minskar linjärt över tid (den rätlinjiga rörelsen enhetligt varierad eller MRUV):

Var v_F  och t_F De är slutliga hastighet respektive tid, och v_antingen och t_antingen De är initial hastighet och tid. Ja t_antingen = 0, När du rensar den slutliga hastigheten har du ekvationen som redan är bekant för den slutliga hastigheten:

v_F = v_antingen + PÅ

För denna rörelse är följande ekvationer också giltiga:

- Position beroende på tid: x = x_antingen + v_{antingen .}t +½ at²

- Hastighet beroende på position: v_F² = v_antingen² + 2: a.Δx  (Med Δx = x - x_antingen)

Horisontella rörelser och vertikala rörelser

De horisontella rörelserna är de som passerar längs den horisontella axeln eller x -axeln, medan de vertikala gör det längs axeln och axeln. Vertikala rörelser under tyngdkraften är de vanligaste och intressanta.

I de tidigare ekvationerna tas det A = g = 9.8 m/s² riktad vertikalt ner, riktning som nästan alltid väljs med ett negativt tecken.

Den här vägen, v_F = v_antingen + PÅ Det förvandlas in v_F = v_antingen - Gt Och om den initiala hastigheten är 0 eftersom objektet tappades fritt, förenklas det ytterligare till v_F = - GT. Så länge luftmotståndet inte beaktas, naturligtvis.

Löst exempel

Exempel 1

Vid punkt A släpps ett litet paket så att det rör sig längs transportören med skjuthjul ABCD som visas i figuren. Medan de faller ner genom de lutande sektionerna AB och CD, har paketet en acceleration på 4,8 m/s², Medan det är i det horisontella avsnittet BC upprätthåller konstant hastighet.

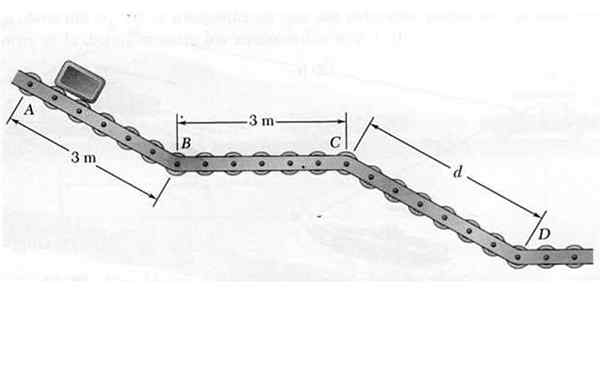Figur 6. Paketet som rör sig på glidbanan för det lösta exemplet 1. Källa: Självgjord.

Att veta att hastigheten med vilken paketet vid D når är 7,2 m/s, bestäm:

a) Avståndet mellan C och D.

b) den tid som krävs för att paketet ska nå slutet.

Lösning

Paketets rörelse utförs i de tre rätlinjiga sektionerna som visas och för att beräkna den begärda krävs hastigheten vid punkterna B, C och D. Låt oss analysera varje avsnitt separat:

Sektion AB

Eftersom tiden inte är tillgänglig i det här avsnittet kommer det att användas v_F² = v_antingen² + 2: a.Δx  Med vo = 0:

v_F² = 2a.Δx → v_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/s² → v_F  = 5.37 m/s = v_B

Den tid som paketet tar för att resa avsnittet AB är:

t_Ab = (v_F - v_antingen) /A = 5.37 m/s/4,8 m/s² = 1.19 s

Avsnitt BC

Hastigheten i avsnitt BC är därför konstant v_B = v_C = 5.37 m/s. Den tid det tar för paketet att resa detta avsnitt är:

Kan tjäna dig: Lätt brytning: Element, lagar och experiment

t_{före Kristus} = avstånd _{före Kristus}  / v_B = 3 m/ 5.37 m/s = 0.56 s

Cd -sektion

Den första hastigheten för detta avsnitt är v_C = 5.37 m/s, Den slutliga hastigheten är v_D = 7,2 m/s, via v_D²  = v_C² + 2. till. d Värdet av d:

D = (v_D²  - v_C²)/2.A = (7.2²  - 5.37²)/2 x 4.8 m = 2.4 m

Tiden beräknas som:

t_{CD =} (v_D  - v_C)/A = (7.2- 5.37)/ 4.8 s = 0.38 s.

Svaren på de frågor som ställs är:

a) D = 2.4 m

b) restiden är t_Ab + t_{före Kristus} + t_CD = 1.19 s +0.56 S +0.38 s = 2.13 s.

Exempel 2

En person är under en horisontell grind som ursprungligen är öppen och 12 m hög. Personen lanserar vertikalt ett föremål mot grinden med 15 m/s hastighet.

Det är känt att porten stänger 1,5 sekunder efter att personen har lanserat föremålet från en höjd av 2 meter. Luftmotstånd kommer inte att beaktas. Svara på följande frågor och motivera:

a) lyckas du passera objektet genom grinden innan den stängs?

b) Kommer objektet någonsin att kollidera mot den stängda grinden? Om det är bekräftande, när händer det?

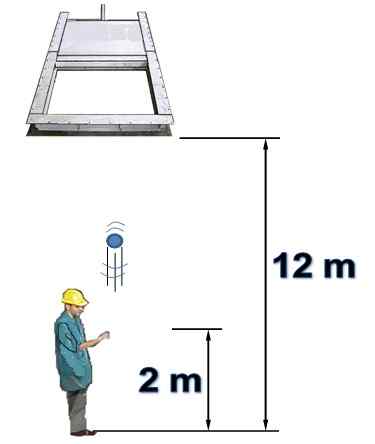Figur 7. Ett objekt lanseras vertikalt upp (löst exempel 2). Källa: Självgjord.

Svara på)

Det finns 10 meter mellan bollens initiala läge och grinden. Det är en vertikal lansering, där denna adress tas som positiv.

Du kan ta reda på den hastighet som den bär när du anländer till denna punkt, med detta resultat den tid det skulle ta att göra det och jämföra den med portens sluttid, vilket är 1.5 sekunder:

v_F ²= v_antingen ²- 2.g. Δoch → v_F = (15² - 2 x 9.8 x10)^1/2 M = 5.39 m/s

T = (V_F - v_antingen) /g = (5.39 - 15) / (-9.8) s = 0.98 s

Eftersom denna tid är mindre än 1.5 sekunder, då dras slutsatsen att objektet kan gå igenom grinden minst en gång.

Svar B)

Vi vet redan att objektet hanterar. Hastigheten, när den når vid portens höjd har samma storlek som när den går upp, men i motsatt riktning. Arbeta därför med -5.39 m/s och den tid det tar att nå denna situation är:

T = (V_F - v_antingen) /G = (-5.39 - 15) / (-9.8) s = 2.08 s

Eftersom porten förblir öppen endast för 1.5 s, det är uppenbart att det inte har tid att passera innan den stängs, eftersom den finner den stängd. Svaret är: objektet om det kolliderar med den stängda grinden efter 2.08 sekunder efter att ha släppts, när den kommer i nedstigning.

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB).69-116.
2. Giancoli, D. Fysik. (2006). Principer med applikationer. 6^th Utgåva. Prentice hall. 22-25.
3. Kirkpatrick, l. 2007. Fysik: En titt på världen. 6^ta Förkortad upplaga. Cengage Learning. 23 - 27.
4. Resnick, r. (1999). Fysisk. Volym 1. Tredje upplagan på spanska. Mexiko. Kontinentala redaktionella företag s.TILL. av C.V. 21-22.
5. Rex, a. (2011). Fysikens grunder. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14^th. Ed. Volym 1. 50 - 53.
7. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7^ma. Utgåva. Mexiko. Cengage Learning Editors. 23-25.
8. Serway, R., Vule, c. (2011). Fysikens grunder. 9^na Ed. Cengage Learning. 43 - 55.
9. Wilson, J. (2011). Fysik 10. Pearson Education. 133 - 149.