Enhetligt accelererade rätlinjer rörelseegenskaper, formler

han enhetligt accelererad rätlinjär rörelse Det är den som passerar över en rak linje och där mobilen ökar eller minskar sin hastighet med en konstant hastighet. Denna hastighet är den storlek som beskriver rytmen med vilken hastighet förändras och kallas acceleration.

När det gäller den enhetligt accelererade eller varierade rätlinjiga rörelsen (MRUV) är konstantaccelerationen ansvarig för att ändra hastighetens storlek. I andra typer av rörelse kan acceleration också ändra riktningen och känslan av hastighet, eller till och med ändra riktningen, som i den enhetliga cirkulära rörelsen.

Figur 1. Accelererade rörelser är de vanligaste. Källa: Pixabay.

Eftersom accelerationen representerar hastighetsförändringen över tid är dess enheter i det internationella systemet m/s² (meter på sekunder kvadrat). Som hastighet kan acceleration tilldelas positivt eller negativt tecken, eftersom hastigheten ökar eller minskar.

En acceleration säger om +3 m/s² Det betyder att för varje sekund som passerar ökar mobilhastigheten med 3 m/s. Om den mobila hastigheten i början av rörelsen (vid t = 0) var +1 m/s, kommer den efter en sekund att vara 4 m/s och efter 2 sekunder kommer den att vara 7 m/s.

I den jämnt varierade rätlinjiga rörelsen beaktas de hastighetsvariationer som mobila objekt dagliga erfarenheter beaktas. Det är en mer realistisk modell än den för den enhetliga rätlinjiga rörelsen. Fortfarande är det fortfarande ganska begränsat, eftersom den begränsar mobilen för att bara resa på en rak linje.

[TOC]

Egenskaper

Dessa är de viktigaste egenskaperna hos den enhetligt accelererade rätlinjiga rörelsen:

-Rörelsen passerar alltid en rak linje.

-Accelerationen av mobilen är konstant, både i storlek och i riktning och mening.

-Mobilhastigheten ökar (eller minskar) linjär.

-Sedan accelerationen till förblir konstant över tiden t, Grafen av dess storlek som en funktion av tiden är en rak linje. I exemplet som visas i figur 2 är linjen blå och accelerationsvärdet läses på den vertikala axeln, ungefär +0.68 m/s².

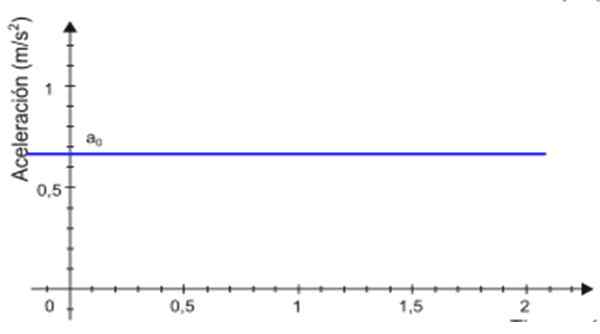figur 2. Accelerationsgraf enligt tiden för en enhetlig varierad rätlinjig rörelse. Källa: Wikimedia Commons.

-Hastighetsdiagrammet v handla om t Det är en rak linje (i grönt i figur 3), vars lutning motsvarar mobil acceleration. I exemplet är lutningen positiv.

Det kan tjäna dig: Boron Nitride (BN): Struktur, egenskaper, erhållning, användning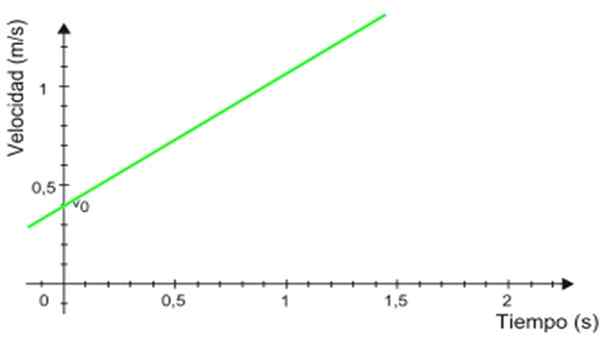 Figur 3. Hastighetsgraf baserad på tid för en enhetligt varierad rätlinjig rörelse. Källa: Wikimedia Commons.

-Snittet med den vertikala axeln indikerar den initiala hastigheten, i detta fall är det 0.4 m/s.

-Slutligen är grafen för X -positionen kontra tid den kurva som visas i rött i figur 4, som alltid är en liknelse.

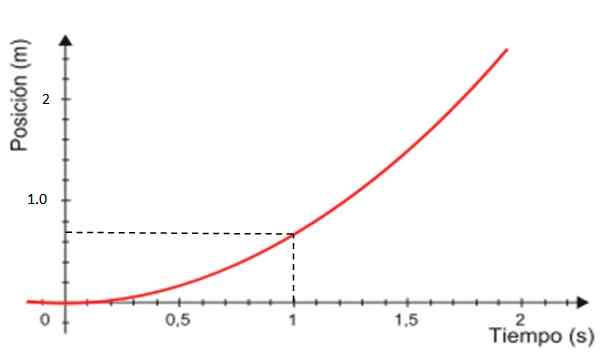Figur 4. Grafik över positionen baserad på tid för en enhetligt varierad rätlinjig rörelse. Källa: Modifierad Wikimedia Commons.

Avstånd som reste från graf V vs. t

Genom att ha graf v vs. t, beräkningen av det avstånd som röret har kört är mycket enkelt. Det resade avståndet motsvarar området under linjen som ingår i önskat tidsintervall.

I exemplet som visas, anta att du vill veta det avstånd som mobilen har kört mellan 0 och 1 sekund. Genom att använda denna graf, se figur 5.

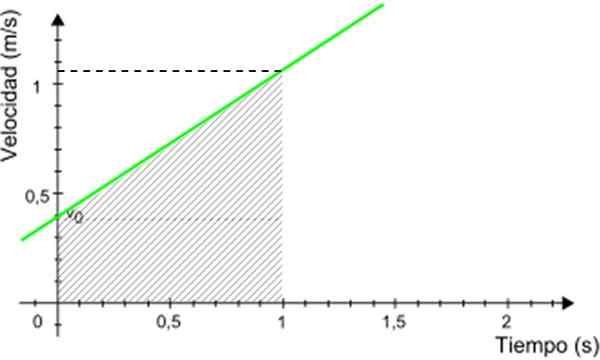Figur 5. Graf för att beräkna det avstånd som går av mobilen. Källa: Modifierad Wikimedia Commons.

Avståndet som sökts numeriskt motsvarande området med skuggad trapezoid i figur 3. Trapezoidområdet ges av: (Större bas + mindre bas) x höjd/2

Rest avstånd = (0.4 + 1.05) x 1/2 m = 0.725 m

Det är också möjligt att dela upp det skuggade området i en triangel och en rektangel, beräkna motsvarande områden och lägga till dem. Det resade avståndet är positivt, även om partikeln går till höger eller till vänster.

Formler och ekvationer

Både genomsnittlig acceleration och omedelbar acceleration har samma värde i MRUV därför:

-Acceleration: till = konstant

När accelerationen är lika med 0 är rörelsen enhetlig rätlinjig, eftersom hastigheten skulle vara konstant i detta fall. Tecknet på till Det kan vara positivt eller negativt.

Eftersom accelerationen är lutningen för linjen V kontra t är ekvation V (t):

-Hastighet beroende på tid: v (t) = v_antingen + PÅ

Var v_antingen Det är det ursprungliga mobilhastighetsvärdet

-Position beroende på tid: x (t) = x_antingen + v_antingen T +½at² 

När tiden inte är tillgänglig, men istället finns det hastigheter och förskjutningar finns det en mycket användbar ekvation som erhålls genom att rensa tiden för v (t) = v_antingen + PÅ och ersätta den i den sista ekvationen. Är om:

Kan tjäna dig: Potentiell energi: Egenskaper, typer, beräkning och exempel

-Ekvation som inte innehåller tid: v² = v_antingen² +2.till.Δx

Löst övningar

Vid lösning av en kinematikövning är det viktigt att se till att de föreslagna situationen anpassar sig till modellen som ska användas. Till exempel är ekvationerna för den enhetliga rätlinjiga rörelsen inte giltiga för en accelererad rörelse.

Och de från den accelererade rörelsen är inte giltiga för en cirkulär eller kröklig rörelse, till exempel. Den första av dessa övningar som löses nedan kombinerar två mobiler med olika rörelser. För att lösa det korrekt är det nödvändigt att gå till lämplig rörelsemodell.

-Motion Löst 1

För att ta reda på djupet på en brunn tappar ett barn ett mynt och aktiverar samtidigt sitt stoppur, som stannar exakt när du lyssnar på valutakuppet mot vatten. Läsningen var 2.5 sekunder. Att veta att ljudets hastighet i luften är 340 m/s, beräkna djupet på brunnen.

Lösning

Vara h Brunnens djup. Valutan reser detta avstånd i fritt fall, en enhetligt varierad vertikal rörelse, med initial hastighet 0, eftersom valutan tappas och konstant acceleration ner samma som 9.8 m/s². Ta en tid t_m Genom att göra detta.

När valutan kolliderar med vatten reser ljudet som orsakas av klicket upp till barnets öra, som stoppar stoppur när man lyssnar på det. Det finns inga skäl att tro att ljudets hastighet förändras när du klättrar brunnen, så ljudrörelsen är enhetlig rätlinjig. Ljudet tar tid t_s för att nå barnet.

Rörelsekvation för valutan:

H = ½.g.t_m ² = 4.9 T_m ²

Där de har ersatts x och till av ekvationen för den position som anges i föregående avsnitt, av h och g.

Ljudrörelseekvation:

h = v_s . t_s = 340 t_s

Detta är den bekanta ekvationen Avstånd = hastighet x tid. Med dessa två ekvationer finns det tre okända: H, TM och TS. I tider finns det en relation, det är känt att allt tar 2.5 sekunder i händer därför:

t_m + t_s = 2.5 s

Utjämna båda ekvationerna:

4.9 T_m ² = 340 t_s

Rensa en av tiderna och ersätta:

4.9 T_m ²= 340.(2.5 - T_m)

När man utvecklar termen för rätt och transponering av termer erhålls det:

Kan tjäna dig: vertikalt skott: formler, ekvationer, exempel

4.9 T_m ²+340 t_m - 850 = 0

Detta är en andra gradsekvation med två lösningar: 2.416 och -71.8. Den positiva lösningen väljs, vilket är den som är vettigt, eftersom tiden inte kan vara negativ och i alla fall måste den vara mindre än 2.5 sekunder. För denna tid erhålls det genom att ersätta djupet i brunnen:

4.9 T_m ²= 4.9 x 2.416² M = 28.6 m

-Motion Löst 2

En bil som reser vid 90 km/h närmar sig en tvärgående väg med trafikljus. När det är 70 m där är det gula ljuset på, vars varaktighet är 4 sekunder. Avståndet mellan trafikljuset och nästa hörn är 50 m.

Föraren har dessa två alternativ: a) Stå på - 4 m/s² eller b) accelerera vid + 2 m/s². Vilka av de två alternativen gör det möjligt för föraren att stoppa eller korsa hela vägen innan ljuset ändras till rött?

Lösning

Förarens ursprungliga position är x = 0 precis när han ser det gula ljuset. Det är viktigt att konvertera enheterna ordentligt: ​​90 km/h är lika med 25 m/s.

Enligt alternativ A), på de fyra sekunderna att det gula ljuset varar föraren reser:

x (t) = v_antingen T +½at²= 25.4 -½.(-4).4²M = 68 m (2 meter innan trafikljuset)

Analysera alternativ B) Du har:

x (t) = v_antingen T +½at²= 25.T +½.2.t²

Medan det gula ljuset varar, reser föraren på detta sätt:

x = 25.4 +½.2.4²M = 116 m

Men 116 m är mindre än det tillgängliga avståndet för att nå nästa hörn, vilket är 70 + 50 m = 120 m, därför misslyckas det att korsa hela gatan innan det röda ljuset är på. Den rekommenderade åtgärden är att stoppa och stanna 2 meter från trafikljuset.

Ansökningar

Varje dag upplever människor effekterna av acceleration: när de reser med bil eller buss, eftersom de ständigt behöver stoppa och accelerera för att anpassa marschen till vägens hinder. Acceleration upplevs också när den går upp eller ner i en hiss.

Roliga parker är platser där människor betalar för att uppleva effekterna av acceleration och ha kul.

I naturen observeras den enhetligt varierade rätlinjiga rörelsen när ett objekt tappas fritt, eller när det kastas vertikalt upp och förväntas återvända till marken. Om luftmotståndet föraktas är värdet på accelerationen tyngdkraften: 9.8 m/s2.

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.40-45.
2. Figueroa, D. Fysisk serie för vetenskap och teknik. Volym 3. Utgåva. Kinematik. 69-85.
3. Giancoli, D.  Fysik: Principer med applikationer. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Konceptuell fysisk vetenskap. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, l. 2007. Fysik: En titt på världen. 6^ta Förkortad upplaga. Cengage Learning. 15-19.
6. Wilson, J. 2011. Fysik 10. Pearson Education. 116-119