han Algebraisk balansmetod Det används i kemi för att matcha antalet atomer på båda sidor av en kemisk reaktion. En kemisk reaktion skriven korrekt, måste ha formlerna för alla reagens som deltar på vänster sida och produkterna, även med sina formler, på höger sida.

Men när du har en reaktion är antalet atomer i formlerna för reagensen lika med respektive atomer i formlerna för produkterna inte alltid.

Figur 1. Algebraisk balanseringsmetod är ett enkelt verktyg för att balansera kemiska ekvationer. Källa: f. Zapata.

Degen bevaras dock. Låt oss till exempel se följande reaktion:

KCl₃ → kcl + o₂

Denna ekvation har en förening som kallas kaliumklorat, som bryts ned genom uppvärmning i kaliumklorid och gas syre. Men när vi tittar noggrant, märker vi att i kloratmolekylen finns det 3 syreatomer, medan det till höger bara finns en gas syremolekyl med 2 atomer.

Det som då görs är att multiplicera med en numerisk koefficient till vänsterens reagens, så att antalet atomer i alla deltagande element är detsamma före och efter reaktionen.

Men ... vad är värdet på denna koefficient?

[TOC]

Sätt att balansera ekvationer

I föregående ekvation är det lätt att bestämma lämpliga koefficienter genom inspektion. Om vi ​​multiplicerar med 2 till vänster har vi 2 atomer av K, 2 av Cl och 6 av O.

Därför multiplicerar vi till höger kaliumkloriden med 2 och O₂ med 3:

2 kclo₃ → 2KCl + 3O₂

Och nu kan vi se att redovisningen är korrekt på båda sidor av pilen och reaktionen var balanserad. Observera att andra numeriska värden också kan resultera i en balanserad ekvation, till exempel:

Kan tjäna dig: Borsyran: Kemisk struktur, egenskaper, beredning, användningar

4 kclo₃ → 4KCl + 6o₂

Uppsättningen av hela minimumantal som är lika med mängden atomer på båda sidor bör emellertid alltid sökas.

Siffrorna som multiplicerar varje formel kallas koefficienter. Det är mycket viktigt att notera att koefficienter kan tilldelas att balansera, men abonnemang måste förbli som de visas i varje formel.

Koefficienter kan inte heller sättas in i mitten av formeln för varje förening, eftersom den skulle förändra den.

Enkla ekvationer som exempel kan balanseras genom inspektion eller poäng. För de som är lite mer komplexa finns det en algebraisk metod med en serie enkla steg och elementära aritmetiska operationer som beskrivs nedan.

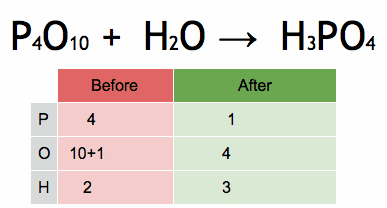figur 2. Animering som visar balanseringen av en kemisk ekvation för att erhålla fosforsyra. Källa: Wikimedia Commons. Efert/CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/4.0)

Steg för att algebraiskt balansera en kemisk ekvation

Steg 1

-Tilldela varje molekyl en godtycklig koefficient, symboliserad av en bokstav. Lyrics A, B, C, D .. ., vid behov vid behov.

Viktig: Kom ihåg att endast en koefficient används av molekylen och aldrig är isär mitt i den, den är alltid placerad till vänster.

Steg 2

-Gör en lista över varje deltagande element.

Steg 3

-Placera koefficienten eller koefficienterna tilldelade varje förening till vänster och matcha de till höger. Om det finns abonnemang multiplicerar de med koefficienten för att hitta det totala antalet atomer.

Och om något element finns i mer än en molekyl, läggs mängder av atomer som finns på varje sida. På detta sätt partiella ekvationer av varje element.

Steg 4

-Ett numeriskt värde tilldelas en av koefficienterna. Vanligtvis är detta numeriska värde 1 och tilldelas bokstaven som visas fler gånger. Detta uppnår en enkel ekvation som fungerar som en utgångspunkt för att hitta de andra koefficienterna.

Kan tjäna dig: utspädningsfaktor

Steg 5

-Bestäm värdet på följande koefficient med enkel aritmetik och ersätt dess värde i en annan ekvation, för att höja en ny.

Steg 6

-Upprepa föregående steg för att ersätta värden och skapa en ny ekvation tills du hittar alla koefficienter.

Steg 7

-Byt ut värden som således bestäms. Om dessa värden är hela måste det verifieras att ekvationen var balanserad. Om de inte var hel, multipliceras det med den minsta gemensamma multipeln av nämnaren och balansen kontrolleras.

Sedan kommer vi att visualisera tillämpningen av dessa steg i upplösningen av några exempel.

Löst balanseringsexempel

Exempel 1

Balansera följande reaktion vid behov, genom den algebraiska metoden:

N₂ANTINGEN₅ → n₂ANTINGEN₄ + ANTINGEN₂

Lösning

Vi observerar att reaktionen inte är balanserad, för även om det finns 2 kväveatomer på båda sidor, med syre är mängderna till vänster och höger olika.

Då måste vi följa stegen som beskrivs i föregående avsnitt:

-Vi skriver ekvationen igen och multiplicerar varje molekyl med en annan koefficient. Små bokstäver väljs så att de inte är förvirrade med elementen:

A⋅n₂ANTINGEN₅ → B⋅n₂ANTINGEN₄ + Cara₂

-Nu listar vi varje element och matchar mängderna för det elementet till vänster och höger. Dessa är de partiella ekvationerna för varje element:

1. A⋅n₂ = B⋅n₂
2. A⋅o₅ = B⋅o₄ + Cara₂

-Multiplicera koefficienten och abonnemanget får vi antalet kväveatomer. Från ekvation 1 får vi:

2a = 2b

-Av ekvation 2 har Femte Syreatomer till vänster, medan till höger finns det 4B och 2 c:

5a = 4b + 2c

-Vi tilldelar värde 1 till koefficient A, på detta sätt:

A = 1

Detta val är godtyckligt, det kan också väljas först b = 1.

-Dessa värden ersätts i ekvation 2 för att bestämma värdet på C:

Det kan tjäna dig: Cupric Oxide (CUO)

5 = 4 + 2c

2c = 5-4 = 1

C = ½

-Vi ersätter koefficienterna i den ursprungliga ekvationen, 1 är inte nödvändig för att skriva den uttryckligen:

N₂ANTINGEN₅ → n₂ANTINGEN₄ + ½ o₂

-Eftersom det är att föredra att koefficienterna är hel, multipliceras hela ekvationen med den minsta gemensamma multipeln av nämnaren, som är 2 och 1:

m.c.m. (1.2) = 2

Sedan, genom att multiplicera vänster och höger med 2, erhålls det:

2n₂ANTINGEN₅ → 2n₂ANTINGEN₄ + ANTINGEN₂

Och vi räknar antalet atomer på båda sidor för att kontrollera balansen:

• N till vänster: 4
• Eller vänster: 10
• N till höger: 4
• Eller höger: 8 + 2 = 10

Exempel 2

Balansera följande kemiska reaktion:

Nahco₃ → Na₂Co₃ + H₂Eller + co₂

Lösning

Vi multiplicerar varje molekyl med en annan koefficient:

A⋅ nahco₃ → b⋅na₂Co₃ + C⋅h₂O + d⋅co₂

Sedan föreslår vi redovisningen av varje element till höger och till vänster om pilen. Det finns totalt fyra element i reaktionen: natrium Na; Väte H; bilbil och syre eller alla måste räknas:

• A⋅na = b⋅na₂
• a⋅h = c⋅h₂
• A⋅C = B⋅C + D⋅C
• A⋅o₃ = B⋅o₃+C⋅O+D⋅O₂

Enligt varje balans erhålls följande ekvationer:

1) a = 2b
2) A = 2C
3) a = b + d
4) A = 3B + C + 2D

Den mest upprepade koefficienten är till, Därför tilldelar vi värdet 1:

A = 1

Så:

1) A = 2B ⇒ B = ½
2) a = 2c ⇒ c = ½
3) A = B + D ⇒ D = A - B = 1 - ½ = ½

Vi ersätter koefficienterna i ekvationen:

Nahco₃ → ½. Na₂Co₃ + ½. H₂O + ½.Co₂

Vi multiplicerar på båda sidor av pilen med 2, eftersom det är den enda nämnaren som är närvarande, som eliminerar fraktionen:

2nahco₃ → Na₂Co₃ +  H₂Eller + co₂

Vi räknar antalet atomer närvarande till vänster: 2 atomer av Na, H och C och 6 av O. Läsaren kan verifiera att var och en av dem också är närvarande till höger i samma mängder.

Referenser

1. Atkins, s. Principer för kemi: upptäcktsvägarna. Pan -American Medical Redaktion. 3: e upplagan.
2. Briceño, J. USB -kemi -guide. Återhämtat sig från: gecousb.com.gå.
3. Chang, R. 2013. Kemi. 11VA. Utgåva. MC Graw Hill Education.
4. Löst övningar. Algebraisk balansering. Hämtad från: Suelted -övningar.co.
5. Simoza, L. Balansering av kemiska ekvationer. Återhämtat sig från: guao.org.