Irrationella siffror historia, egenskaper, klassificering, exempel

De irrationella siffror De är de vars decimaluttryck har oändliga figurer utan ett repetitivt mönster, därför kan de inte erhållas genom att göra kvoten mellan två heltal.

Bland de mest kända irrationella siffrorna är:

Figur 1. Från topp till botten följande irrationella nummer: Pi, antalet Euler, Aúrea och två kvadratrötter. Källa: Pixabay.

Bland dem är utan tvekan π (pi) det mest bekanta, men det finns många fler. Alla tillhör uppsättningen verkliga siffror, som är den numeriska uppsättningen som förenar rationella och irrationella siffror.

De suspensiva punkterna i figur 1 indikerar att decimalerna följer på obestämd tid, vad som händer är att utrymmet för de nuvarande kalkylatorerna bara tillåter att visa några få.

Om vi ​​tittar noggrant, förutsatt att vi gör kvoten mellan två heltal, erhålls en decimal med begränsade siffror eller om inte, med oändliga siffror där en eller flera de upprepas. Tja, detta händer inte med irrationella siffror.

[TOC]

Irrationellt siffror

Den stora matematikern av antiken Pythagoras, född 582 till.C i Samos, Grekland, grundade Pythagorean School of Thought och upptäckte den berömda satsen som bär hans namn. Vi har det ner till vänster (babylonierna kunde redan känna honom långt innan).

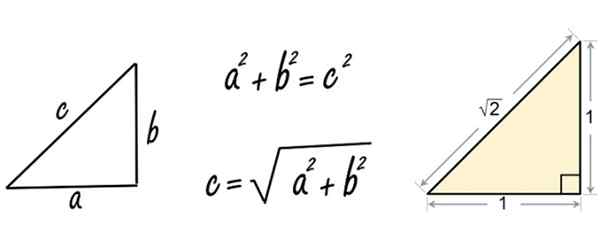figur 2. Pythagoras teorem applicerat på en triangel av sidor lika med 1. Källa: Pixabay/Wikimedia Commons.

Tja, när Pythagoras (eller förmodligen en lärjunge av hans) tillämpade teoremet på en höger triangel av sidor lika med 1, hittade det irrationella antalet √2.

Det kan tjäna dig: torklinjer

Han gjorde det på det här sättet:

C = √1² + 1² = √1+1 = √2

Och han insåg genast att detta nya nummer inte kom från kvoten mellan två andra naturliga siffror, som var de som var kända vid den tiden.

Därför kallade han honom irrationell, Och upptäckten orsakade stor ångest och förvirring bland pytagoreanerna.

Irrationella siffrans egenskaper

-Uppsättningen av alla irrationella siffror betecknas med bokstaven i och ibland gillar Q* eller Q^C. Förbundet mellan irrationella siffror I eller Q* och rationella siffror Q, ger upphov till uppsättningen verkliga n -nummer.

-Med irrationella siffror kan kända aritmetiska operationer utföras: summa, subtraktion, multiplikation, uppdelning, potentiering och mer.

-Divisionen mellan 0 är inte definierad bland irrationella siffror.

-Summan och produkten mellan irrationella siffror är inte nödvändigtvis ett annat irrationellt antal. Till exempel:

√2 x √8 = √16 = 4

Och 4 är inte ett irrationellt antal.

-Summan av ett rationellt antal plus en irrationell en resulterar dock i en irrationell. Den här vägen:

1 + √2 = 2.41421356237 ..

-Produkten av ett annat rationellt antal från 0 med ett irrationellt antal är också irrationell. Låt oss titta på det här exemplet:

2 x √2 = 2.828427125 ..

-Det inversa av ett irrationellt resultat i ett annat irrationellt antal. Låt oss prova några:

1 / √2 = 0.707106781 ..

1 / √3 = 0.577350269 ..

Dessa siffror är intressanta eftersom de också är värdena på vissa trigonometriska skäl till kända vinklar. Mycket av de trigonometriska skälen är irrationella siffror, men det finns undantag, till exempel sen 30º = 0.5 = ½, vilket är rationellt.

-I summan uppfylls de kommutativa och associativa egenskaperna. Om A och B är två irrationella siffror, betyder det att:

Kan tjäna dig: överjektiv funktion: definition, egenskaper, exempel

A + B = B + A.

Och om C är ett annat irrationellt antal, då:

(A + B) + C = A + (B + C).

-Distributivegenskapen för multiplikation med avseende på summan är en annan känd egenskap som också uppfylls för irrationella siffror. I detta fall:

till.(b+c) = a.b + a.c.

-En irrationell till har sitt motsats: -A. När resultatet läggs till är det 0:

A+(-a) = 0

-Mellan två olika rationella finns det åtminstone ett irrationellt antal.

Plats för ett irrationellt nummer på den verkliga linjen

Den verkliga linjen är en horisontell linje där de verkliga siffrorna finns, varav de irrationella är en viktig del.

För att hitta ett irrationellt nummer på den verkliga linjen, i en geometrisk form, kan vi vara värda Pythagoras teorem, en regel och en kompass.

Som ett exempel kommer vi att hitta √5 på den verkliga linjen, för vilken vi ritar en rektangel triangel av sidor x = 2 och y = 1, Som bilden visar:

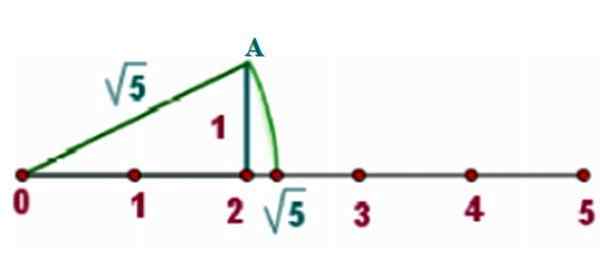Figur 3. Metod för att hitta ett irrationellt nummer på den verkliga linjen. Källa: f. Zapata.

För Pythagoras teorem är hypotenusen av en sådan triangel:

C = √2² + 1² = √4+1 = √5

Nu är takten med spetsen placerad i 0, där det också finns en av vertikalerna i den högra triangeln. Spetsen på kompasspennan måste vara på toppen till.

En omkretsbåge ritas som skär den verkliga linjen. Eftersom avståndet mellan mitten av omkretsen och vilken punkt som helst är radien, som är värt √5, är skärningspunkten också √5 från mitten.

Av grafen ser man att √5 är mellan 2 och 2.5. En kalkylator erbjuder oss det ungefärliga värdet av:

Kan tjäna dig: Bestämningskoefficient: Formler, beräkning, tolkning, exempel

√5 = 2.236068

Och så att bygga en triangel med lämpliga sidor, andra irrationella kan lokaliseras, till exempel √7 och andra.

Klassificering av irrationella siffror

Irrationella siffror klassificeras i två grupper:

-Algebraisk

-Transcendent eller transcendental

Algebraiska siffror

Algebraiska siffror, som kan vara irrationella eller inte, är lösningar av polynomekvationer vars allmänna form är:

till_n xⁿ + till_N-1x^N-1 + till_N-2x^N-2 +.. . +till₁x + a_antingen = 0

Ett exempel på polynomekvation är en andra gradsekvation som denna:

x³ - 2x = 0

Det är lätt att visa att det irrationella numret √2 är en av lösningarna för denna ekvation.

Transcendenta nummer

Istället uppstår transcendenta siffror, även om de är irrationella, aldrig som en lösning av en polynomekvation.

De transcendenta siffrorna som finns oftast i den tillämpade matematiken är π, för deras förhållande till omkretsen och antalet E- eller Euler -nummer, vilket är grunden för de neperiska logaritmerna.

Träning

På en svart fyrkant placeras en grå i det läge som anges i figuren. Det är känt att ytan på den svarta torget är 64 cm². Hur mycket är längden på båda rutorna?

Figur 4. Två rutor, varav sidans längd finns. Källa: f. Zapata.

Svar

Ytan på en kvadrat av sidan L är:

A = l²

Eftersom den svarta torget är 64 cm² av området måste dess sida vara 8 cm.

Denna åtgärd är densamma som Diagonalen av det gråa. Att tillämpa Pythagoras teorem på denna diagonal och komma ihåg att sidorna på en kvadrat mäter samma, kommer vi att ha:

8² = L_g² + L_g²

Där L_g Det är sidan av det gråa torget.

Därför: 2L_g² = 8²

Tillämpa kvadratrot på båda sidor av jämlikhet:

L_g = (8/√2) cm

Referenser

1. Carena, m. 2019. Matematikhandbok för preuniversitet. National University of the Coast.
2. Figuera, J. 2000. Matematik 9: e. Grad. Co-bo-utgåvor.
3. Jiménez, r. 2008. Algebra. Prentice hall.
4. Utbildningsportal. Irrationella siffror och deras egenskaper. Hämtad från: Portaleducative.netto.
5. Wikipedia. Irrationella siffror. Återhämtad från: är.Wikipedia.org.