Pentadecágono -element, klassificering, egenskaper, träning

En Pentadecmotgång Det är en platt figur byggd med femton raka segment och stängt. Denna typ av siffror kallas polygon och de heter enligt mängden sidor som har.

Triangeln, med tre sidor och det fyrkantiga, av fyra, är exempel på mycket bekanta polygoner, men polygonerna kan ha fler sidor.

Figur 1.  Regelbunden Pentagon med röda vertikaler. Källa: Wikimedia Commons.

De grundläggande elementen i pentadecágono är desamma som alla polygon, oavsett mängden sidor den har. Dessa element är:

-Sidor, vilka är de segment som utgör pentadecágono för totalt 15.

-Häckar, också 15, som är ändarna på de angränsande sidorna.

-Inre vinklar, De som bildas inom pentadecágono mellan två angränsande sidor.

-Yttre vinklar, bildades mellan ena sidan och förlängningen av en av de på varandra följande sidorna.

-Diagonaler, Linjesegmenten som går med i två icke -angränsande vertikaler.

[TOC]

Klassificering

En pentadecágono kan vara regelbunden antingen oregelbunden, beroende på storleken på deras sidor och måttet på dess inre vinklar. Om du har alla sidor och de lika inre vinklarna - Quilátero och Equiangle - är det regelbundet, som visas i figur 1, annars är den oregelbunden.

Det kan också klassificeras som konvex antingen konkav. En konkav Pentagon har en eller flera inre vinklar större än 180º, medan en alltid konvex har inre vinklar mindre än 180º. Den vanliga Pentagon är konvex.

En annan klassificeringskriterier beaktas om dess icke -konsekutiva sidor - eller deras tillägg - skärs eller inte. När de inte skärs, som i fallet med figur 1, sägs det att det är en enkel pentadecágon. Och om de är klippta är det komplext.

Det kan tjäna dig: analytisk geometri

Den vanliga Pentagon

Den vanliga Pentagon, vars sidor och inre vinklar har samma mått, är en figur av stor symmetri, eftersom följande ytterligare element definieras för de tidigare beskrivna:

-Centrum: Poängen att jämlika i vertikalerna och sidorna.

-Radio: Avståndet från centrum till en av de vanliga Pentagon -vertikalerna.

-Centralvinkel: Den som har sitt toppunkt i mitten av figuren och dess sidor passerar genom två angränsande vertikaler.

-Apotem, Det är det vinkelräta segmentet som förenar mitten av en sida med figurens centrum.

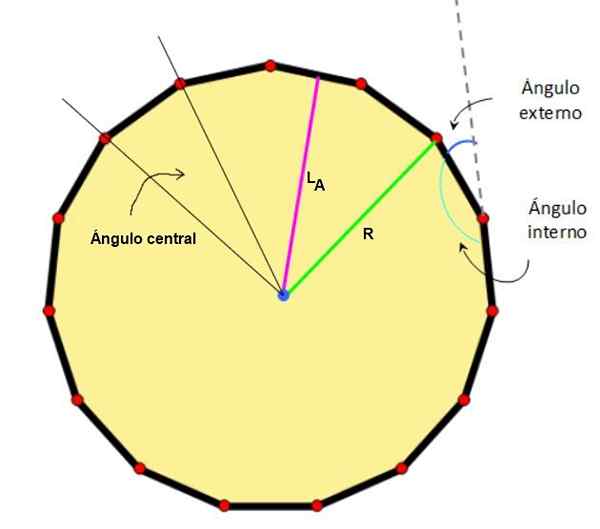figur 2. Centrum, apotem, radio och anmärkningsvärda vinklar på en pentadecágono. Källa: Wikimedia Commons/F. Zapata.

- Egenskaper för vanlig Pentagon

Inre vinklar

Följande formel används för att beräkna mått I för de inre vinklarna i någon vanlig polygon, där n Det är antalet sidor:

I den här formeln kommer åtgärden jag kommer i grader, för att uttrycka den i radianer, den multipliceras med π/180 -faktorn. Låt oss se vad som är måttet på de inre vinklarna i den vanliga Pentagon, ersätta n = 15:

I = [(15-2) × 180º]/15 = 156º

Motsvarande 13π/15 radianer. Eftersom de inre vinklarna i den vanliga Pentagon är mindre än 180º är det en konvex polygon.

Summan av inre vinklar

Det är möjligt att beräkna summan av de inre vinklarna med följande formel:

S = (n-2) x 180º

Som alltid representerar n antalet sidor. Denna formel är giltig för n = 3, 4, 5 .. .

Gör n = 15 vi får:

S = (15 - 2) x 180º = 2340º

Yttre vinklar

En inre vinkel och en yttre vinkel är kompletterande, det vill säga dess summa är 180º, som anges i figur 2. Därför en yttre vinkel på Pentadecágono -mätningen:

Kan tjäna dig: konjugerad binomial: hur det är löst, exempel, övningar

180 º - 156º = 24º.

Omkrets och område

Omkretsen är måttet på polygonkonturen och lägger lätt till alla sidor. Ja till Det är sidans längd, det räcker med att multiplicera med n, Antalet sidor.

För en regelbunden Pentagon på sidan A är omkretsen P:

P = 15a

Om det är en oregelbunden figur, där måtten på sidorna skiljer sig åt, lägger omkretsen till längden på alla sidor.

När det gäller området kan vi beräkna det på flera sätt. Till exempel har vi formeln som gör att du kan få den med att veta längden a på sidorna:

Genom att utföra de angivna operationerna förblir det ungefär:

A = 17 6426⋅a²

Det finns ett annat alternativ, tillämpligt på vanliga polygoner. Det handlar om att dela upp dem i bastrianglar som är lika med polygonen till. Triangelns höjd är längden på apotem l_TILL, definierad ovan.

Området för nämnda triangel beräknas med den välkända formeln: bas x höjd /2. På detta sätt är det enda triangelområdet:

Area = a. L_TILL /2

För att ha det totala området på polygonen räcker det att multiplicera med antalet sidor n, som i detta fall är 15:

A = 15⋅a⋅ l_TILL /2

Och eftersom figurens omkrets är p = 15⋅a, då:

A = p⋅ l_TILL /2

Diagonaler

Diagonalerna är de segment som förenar två icke -konsekutiva hörn, som anges ovan. Att veta hur många diagonaler en vanlig polygon har av n sidor, inklusive Pentadecágono, det finns följande formel:

Där D är antalet diagonaler.

Nu ersätter vi n = 15 för att få de totala diagonalerna:

Kan tjäna dig: vanliga polygoner: egenskaper, element, vinklar, exempel

D = [15 × (15-3)]/2 = 90 diagonaler.

Konstruktion med regel och kompass

Pentadecágono är byggd med regel och kompass från en omkrets. 360º måste delas upp i 15 lika delar av 24º vardera. Först utförs de hjälpskonstruktioner som anges i animationen för att få en vinkel på 60º, vilket är uppdelat i tur och ordning i 36º och 24º.

Figur 3. Konstruktion med regel och kompass av en vanlig Pentagon. Källa: Wikimedia Commons.

Träning löst

Om omkretsen av en pentadecágono registrerad i en cirkel av radie r är 12,56 cm. Beräkna:

a) radion.

b) Ditt område.

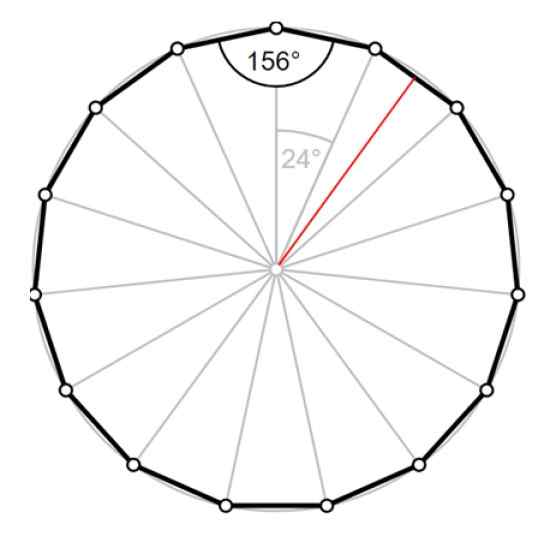Figur 4. Pentadecágono: central vinkel, inre vinkel och rött apotem. Källa: Wikimedia Commons/F. Zapata.

Lösning till

Omkretsen är p = 15⋅a = 12.56 cm därför sidan av pentadecágono är 0.8373 cm. Radion Vi kan beräkna det med hjälp av en av trianglarna i figur 4.

Apotem l_TILL motsvarar höjden på triangeln, ritad i rött, som delar vinkeln på 24º i två vinklar på 12º vardera.

Det finns två högra trianglar med en inre vinkel på 12 ° vardera, och för någon av dem kan vi applicera trigonometri för att hitta hypotenusen, vilket är radieens längd R.

Den här vägen:

Sen 12º = (a /2) /r

R = (a /2) /sen 12º = (0.8373 cm / 2) / Sen12º = 2.01 cm.

Lösning B

Vi kan beräkna Pentadecágono -området med formeln:

A = p⋅ l_TILL /2

Vi känner redan omkretsen p = 12.56 cm, och längden på apotemet beräknas av tangenten eller 12º -kosinus:

Cos 12º = l_TILL / R

L_TILL = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm

Byter ut:

A = 12.56 cm 1.97 cm /2 = 12.35 cm²

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Lär dig matematik. Geometriska figurer. Återhämtat sig från: Rodrigoanchorena.Wixsite.com.
3. Sangaku matematik. Element i en polygon och dess klassificering. Återhämtat sig från: Sangakoo.com.
4. Wikipedia. Pentadecágono. Återhämtad från: är.Wikipedia.org.
5. Wolfram matematikvärld. Pentadecagon. Återhämtat sig från: Mathworld.Volfram.com.