Icke -linjära programmeringsmetoder och övningar

De Icke -linjär programmering Det är processen att optimera en funktion som beror på flera oberoende variabler, som i sin tur är föremål för begränsningar.

Om en eller flera av begränsningarna, eller om funktionen ska maximera eller minimera (kallas Objektiv funktion), uttrycks inte som en linjär kombination av variablerna, så det finns ett icke -linjärt programmeringsproblem.

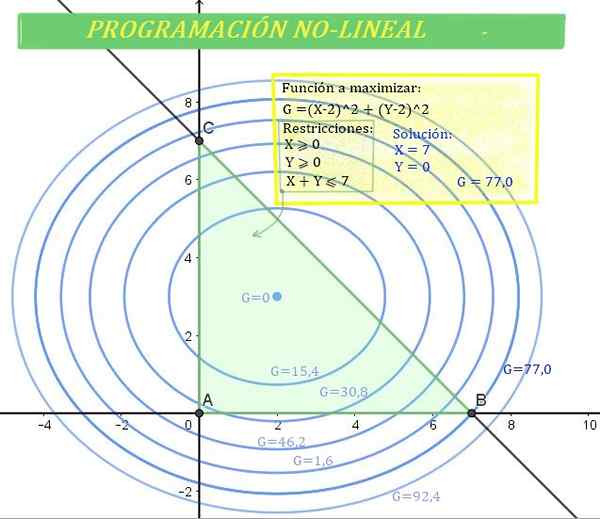
Figur 1. Icke -linjära programmeringsproblem (NLP). där g är funktionen (icke-linjär) att optimera i det gröna regionen, bestämd av begränsningarna. Källa: f. Zapata.

Och därför kan inte procedurerna och metoderna för linjär programmering användas.

Till exempel kan den välkända metoden inte användas Simplex, som endast gäller när objektivfunktionen och begränsningarna är alla linjära kombination av problemets variabler.

[TOC]

Linjära programmeringsmetoder

För icke-linjär programmering är de viktigaste metoderna som ska användas: 

1.- Grafiska metoder.

2.- Lagrange multiplikatorer för att utforska gränsen till lösningsregionen.

3.- Gradientberäkning för att utforska ändarna på objektivfunktionen.

4.- Metoden fallande steg för att hitta nollgradientpunkterna.

5.- Modifierad metod för Lagrange-multiplikatorer (med Karush-Kuhn-Tuckers skick).

Exempel på lösning med grafisk metod

Ett exempel på en lösning med den grafiska metoden är vad som kan ses i figur 2:

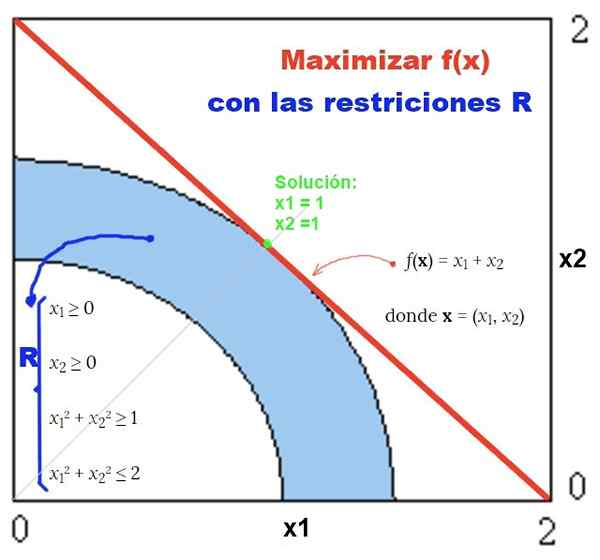figur 2. Exempel på icke-linjära problem med icke-lineala begränsningar och dess grafiska lösning. Källa: f. Zapata.

Övningar

- Övning 1 (grafisk metod)

Förstärkningen för ett visst företag beror på det sålda beloppet av produkt X och det sålda beloppet och dessutom bestäms förstärkningen av följande formel:

Kan tjäna dig: konjugerad binomial: hur det är löst, exempel, övningar

G = 2 (x - 2)² + 3 (och - 3)²

Det är känt att beloppen x och y har följande begränsningar:

X≥0; Y≥0 och x + och ≤ 7

Bestämma värdena på x och y som ger maximal förstärkning.

Figur 3. Företagets vinst kan matematiskt modelleras för att hitta den maximala förstärkningen genom icke -linjär programmering. Källa: Pixabay.

Lösning 

I detta problem är objektivfunktionen icke -linjär, medan ojämlikheterna som definierar begränsningarna är. Det är ett problem med Icke -linjär programmering.

För lösningen av detta problem kommer den grafiska metoden att väljas.

Först kommer lösningsområdet att bestämmas, som ges av begränsningarna.

Som x≥0; Y≥0, lösningen måste söka i den första kvadranten i XY -planet, men som dessutom måste den uppfyllas att X + Y ≤ 7 är lösningen i den nedre semiplanen i linjen X + Y = 7.

Lösningsområdet är skärningspunkten mellan den första kvadranten med den nedre semiplanen i linjen, vilket ger upphov till en triangulär region där lösningen är belägen. Är detsamma som anges i figur 1.

Å andra sidan kan förstärkning också representeras i det kartesiska planet, eftersom dess ekvation är en ellips med mitten (2,3).

Ellipsen visas i figur 1 för flera g -värden. Ett högre värde på G, större vinst.

Det finns lösningar som tillhör regionen, men ger inte det maximala värdet g, medan andra, till exempel g = 92.4, är utanför den gröna zonen, det vill säga lösningszonen.

Sedan motsvarar det maximala värdet på g, så att x e y tillhör lösningsregionen: 

Kan tjäna dig: Teoretisk sannolikhet: Hur man får ut det, exempel, övningar

G = 77 (maximal förstärkning), som uppstår för x = 7 e y = 0. 

Intressant nog inträffar den maximala förstärkningen när mängden produktförsäljning och är ogiltig, medan mängden produkt X når sitt största möjliga värde.

- Övning 2 (Analytisk metod: Lagrange multiplikatorer) 

Hitta lösningen (x, y) som gör funktionen f (x, y) = x² + 2 och² vara maximalt i regionen g (x, y) = x² + och² - 1 = 0.

Lösning

Det är helt klart ett icke-linjärt programmeringsproblem, eftersom både objektivfunktionen f (x, y) och begränsningen g (x, y) = 0, inte är en linjär kombination av variablerna x och y.

Lagrange -multiplikatormetoden kommer att användas, vilket först kräver att man definierar funktionen Lagrange L (x, y, λ):

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 och² - λ (x² + och² - 1) 

Där λ är en parameter som heter Lagrange multiplikator.

För att bestämma de extrema värdena för objektivfunktionen f, i lösningsområdet som ges av begränsningen g (x, y) = 0, följs dessa steg:

-Hitta de partiella derivat av Lagrange L: s funktion, med avseende på x, y, λ.

-Noll varje derivat.

Här sekvensen för dessa operationer:

1. ∂l/∂x = 2x - 2λx = 0
2. ∂l/∂y = 4y - 2λy = 0
3. ∂l/∂λ = -(x² + och² - 1) = 0

Möjliga systemlösningar

En möjlig lösning av detta system är λ = 1 för att tillfredsställa den första ekvationen, i vilket fall y = 0 för att möta den andra.

Denna lösning innebär att x = 1 eller x = -1 så att den tredje ekvationen är nöjd. På detta sätt har två S1- och S2 -lösningar erhållits:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Det andra alternativet är att λ = 2 för att den andra ekvationen ska vara nöjd, oavsett värde och.

Det kan tjäna dig: Fermat Limit: Vad består och övningar löst

I detta fall är det enda sättet för den första ekvationen att vara nöjd med att x = 0. Med tanke på den tredje ekvationen finns det bara två möjliga lösningar, som vi kommer att kalla S3 och S4:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

För att veta vilken eller vilka av dessa lösningar som maximerar den objektiva funktionen, fortsätt att ersätta i f (x, y):

S1: F (1, 0) = 1² + 2.0² = 1

S2: F (-1, 0) = (-1)² + 2.0² = 1

S3: F (0, 1) = 0² + 2.1² = 2

S4: F (0, -1) = 0² + tjugoett)² = 2

Vi drar slutsatsen att lösningarna som maximerar f, när x och y tillhör omkretsen g (x, y) = 0 är s3 och s4.

Värdenpar (x = 0, y = 1) y (x = 0, y = -1) maximera f (x, y) i lösningsregionen g (x, y) = 0.

- Övning 3 (nollgradient)

Hitta lösningar (x, y) för objektivfunktionen:

f (x, y) = x² + 2 och²

Vara maximalt i regionen g (x, y) = x² + och² - 1 ≤ 0.

Lösning

Denna övning liknar övning 2, men lösningsregionen (eller begränsningen) sträcker sig till det inre regionen i omkretsen g (x, y) = 0, det är till cirkeln g (x, y) ≤ 0. Detta inkluderar omkretsen och dess inre region.

Gränslösningen bestämdes redan i övning 2, men det är nödvändigt att utforska det inre regionen.

För att göra detta måste gradienten för funktionen f (x, y) beräknas och lika med noll för att leta efter extrema värden i lösningsregionen. Detta motsvarar att beräkna de partiella derivat av F med avseende på X respektive utjämning noll:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Detta ekvationssystem har den enda lösningen (x = 0, y = 0) som tillhör cirkel G (x, y) ≤ 0.

Ersätta detta värde i funktion f -resultat:

f (0, 0) = 0

Sammanfattningsvis är det maximala värdet som tar funktionen i lösningsområdet 2 och sker på gränsen till lösningsregionen, för värden (x = 0, y = 1) y (x = 0, y = -1).

 Referenser

1. Avriel, m. 2003. Olinjär programmering. Dover Publishing.
2. Bazaraa. 1979. Olinjär programmering. John Wiley & Sons.
3. Bertsekas, D. 1999. Icke -linjär programmering: 2: a upplagan. Athena Scientific.
4. Nocedal, J. 1999. Numerisk optimering. Kabell.
5. Wikipedia. Icke -linjär programmering. Återhämtad från: är.Wikipedia.com