Vad är kapacitiv reaktans och hur man beräknar den?

De kapacitiv reaktans Det är motståndet att en kondensor, ett reglerande element i lastflödet i en växlande strömkrets, motsätter sig passagen av strömmen.

I en krets som utgörs av en kondensator och aktiverad av en växelströmskälla kan kapacitiv reaktans X definieras_C som följer:

X_C = 1 / ωc

Figur 1. Kapacitiva reaktanser är en del av Passabajos -filter och högtalare för högtalare. Källa: Pixabay.

Eller också:

X_C = 1 / 2πfc

Där C är kondensatorns kapacitet och ω är källans vinkelfrekvens, relaterad till frekvensen f genom:

Ω = 2πf

Den kapacitiva reaktansen beror på den omvända frekvensen, därför tenderar vid höga frekvenser att vara små, medan reaktansen vid låga frekvenser är stor.

Den internationella systemenheten för att mäta den kapacitiva reaktansen är OHM (ω), förutsatt att kondensatorns kapacitet är i Farad, (förkortad F) och frekvensen uttrycks i det omvända sekunderna (S^-1).

Medan lasten varar är en spänning och en ström också etableras genom kondensatorn, vars maximala amplituder eller värden betecknas som V_C och jag_C, De är relaterade genom kapacitiv reaktans analog med Ohms lag:

V_C = Jag_C ⋅ x_C

I en kondensor försenas spänningen 90º med avseende på strömmen, eller den är avancerad 90º med avseende på det, som föredraget. I alla fall är frekvensen densamma.

När x_C Det är väldigt stort, strömmen tenderar att vara liten och göra värdet på x oändligt_C, Kondensorn uppför sig som en öppen krets och strömmen är noll.

[TOC]

Hur man beräknar kapacitiv reaktans

Låt oss titta på ett exempel på hur man beräknar den kapacitiva reaktansen: Anta att en 6 μF kondensator är ansluten till ett växelvärde och frekvens och frekvens F 60 Hz.

För att hitta den kapacitiva reaktansen används definitionen i början. Vinkelfrekvensen ω ges av:

Det kan tjäna dig: magnetisk induktion: formler, hur det beräknas och exempel

Ω = 2πf = 2π x 60 Hz = 377 s^-1

Sedan ersätts detta resultat i definitionen:

X_C = 1 / ωc = 1 / (377 s^-1x 6 x10 ^-6 F) = 442.1 ohm

Låt oss nu se amplituden för den nuvarande cirkulerande i kretsen. Eftersom källan erbjuder en amplitudspänning v_C = 40 V, vi använder förhållandet mellan kapacitiv reaktans, ström och spänning för att beräkna amplituden för den maximala strömmen eller strömmen:

Yo_C = V_C / X_C = 40 V / 442.1 ohm = 0.09047 a = 90.5 m a.

Om frekvensen blir mycket stor blir den kapacitiva reaktansen liten, men om frekvensen blev 0 och vi hade en likström, skulle reaktansen tendera att vara oändlig.

Ström- och kondensorspänning

När en kondensator ansluter till en växlande strömkälla, som den svänger och ändrar dess polaritet, upplever kondensatorn belastningar och urladdningar växelvis.

För en frekvens av 60 Hz som exemplet är spänningen positiv 60 gånger per sekund och negativ ytterligare 60 gånger per sekund.

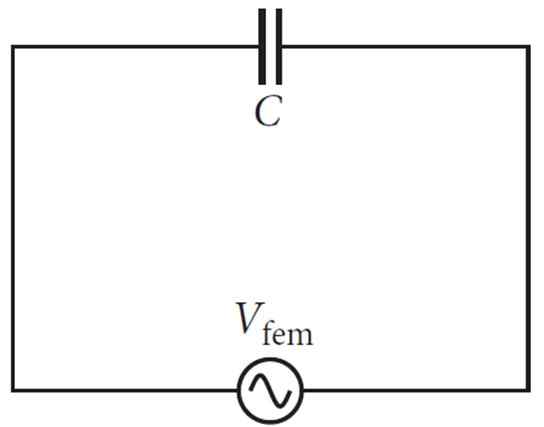
figur 2. Enkel kondensorkrets och växlande strömkälla. Källa: f. Zapata.

Genom att öka spänningen driver den strömmen i en riktning, men om kondensorn laddas ner sker strömmen i motsatt riktning som motsätter sig den första.

Ja v_C (t) = v_m Sen ωt, att veta att kapaciteten är orsaken mellan belastningen och spänningen, kommer vi att ha lasten:

C = q/v → q (t) = cv = cv_m Sen ωt

Och med lasten beroende på tid kommer vi att ha strömmen, vilket är derivatet av det:

Yo_C(t) = cv_m Ω cos ωt

Men bröst och kosinus är relaterade genom: cos α = sin (α + π/2), därför:

Yo_C(t) = cv_m Ω sen (ωt + π/2) = i_C Sen (ωt + π/2)

Med i_C = CV_C Ω

Som man kan se är det en skillnad på 90º framsteg av strömmen med avseende på spänningen, som kommenterade i början.

Kan tjäna dig: Millikan Experiment: Procedure, Förklaring, betydelse

I beskrivningen av denna typ av kretsar, begreppet Fasor, som ser mycket ut som en vektor och gör det möjligt att representera i det komplexa planet varje växelmängd som ström, spänning eller impedans.

Följande figur visar, till höger, spänningen och nuvarande fasorerna i kondensatorn, som bildar en vinkel på 90º, vilket är fördröjningen mellan de två.

Till vänster finns respektive grafer, olika amplituder, men lika frekvens. Med tiden är strömmen fram till spänningen och när detta är maximalt är strömmen noll och när spänningen är noll är strömmen maximal men med den inverterade polariteten.

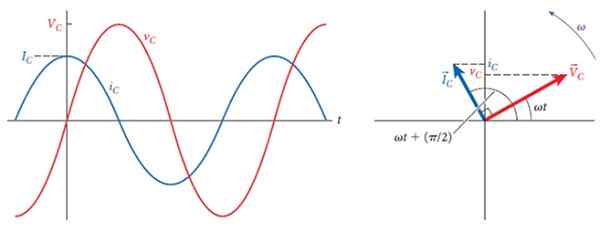Figur 3. 90º fördröjning mellan strömmen och spänningen genom en kondensator. Källa: Bauer, W.

Komplex kondensorimpedans

I en krets med motstånd, kondensatorer och induktanser är reaktans den imaginära delen av Z -impedansen, en komplex mängd som i växlande strömkretsar har en roll som liknar den för elektrisk motstånd för likström de för likström.

I själva verket definieras impedansen för en krets som orsaken mellan spänningen och strömmen:

Z = v / i

För en kondensator eller kondensator ges dess impedans av kvoten:

Z_C = v (t) / i (t) = v_C Sen ωt / i_C Sen (ωt + π/2)

Ett sätt att uttrycka spänning och ström som fasor är att indikera amplituden och fasvinkeln (polär form):

v (t) = v_C ∠ 0º

I (t) = i_C ∠ 90º

Därför:

Z_C = V_C ∠ 0º / i_C ∠ 90º = (v_C / Yo_C) ∠ 0º -90º =

= V_C / CV_C Ω ∠ -90º = (1/ ωC) ∠ -90º =

Z_C = (- j) x_C

Det vill säga, kondensorns impedans är dess kapacitiva reaktans multiplicerat med den negativa enhetens negativa.

Impedans av en serie RC -krets

Impedansen av en växlande strömkrets med motstånd, kondensatorer och induktorer kan också representeras binomiellt genom:

Det kan tjäna dig: första lagen om termodynamik: formler, ekvationer, exempel

Z = r + jx

I denna ekvation representerar r motståndet, som motsvarar den verkliga delen, j är den imaginära enheten och x är reaktansen, som kan vara kapacitiv eller induktiv eller kombination av båda, om dessa element finns samtidigt i kretsen.

Om kretsen innehåller ett motstånd och en seriekondensator är dess impedans:

Z = z_R + Z_C    

Som i motståndsspänning och ström är i fas, är resistiv impedans helt enkelt värdet på motstånd R.

När det gäller kapacitiv impedans har vi redan sett att z_C = -Jx_C , Därför är RC -kretsens impedans:

Z = r - jx_C = R - j (1/ ωc)

Till exempel i kretsen som visas nedan, vars källa är av formen:

100 V ⋅ SEN (120πt)

Observera att ω = 120π är impedansen:

Z = 83.0 - J [(1 / (120π ⋅ 6 x 10^-6)] ohm = 83.0 - 442.1 J ohm.

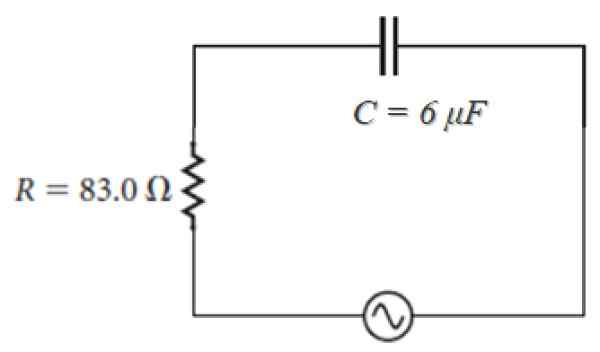Figur 4. RC Circuit Series med växlande nuvarande källa. Källa: f. Zapata.

Kapacitiva reaktansapplikationer

Pasa högfilter, lågpassfilter, brokretsar för att mäta kapacitanser och induktanser och kylkretsar är bland de huvudsakliga kretsapplikationerna som innehåller kapacitiva reaktanser, i kombination med induktanser och elektriska motstånd.

I ljudutrustning har vissa högtalare separata typer av typ BASHÖGTALARE (större) för låga frekvenser och Tweeter eller litet horn för höga frekvenser. På detta sätt förbättras ljudets prestanda och kvalitet.

De används kondensatorer som förhindrar ankomsten av låga frekvenser i tweeten, medan en induktor tillsätts i woofern för att undvika högfrekvenssignaler, eftersom induktans har en reaktans proportionell mot frekvensen: x x_L = 2πfl.

Referenser

1. Alexander, c. 2006. Elektriska kretsfundament. 3: e. Utgåva. MC Graw Hill.
2. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 2. MC Graw Hill.
3. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Volym 6. Elektromagnetism. Redigerad av Douglas Figueroa (USB).
4. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
5. Serway, R., Jewett, J. 2008. Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.