Rak och semi -rereed segment

En linje med linje och en halv -rätt är differentierade i det faktum att linjesegmentet är begränsat; det vill säga deras initiala punkt och deras slutpunkt är kända. Från semi -rätten är känd sin ursprungliga punkt, men inte dess slutpunkt, eftersom den sträcker sig till oändligheten.

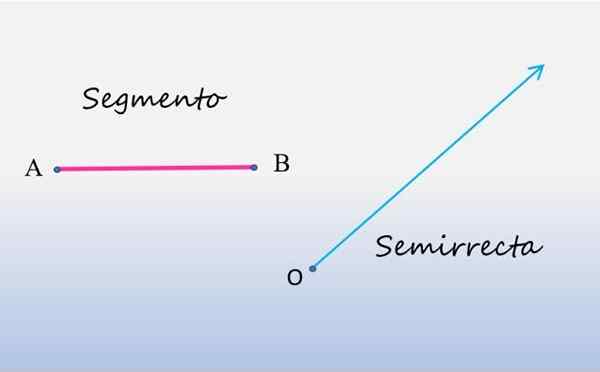
Följande figur visar, till vänster, ett linjesegment och till höger, en semi -rätt:

Segment och semi -rätt. Källa: f. Zapata.

Som man kan se är segmentet en linje med linje, som börjar vid punkt A och slutar vid punkt B, dessa punkter är ändarna på nämnda segment. Mätningen av segmentet motsvarar längden mellan dess ändar.

För sin del har semi -rätten sin utgångspunkt vid punkten O och sträcker sig till oändlighet, vilket motsvarar att det bara är begränsat i ena änden, vanligtvis kallad ursprung. Av denna anledning kallas de också gode Gud.

Segmenten betecknas genom bokstäverna som indikerar den ursprungliga punkten och slutet. Till exempel är segmentet av figuren segment AB, eller en stroke placeras på toppen, så här:

Å andra sidan kan en semi -återvinning också utses med två brev, en som anger punkten som motsvarar ursprunget och ytterligare ett ytterligare brev. Det kan också användas ett litet brev för att representera blixt eller semi -rekreation, och det finns också semi -rakt med sitt eget namn, vilket kommer att ses i exemplen senare.

Exempel på segment

Segmenten är mycket viktiga i geometri, nedan är några av de mest anmärkningsvärda:

Sidor av en polygon

Polygonerna är platta och stängda figurer, vars sidor är icke -konsekutiva linjesegment. Till exempel har en triangel tre sidor, en fyrkant har fyra sidor, en Pentagon har fem och så vidare.

Det kan tjäna dig: Tesseldos: karakteristiska, typer (vanliga, oregelbundna), exempel

Omkretsens diameter

Det definieras som det segmentet som innehåller två punkter i omkretsen och nödvändigtvis passerar genom mitten av samma.

En omkrets

När ett segment som förenar två punkter i omkretsen inte går igenom dess centrum, kallas det rep.

Triangelhöjd

Höjden på en triangel definieras som segmentet som går vinkelrätt från en av triangelns sidor till motsatt toppunkt. Om måttet på basen på en triangel, kallad B och höjden på samma, betecknad som H är känd, beräknas området A av samma genom den välkända formeln:

A = ½ b ∙ h

Semirret Exempel

Halvstrålning är också mycket viktiga element i geometri. Några välkända semi -rakt är:

De positiva semi -meddelandena

De tre riktningarna i rymden: hög, bred och djup, kan representeras av ett system med kartesiska axlar, bestående av tre ömsesidigt vinkelräta linjer med varandra, betecknade som axlar x, och och z, som skärs vid en punkt som heter ursprung.

Denna bestämmelse delar utrymme i åtta regioner kända som Oärter. I följande figur observeras de positiva halvdörrarna x, och och z, som bestämmer den första ocanten. På liknande sätt bestämmer den positiva halv -x y y regionen för planet som heter Första kvadrant.

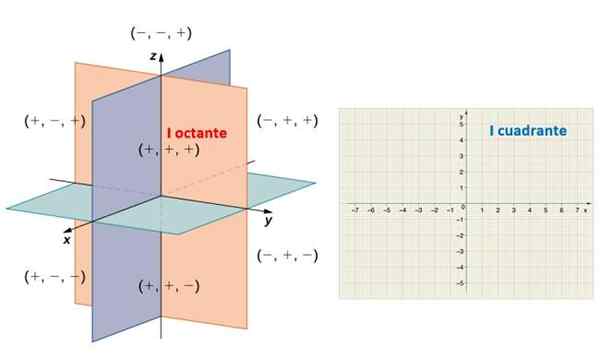Till vänster, de åtta oktoterna i rymden och till höger, det kartesiska planet uppdelat i fyra kvadranter. Källa: Math Librettexts.

Sidorna på en vinkel

En vinkel är bråkdelen av planet som avgränsas av två semi -vakt vars ursprung är vanligt. Denna punkt gemensamt är vertex av vinkeln, medan semi -strakt kallas respektive inledande sida och sista sida av vinkeln. Sådan bestämmelse visas i följande figur:

Det kan tjäna dig: vad är förhållandet mellan rombområdet och rektangeln?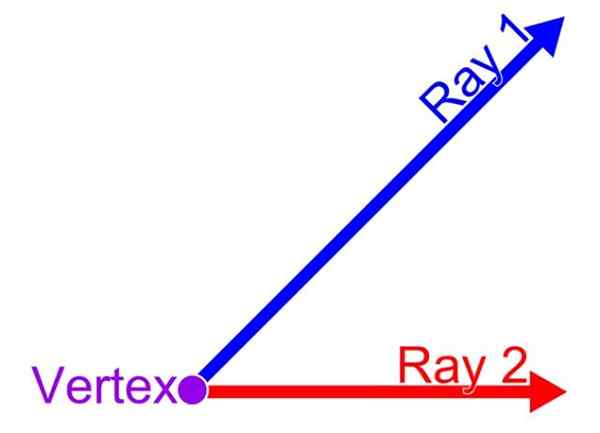 Element i en vinkel. Källa: Wikimedia Commons.