Axiella symmetriegenskaper, exempel och övningar

De Axiell symmetri Det inträffar när punkterna i en figur sammanfaller med punkterna i en annan figur med hjälp av en rak mediatrix som kallas symmetriaxel. Det kallas också radiell, roterande eller cylindrisk symmetri.

Det appliceras vanligtvis i geometriska figurer, men det kan lätt observeras, eftersom det finns djur som fjärilar, skorpioner, hyllor eller ordentligt människor som presenterar axiell symmetri.

På detta foto av horisonten i staden Toronto och dess reflektion i vattenaxiell symmetri visas. (Källa: Pixabay)

[TOC]

Hur man hittar den symmetriska axialen

För att hitta den symmetriska axiella p 'för en p -punkt med avseende på en linje (l) utförs följande geometriska operationer:

1.- Vinkelrätt mot linjen (L) spåras som passerar genom punkt P.

2.- Avlyssningen av de två linjerna bestämmer en punkt eller.

3.- Längden på PO -segmentet mäts, sedan kopieras denna längd på linjen (PO) från eller i riktning mot P A eller bestämmer punkten P '.

4.- Point P.

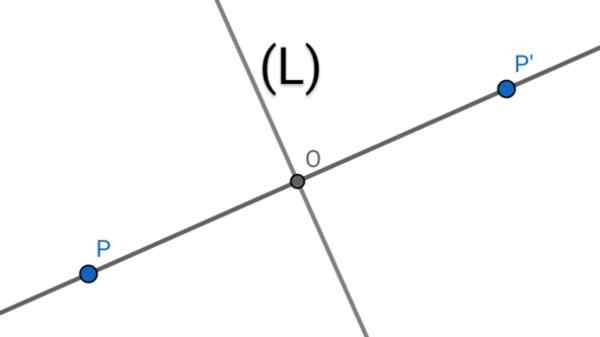Figur 1. Två punkter p och p 'är axiellt symmetriska för en axel (l) om nämnda axel är mediatrix för PP -segmentet'

Egenskaper hos axiell symmetri

- Axiell symmetri är isometrisk, det vill säga avståndet från en geometrisk figur och dess motsvarande symmetriska.

- Måttet på en vinkel och den för dess symmetriska är desamma.

- Den symmetriska axeln för en punkt på symmetriaxeln är själva punkten.

Det kan tjäna dig: Gauss-Seidel Method: Förklaring, applikationer, exempel

- Den symmetriska linjen för en linje parallell med symmetriaxeln är också en stall parallell med nämnda axel.

- En sekantslinje till symmetriaxeln är symmetrisk.

- Den symmetriska bilden av en linje är en annan linje som bildar en vinkel med symmetriaxeln för samma mått som den för den ursprungliga linjen.

- Den symmetriska bilden av en linje vinkelrätt mot symmetriens axel är en annan linje som överlappar den första.

- En linje och dess axiella symmetriska linje bildar en vinkel vars bisektor är symmetriens axel.

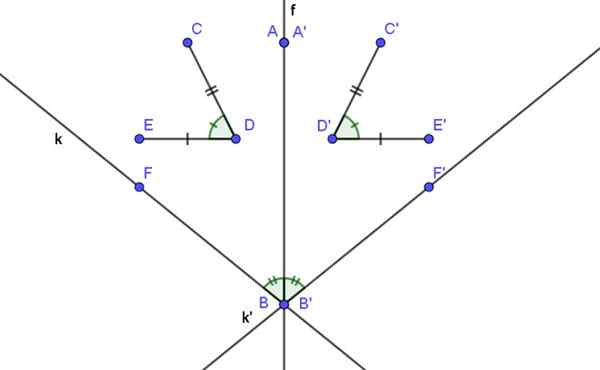figur 2. Axiell symmetri bevarar avstånd och vinklar.

Exempel på axiell symmetri

Naturen uppvisar rikliga exempel på axiell symmetri. Till exempel kan du se symmetrin från ansikten, insekter som fjärilar, reflektionen på ytor av lugna vatten och speglar eller bladen på växterna, bland många andra.

Figur 3. Denna fjäril uppvisar nästan perfekt axiell symmetri. (Källa: Pixabay) Figur 4. Den här flickans ansikte har axiell symmetri. (Källa: Pixabay)

Axiella symmetriövningar

Övning 1

Du har triangeln av vertikaler A, B och C vars kartesiska koordinater är respektive A = (2, 5), B = (1, 1) och C = (3.3). Hitta de kartesiska koordinaterna för den symmetriska triangeln med avseende på Y -axeln (ordinatens axel)).

Lösning: Om en punkt P har koordinater (x, y) är det symmetriskt med avseende på ordinatens axel (y-axeln) p '= (-x, y). Med andra ord.

Kan tjäna dig: oändlig uppsättning: egenskaper, exempel

I det här fallet kommer den symmetriska triangeln av toppar a ', b' och c 'att ha koordinater:

A '= (-2, 5); B '= (-1, 1) och C' = (-3, 3) Som kan kontrolleras i figur 6.

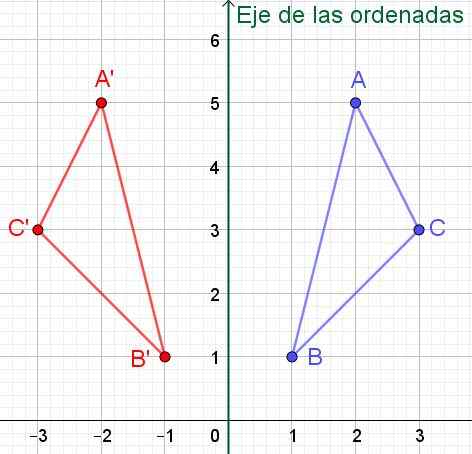Figur 6. Om en punkt har koordinater (x, y) är det symmetriskt med avseende på y-axeln (ordinatens axel) kommer att ha koordinater (-x, y).

Övning 2

Med hänvisning till ABC -triangeln och dess symmetriska a'b'c 'av övning 1, kontrollera att motsvarande sidor av den ursprungliga triangeln och dess symmetriska har samma längd.

Lösning: För att hitta avståndet eller längden på sidorna använder vi euklidisk avståndsformel:

d (a, b) = √ ((bx-ax)^2 + (by-ay)^2) = √ ((1-2)^2 + (1-5)^2) = √ (-1 )^2 + (-4)^2) = √ (17) = 4.123

Därefter beräknas längden på den symmetriska sidan motsvarande'b ':

D (a ', b') = √ ((bx'-ax ')^2 +(av'-y^2) = √ ((-1 +2)^2 +(1-5)^2) = √ ((1)^2 + (-4)^2) = √ (17) = 4,123

På detta sätt är det bevisat att axiell symmetri bevarar avståndet mellan två punkter. Förfarandet kan upprepas för de andra två sidorna av triangeln och dess symmetriska för att kontrollera invariansen i längden. Till exempel | AC | = | A'c '| = √5 = 2 236.

Övning 3

I förhållande till ABC -triangeln och dess symmetriska a'b'c 'av övning 1, kontrollera att motsvarande vinklar på den ursprungliga triangeln och deras symmetriska har samma vinkelmått.

Lösning: För att bestämma måtten på vinklarna bac och b'a'c 'den skalära produkten från vektorerna kommer att beräknas först Ab med Växelström och sedan den skalära produkten av A'b ' med A'c '.

Kom ihåg det:

A = (2, 5), B = (1, 1) och C = (3.3)

A '= (-2, 5); B '= (-1, 1) och C' = (-3, 3).

Du har:

Ab = y Växelström =

liknande

A'b ' = y Växelström =

Kan tjäna dig: Lamy Theorem

Sedan hittas följande skalprodukter:

Ab⋅ac = ⋅ = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7

Liknande

A'b'⋅a'c ' = ⋅ = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7

Måttet på BAC -vinkeln är:

∡bac = arccos ( Ab⋅ac / (|Ab |⋅ |Ac |)) = 

Arccos (7 / (4 123⋅2,236)) = 40,6º

På liknande sätt är måttet på vinkeln B'a'c ':

∡b'a'c '= arccos ( A'b'⋅a'c ' / (|A'b '|⋅ |A'c '|)) = 

Arccos (7 / (4 123⋅2,236)) = 40,6º

Avsluta att axiell symmetri bevarar mått på vinklar.

Övning 4

Vara en punkt P för koordinat (A, B). Hitta koordinaterna för dess symmetriska axiella p 'med avseende på linjen y = x.

Lösning: Vi kommer att ringa (a ', b') till koordinaterna för den symmetriska punkten p 'med avseende på linjen y = x. Segmentets mittpunkt m har koordinater ((a+a ')/2, (b+b')/2) och är också på linjen y = x, så följande jämlikhet uppfylls:

A + a '= b + b'

Å andra sidan har segmentet PP 'väntat -1 för att vara vinkelrätt mot linjen y = x av lutningen 1, så följande jämlikhet uppfylls:

B - B '= A' -A

Rensa de två jämställdheterna före 'och B' dras slutsatsen att:

a '= b och vad b' = a.

Det vill säga, med tanke på en punkt P (a, b), dess symmetriska axiala med avseende på linjen y = x är p '(b, a).

Referenser

1. Arce m., Blázquez S och andra. Planomvandlingar. Återhämtat sig från: Educutmxli.Filer.WordPress.com
2. CC -beräkning. Axiell symmetri. Återhämtad från: beräkning.Likström
3. Superprof. Axiell symmetri. Återhämtat sig från: superprof.är
4. Wikipedia. Axiell symmetri. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Symmetricirkulär. Hämtad från: i.Wikipedia.com