REVOLUTION FOLDA VOLUM, TYPER, LÖSNINGAR ÖVAR

han Revolution Solid Det är den tre -dimensionella figuren som genereras genom rotation av en plan yta runt den axiella axeln eller revolutionaxeln. Figur 1 visar en animation av ett fast revolution som genereras på detta sätt.

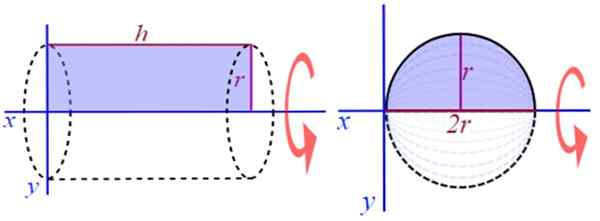
Ett annat mycket enkelt exempel att visualisera är att generera en rak cirkulär cylinder, rotera en rektangel av höjd eller lång H och radio R, runt den positiva X -axeln (figur 2). För att hitta sin volym finns det en välkänd formel:

V = basområde x höjd

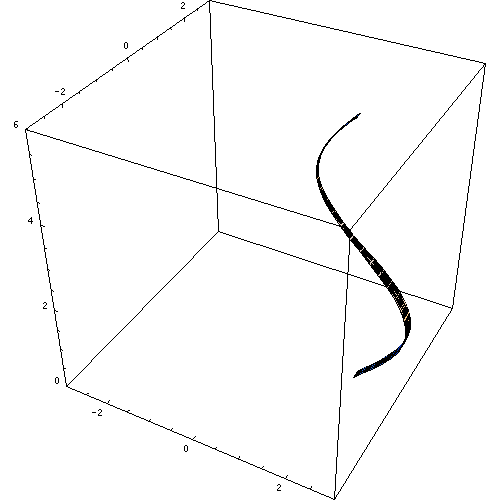Figur 1. Figuren som genererats genom rotationen av en SEN X -kurva. Källa: Wikimedia Commons. Macks/CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/2.5).

Andra revolutionella fasta ämnen är sfären, den raka cirkulära konen och olika figurer, enligt ytan placerad i rotation och naturligtvis den valda axeln.

figur 2. Generering av en rak cirkulär cylinder och en sfär. Källa: Wikimedia Commons.

Rotering av halvcirkeln runt en linje till exempel erhålls till diametern som ett fast ämne av ihålig revolution erhålls.

För cylindern, konen, sfären, både massiv och hål finns det formler för att hitta volymen, som beror på radien och höjden. Men när de genereras av andra ytor beräknas volymen genom definierade integraler.

[TOC]

Typer av revolutionella fasta ämnen

Revolutionfasta ämnen kan klassificeras enligt kurvan som genererar dem:

Sfär

Det räcker för att rotera en halvcirkel runt en axel som kommer att vara diametern på Radio R -sfären. Dess volym är:

V_sfär = (4/3) πr³

Fitta

För att få en H- och Radio R -kon, ytan som måste. Dess volym är:

V_Fitta = (1/3) πhr²

Cylinder

Roterande en rektangel runt en axiell axel som passerar genom en sidor, som kan vara den korta sidan eller den långa sidan, en rak cirkulär cylinder av radie R och höjd H erhålls, vars volym är:

Kan tjäna dig: rep (geometri): längd, sats och övningar

V_cylinder = πr²H

Toroid

Tjuren har formen av en munk. Det erhålls genom att rotera ett cirkulärt område runt en linje i planet som inte korsar cirkeln. Dess volym ges av:

V_Toroid = 2πa²R

Där A är radien för tvärsnittet och r är toroidens radie enligt schemat som presenteras i figuren:

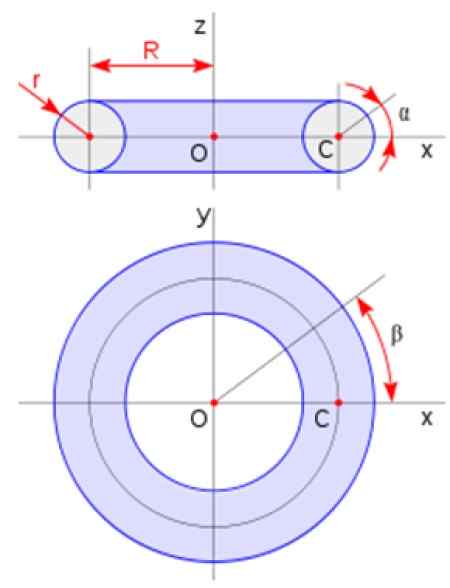Figur 3. Toroiddimensioner. Källa: Wikimedia Commons.

Metoder för att beräkna volymen på en revolution

Vid integrerad beräkning är dessa två metoder ofta:

-Skivor och brickor

-Skal

Skivmetod eller brickor

När skivan är ett fast revolution, kan tvärsnittet vara ett album, om det fasta är fast eller om det kan vara en slags bricka (ett album med ett hål i mitten), om det är ett fast hål.

Anta att en platt region roteras runt den horisontella axeln. Från den platta regionen tar vi en liten rektangel med Δx bredd, som roteras vinkelrätt runt axiella axeln.

Rektangelns höjd är mellan den yttersta kurvan R (x) och den mest interna r (x). De motsvarar den externa radien respektive intern radio.

När man gör denna rotation genereras en ΔV -volymbricka, ges av:

ΔV = full volym - hålvolym (om någon)

Kom ihåg att volymen på en rak cirkulär cylinder är π. radio² x höjd, vi har:

ΔV = π [r²(x) - r²(x)] Δx

Det fasta ämnet kan delas upp i en mängd små delar av volym ΔV. Om vi ​​lägger till dem alla kommer vi att ha hela volymen.

För att göra detta tenderar vi att 0 volymen ΔV, som också blir mycket liten och blir en DX -differential.

Det kan tjäna dig: ömsesidigt icke -exklusiva händelser: egenskaper och exempel

Således har vi en integral:

V = ∫_till^b π [r²(x) - r²(x)] dx

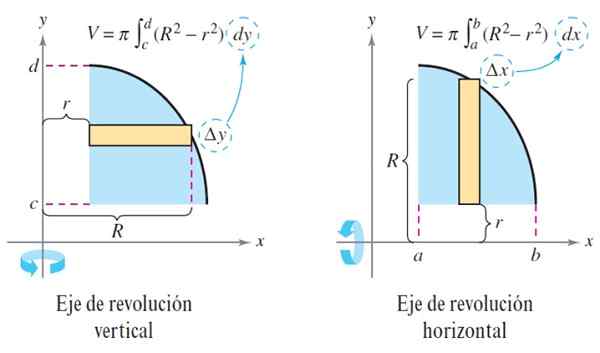Figur 3. Brickmetod. Källa: Larson. R. Beräkning.

I händelse av att det fasta är fast, är funktionen r (x) = 0, skivan på det fasta ämnet som genereras är en skiva och volymen återstår:

V = ∫_till^b πr²(x) dx

När revolutionsaxeln är vertikal tar de tidigare ekvationerna formen:

V = ∫_till^b π [r² (Y) - r² (y)] dy och v = ∫_till^b πr²(Y) Dy

Lager

Som namnet påpekar är denna metod att anta att det fasta ämnet består av differentiella tjocka lager. Skiktet är ett tunt rör som härstammar från en rektangel i parallellt med rotationsaxeln.

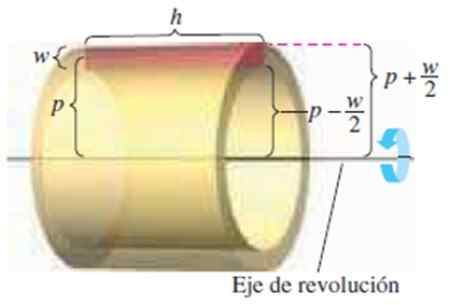Figur 4. Ett cylindriskt skikt av höjd 2, lång H och radie p. Källa: Larson, R. Beräkning.

Vi har följande dimensioner:

-Rektangelns höjd W

-Dess longitud h

-Avståndet från mitten av rektangeln till rotationsaxeln p

Att veta att volymen på skiktet är utomhusvolym - inre volym:

π (p + w/2)²H - π (p - w/2)²h

När man utvecklar anmärkningsvärda produkter och förenklande erhålls det:

Skiktvolym = 2π⋅p⋅w⋅h

Låt oss nu göra höjden W för rektangeln Δy, som ses i följande figur:

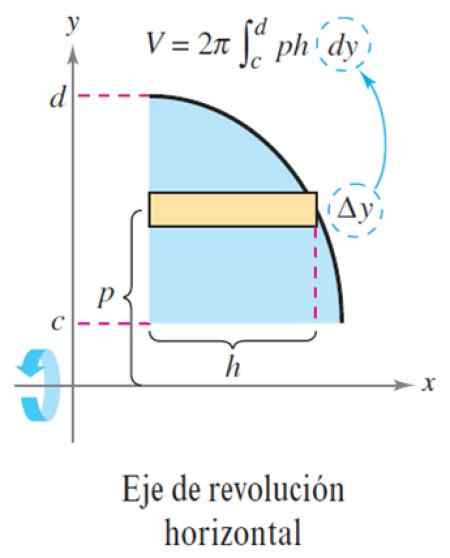Figur 5. Horisontell revolutionsaxellager -metod. Källa: Larson, R. Beräkning av en variabel.

Med detta är volymen ΔV:

ΔV = 2π p x h x Δy

Och att göra antalet lager n Var mycket stor, ΔY blir en differentiell dy, så att den totala volymen är integralen:

V = ∫_c^d 2π p (y) h (y) dy

Det beskrivna förfarandet tillämpas på liknande sätt när revolutionsaxeln är vertikal:

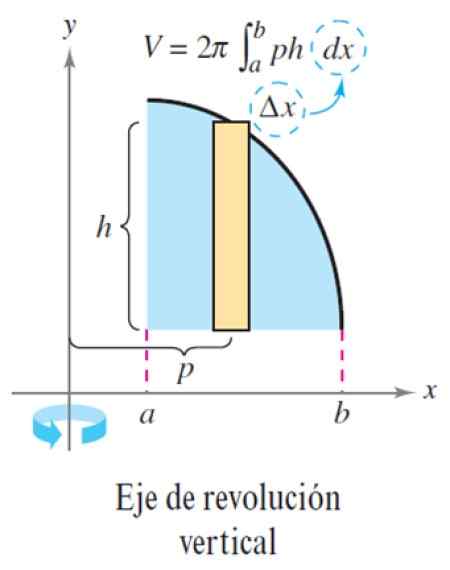Figur 6. Skiktmetod för vertikal revolutionsaxel. Källa: Larson, R. Beräkning av en variabel.

Träning löst

Hitta den volym som genereras genom rotationen av det platta området mellan kurvorna:

y = x²;  y = 0; x = 2

Runt axeln och.

Kan tjäna dig: negativ homotecia

Lösning

-Det första man ska göra är att grafera regionen som kommer att generera revolutionen fast och påpeka vändaxeln. Vi har det i följande graf:

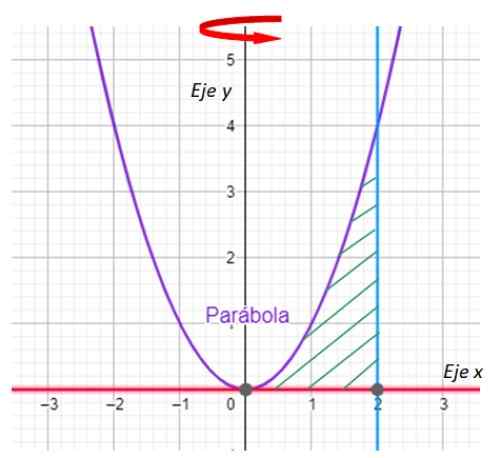Figur 7. Graf över kurvorna för övningen löst. Källa: f. Zapata med geogebra.

-Nu söks skärningspunkten mellan kurvan y = x² och linjen x = 2. För sin sida är linjen y = 0 ingen annan än x -axeln.

Det är lätt att varna att liknelsen och linjen korsar varandra vid punkten (2,4), vilket bekräftas genom att ersätta x = 2 på y = x².

-Sedan väljs en av metoderna för att beräkna volymen, till exempel skiktmetoden med vertikal revolutionsaxel:

V = ∫_till^b 2π p (x) h (x) dx

Steg 1: Rita rektangeln

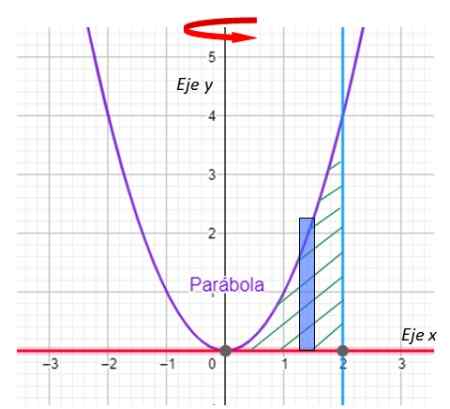Figur 8. Rektangel för det lösta exemplet. Källa: f. Zapata med geogebra.

Viktig: I skiktmetoden är rektangelns långa sida parallell med rotationsaxeln.

Steg 2: Bestäm p (x)

Skiktets lager är x

Steg 3: Bestäm h (x)

Rektangelns höjd bestäms av liknelse x².

Steg 4: Upprätta och lösa volymintegralen

Integrationsvariabeln är X, som varierar mellan 0 och 2, med detta har vi integrationsgränserna. Ersätta uttryck för p (x) och h (x)

 Vissa övningar kan lösas med båda metoderna. Kan läsaren lösa detta med tvättmoderna?

Referenser

1. Larson, r. 2010. Beräkning av en variabel. 9na. Utgåva. McGraw Hill.
2. Purcell, E. 2007. Beräkning med analytisk geometri. 9na. Utgåva. Pearson Education.
3. Wikipedia. Revolution. Hämtad från: i.Wikipedia.org.
4. Wikipedia. Toroid. Återhämtad från: är.Wikipedia.org.
5. Wolfram Mathworld. Revolution. Återhämtat sig från: Mathworld.Volfram.com.