De är de rektilinala segmenten som är möjliga i varje polygon

Diagonalen på ett fyrkant

De rätlinjiga segmenten som är möjliga i varje polygon är diagonaler. En diagonal är ett linjesegment som ritas genom att gå med två icke -angränsande vertikaler i en polygon. Med andra ord, de diagonala linjerna börjar vid ett toppunkt i figuren och hamnar i en annan som inte är nästa.

På bilden ovan visas diagonalen på en fyrkant i svart stroke, som som framgår, sammanfogar två motsatta hörn.

Diagonalerna på fyrkanten mäter samma, men i romb är deras två diagonaler olika, det finns en större, längre och en kortare, kortare kortare.

Hur man beräknar det diagonala antalet en polygon?

Att bestämma antalet diagonaler i en polygon kan vara enkelt när det gäller en kvadrat eller en romb, men när antalet sidor av en figur ökar blir det mer komplicerat att visualisera hur många diagonaler den har.

Det är därför en enkel formel som gör denna process mycket effektivare används i matematik:

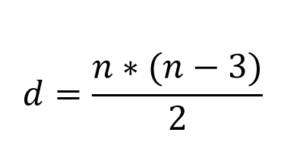
Det bör komma ihåg att N är lika med antalet sidor på polygonen, och N måste alltid vara större än 3. Därför att? (Fortsätt läsa, svaret är i slutet).

Exempel 1

Beräkna mängden diagonaler i en åttkant.

Octagon är en vanlig åtta -sidad polygon, detta innebär att alla dess inre sidor och vinklar är desamma.

Med den tidigare formeln räcker det för att ersätta N i åtta:

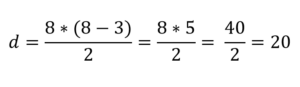
På detta sätt är det känt att antalet diagonaler som kan dras från vertikalerna hos en Octagon -polygon är 20.

Det kan tjäna dig: Vägt media: Hur det beräknas, exempel och övningar

Utan formeln är det förmodligen besvärligt att försöka räkna alla diagonaler, till och med ha en bra ritning. Och ju högre mängden sidor på figuren, desto mer komplicerad blir det.

Exempel 2

Beräkna längden på diagonalen på en rektangel med Pythagora -teoremet.

Pythagoras 'sats bekräftar att summan av rutorna i kategorierna av en rektangel triangel, kallad A och B, är lika med kvadratet för hypotenusen (sidan mittemot rätt vinkel), kallad C.

I algebraisk notation skulle det vara:

till² + b² = c²

Diagonalen i en rektangel bildar en rektangel triangel, som kan använda detta teorem, där B är basen och h är höjden.

Om basen är 12 cm och höjden är 7 cm, när du ersätter den är:

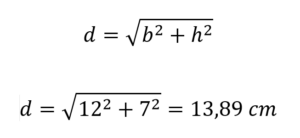
Därför är längden på diagonalen för nämnda rektangel 13,89 centimeter.

En polygon utan diagonaler

Är det möjligt att det finns en polygon som inte har diagonala linjer? Hur skulle det vara?

Denna gåta kan användas för att skjuta nyfikenhet hos barn och få dem att visualisera diagonalerna i en figur:

Triangeln är en tresidig polygon och som har tre inre vinklar. Men det har inga diagonaler

Ja, triangeln har inga diagonaler.

Förklaring

Triangeln är en tresidig polygon som har tre inre vinklar. Men trianglar är konvexa figurer som inte har diagonala linjer, som är de enklaste och mest fascinerande polygonerna i matematik.

Ser bra ut på formeln som gör att du kan beräkna diagonalerna i en polygon:

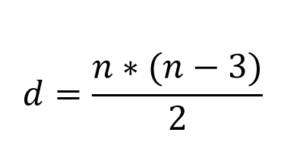
Det noteras omedelbart att genom att ersätta n = 3 erhålls det som ett resultat d = 0. Det vill säga trianglarna har inte diagonaler, det finns inget sätt att rita en. Men polygoner med n = 4 har till exempel alla två diagonaler.

Kan tjäna dig: Decagon: Regelbundet, oregelbundet, egenskaper, exempel