Kvadratiska framgångar Exempel, regel och övningar löst

De Kvadratiska efterföljningar, I matematiska termer består de av siffror som följer en viss aritmetisk regel. Det är intressant att veta denna regel för att fastställa någon av villkoren för en följd.

Ett sätt att uppnå detta är att bestämma skillnaden mellan två på varandra följande termer och se om det erhållna värdet upprepas alltid. När så sägs det att det är en ordinarie arv.

Numeriska successioner är ett sätt att organisera nummersekvenser. Källa: Pixabay.com

Men om det inte upprepas kan du försöka undersöka skillnaden mellan skillnader Och se om detta värde är konstant. Om så är fallet är det en Kvadratisk följd. 

[TOC]

Exempel på regelbundna successioner och kvadratiska efterföljningar

Följande exempel hjälper till att klargöra vad som har förklarats hittills:

Exempel på regelbunden succession

Vara successionen s = 4, 7, 10, 13, 16, ...

Denna arv, betecknad av S, är en oändlig numerisk uppsättning, i detta fall av hela siffror.

Det kan ses att det är en regelbunden succession, eftersom varje term erhålls genom att lägga till 3 till föregående term eller element:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Med andra ord: Denna succession är regelbunden eftersom skillnaden mellan följande termin och den föregående ger ett fast värde. I exemplet med detta värde är 3.

De regelbundna successionerna som erhålls genom att lägga till ett fast belopp till föregående termin, kallas också aritmetiska framsteg. Och till skillnaden - konstant - bland på varandra följande termer kallas det anledning Och det betecknas som r.

Exempel på icke -regelbunden och kvadratisk succession

Se nu följande följd:

S = 2, 6, 12, 20, 30, .. .

När de på varandra följande skillnaderna beräknas erhålls följande värden:

Kan tjäna dig: slumpmässiga val med eller utan ersättning

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Deras skillnader är inte konstant, så det kan sägas att det är en icke -regelbunden följd.

Men om vi överväger uppsättningen av skillnader finns det en annan följd, som kommer att betecknas som S_Diff:

S_Diff = 4, 6, 8, 10, .. .

Denna nya succession är en ordinarie arv, Eftersom varje term erhålls genom att lägga till det fasta värdet r = 2 till föregående. Det är därför vi kan bekräfta att S är Kvadratisk följd.

Allmän regel för att bygga en kvadratisk succession

Det finns en allmän formel för att bygga en kvadratisk följd:

T_n = A ∙ n² + B ∙ n +c

I denna formel, t_n Det är termen för n för successionen. A, B och C är fasta värden, medan N varierar en efter en, det vill säga 1, 2, 3, 4, ..

I följd av föregående exempel a = 1, b = 1 och c = 0. Därifrån följer det att formeln som genererar alla termer är: t_n = n² + n

Det vill säga:

T₁ = 1² + 1 = 2

T₂ = 2² + 2 = 6

T₃ = 3² + 3 = 12

T₅ = 5² + 5 = 30

T_n = n² + n

Skillnaden mellan två på varandra följande villkor för en kvadratisk följd

T_N+1 - T_n = [A ∙ (N+1)² + B ∙ (n + 1) + c] - [a ∙ n² + B ∙ n +c]

Att utveckla uttrycket genom anmärkningsvärd produkt kvarstår:

T_N+1 - T_n = A ∙ n² + A ∙ 2 ∙ n + a + b ∙ n + b + c - a ∙ n² - B ∙ n - c

Genom att förenkla det får du:

T_N+1 - T_n = 2 ∙ a ∙ n + a + b

Detta är formeln som ger följd av skillnaderna s_Diff som kan skrivas så här:

Diff_n = A ∙ (2n+1)+b

Där tydligt följande termin är 2 ∙ ibland det föregående. Det vill säga orsaken till följd av skillnaderna_Diff Es: r = 2 ∙ a.

Löst övningar av kvadratiska efterföljningar

Övning 1

Vara successionen s = 1, 3, 7, 13, 21, .... Bestäm ja:

i) det är regelbundet eller inte

ii) är kvadratisk eller inte

iii) var kvadratisk, följd av skillnader och deras anledning

Det kan tjäna dig: Begränsa egenskaper (med exempel)

Svar

i) Låt oss beräkna skillnaden följande termin och den föregående:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Vi kan bekräfta att succession inte är regelbunden, eftersom skillnaden mellan på varandra följande termer inte är konstant.

ii) Successionen av skillnaderna är regelbunden, eftersom skillnaden mellan dess termer är det ständiga värdet 2. Därför är den ursprungliga successionen kvadratisk.

iii) Vi har redan fastställt att S är kvadratiskt, följd av skillnaderna är:

S_Diff = 2, 4, 6, 8, ... och dess anledning är r = 2.

Övning 2

Vara successionen s = 1, 3, 7, 13, 21, ... i föregående exempel, där det verifierades att det är kvadratiskt. Bestämma:

i) formeln som bestämmer den allmänna termen t_{n .}

ii) Verifiera den tredje och femte terminen.

iii) värdet på den tionde terminen.

Svar

i) den allmänna formeln för T_n är en ∙ n² + B ∙ n +c. Då är det känt värdena på A, B och C.

Arvén av skillnader är rätt 2. Förutom alla kvadratiska följder anledningen till att r är 2 ∙ a som demonstreras i föregående avsnitt.

R = 2 ∙ a = 2 vilket leder till att vi drar slutsatsen att a = 1.

Den första terminen i följd av skillnader s_Diff Det är 2 och måste följa ∙ (2n+1)+B, med n = 1 och a = 1, det vill säga:

2 = 1 ∙ (2 ∙ 1+1)+B

Clearing B erhålls: B = -1

Sedan den första termen av S (n = 1) Vale 1, det vill säga: 1 = A ∙ 1² + B ∙ 1 + c. Som vi redan vet att A = 1 och B = -1, ersätter oss, är vi kvar:

1 = 1 ∙ 1² + (-1) ∙ 1 +c

Clearing C erhålls sitt värde: C = 1.

Sammanfattningsvis:

A = 1, b = -1 och c = 1

Då är termen bara_n = n² - N + 1

ii) den tredje termen t₃ = 3² - 3 + 1 = 7 och verifieras. Den femte t₅ = 5² - 5 + 1 = 21 som också verifieras.

iii) den tionde termen kommer att vara t₁₀ = 10² - 10 + 1 = 91.

Övning 3

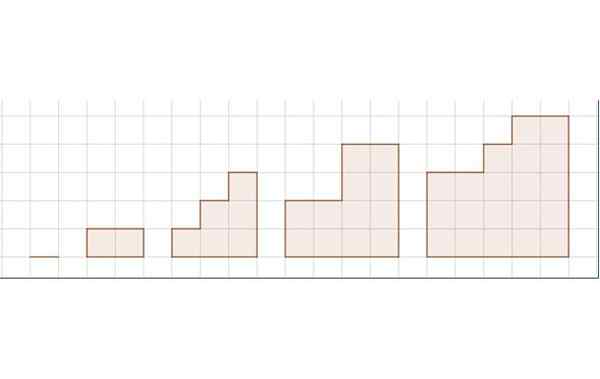Sekvens av områden för övning 3. Källa: Självgjord.

Figuren visar en sekvens av fem figurer. Retikulärt representerar längden enhet.

Kan tjäna dig: Skillnad mellan en gemensam fraktion och ett decimalnummer

i) Bestäm successionen för figurområdet.

i) visa att det är en kvadratisk följd.

iii) Hitta området i figur nr 10 (visas inte).

Svar

i) successionen som motsvarar området för figurens sekvens är:

S = 0, 2, 6, 12, 20, ...

ii) Den succession som motsvarar de på varandra följande skillnaderna i villkoren för S är:

S_Diff = 2, 4, 6, 8, ...

Eftersom skillnaderna mellan på varandra följande termer inte är konstant, så är inte en regelbunden succession. Den måste veta om det är kvadratiskt, för vilket vi återigen gör sekvensen för skillnaderna, erhåller:

2, 2, 2, .. .

Eftersom alla termer i sekvensen upprepas bekräftas att S är en kvadratisk följd.

iii) succession s_Diff är regelbunden och dess anledning är R 2. Med hjälp av den tidigare demonstrerade ekvationen R = 2 ∙ A, kvarstår:

2 = 2 ∙ a, vilket innebär att a = 1.

Den andra terminen i följd av skillnader s_Diff Det är 4 och N-EME för S_Diff är

A ∙ (2n+1)+b.

Den andra terminen har n = 2. Det fastställdes också att a = 1, så att använda den tidigare ekvationen och ersätta den är:

4 = 1 ∙ (2 ∙ 2+1)+B

Clearing B erhålls: B = -1.

Det är känt att den andra termen av S är värd 2, och att formeln för den allmänna termen måste uppfylla med n = 2:

T_n = A ∙ n² + B ∙ N +C; n = 2; A = 1; B = -1; T₂ = 2

Det vill säga

2 = 1 ∙ 2² - 1 ∙ 2 + c

Det dras slutsatsen att C = 0, det vill säga att formeln som ger den allmänna termen för successionen är:

T_n = 1 ∙ n² - 1 ∙ n +0 = n² - n

Nu verifieras den femte terminen:

T₅ = 5² - 5 = 20

iii) Figur 10, som inte har ritats här, kommer att ha området som motsvarar den tionde terminen för S -arv:

T₁₀ = 10² - 10 = 90

Referenser

1. https: // www.Geogebra.org