Bernoulli -teorem

Vi förklarar vad som är Bernoullis teorem, ekvationer, applikationer och löser en övning

Vad är Bernoullis sats?

han Bernoulli -teorem Han bekräftar att i en idealisk vätska som cirkulerar i en ledning är den mekaniska energin per volymenhet av vätskan konstant i alla rörsektionerna, oavsett att de har olika tvärsnitt av area och höjd.

Nu är en idealisk vätska en som inte kan komprimeras, så dess densitet är fixerad, oavsett tryckvärde.

Dessutom har en idealisk vätska nollviskositet, det vill säga det finns ingen friktion mellan vätskeskikten och varken mellan vätskan och kanalens väggar.

Förhållandena för inkomprimerbarhet och nollviskositet är viktiga för att tillämpa Bernoullis teorem. Det är också nödvändigt att flödet är stillastående, det vill säga flödet varierar inte med tiden.

Å andra sidan måste flödet vara laminärt, så det kan inte finnas några virvlar eller turbulens under kanalens passage.

Bernoulli -ekvation

Bernoulli -ekvationen har tre termer, arbetet som utförs av press P, kinetisk energi och gravitationspotentialenergi för varje volymdensitetsvätskenhet ρ ρ ρ

Bernoullis ekvation är:

Å andra sidan fastställer kontinuitetsekvationen att flödet i en idealisk vätska är konstant i alla delar av flödesröret. Det vill säga vätskevolymen i samma tidsenhet är densamma i alla delar av röret.

Om flödet är Q, då:

Q = konstant

Med:

Q = a · v

Där A är rörets tvärsnittsområde och v är vätskans hastighet.

Kan tjäna dig: konstgjorda satelliter

Det noteras att vätskan i de smalaste sektionerna i röret måste cirkulera snabbare, eftersom den förblir konstant även om den varierar. Därför är kinetisk energi per enhetsvolym större.

Eftersom Bernoullis sats konstaterar att mekanisk energi är konstant i alla sektioner, i de smalare sektionerna av större kinetisk energi minskar potentiell energi. 

Den potentiella energin består av gravitationsenergi per enhetsvolym plus arbetet som utförs av trycket i en enhetsvolym, därför genom att minska den potentiella energin minskar också trycket.

Sammanfattningsvis resulterar den kombinerade effekten av principen om kontinuitet och Bernoulli -teoremet i de smala sektionerna av flödesröret, där vätskehastigheten är större, trycket sjunker med avseende på de bredare sektionerna.

Termer i Bernoulli -ekvationen

1) Arbetet utfört av trycket per enhetsvolym 

I ett avsnitt av tvärsnitt av området till, Vätskan rör sig en mängd s, På grund av trycket p som producerar en kraft f = p⋅ a.

Det arbete som utförs med våld är:

F⋅ s = p⋅ a⋅ s

Eftersom A CarS -produkten representerar den fördrivna volymen, matchar det arbetet som gjorts per enhetsvolym numeriskt med värdet på P i det avsnitt som beaktas.

2) Kinetisk energi i en enhetsvolym

Eftersom vätskan är inkomprimerbar har dess densitet ett fast värde som kallas ρ.

När vätskan cirkulerar genom ett avsnitt av tvärsnitt A, flyttar en mängd S i en tid t, är flödeshastigheten:

Det kan tjäna dig: andra lagen om termodynamik: formler, ekvationer, exempel

v = s/t

Och den kinetiska energin i nämnda vätskeparti beräknas av:

K = ½ ρ (a⋅s) v²

Men om den fördrivna volymen (A⋅S) är enhet, kommer termen för kinetisk energi att ges av ½ ρ v².

3) Gravitationspotential energi för en enhetsvolym i en höjd h 

För en degvätskeparti m och höjd h När det gäller en viss referensnivå ges gravitationsenergi av:

U = m⋅ g⋅ h

Om degen m Det motsvarar en enhetlig vätskeparti, sedan matchar den täthetens massa tätheten ρ, Så den potentiella energin kommer att vara ρ⋅ g⋅ h.

Bernoulli Theorem -applikationer

Aerodynamisk stöd

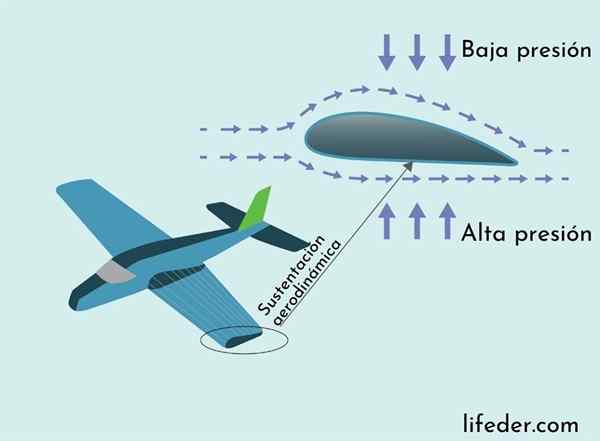Aerodynamiskt stöd förklaras av Bernoullis teorem

Kraften som förhindrar ett flygplan från flyg till kollaps är den aerodynamiska stödkraften. Netstödstyrkan riktas vertikalt upp och verkar längs planvingen. Dess ursprung förklaras genom Bernoullis teorem.

Vingens vinge har ett tvärsnitt med en längre kurva överst och kortare längst ner. Detta gör luftvägen nära vingens yta överst, så luften flyter snabbare över vingen än botten. 

Som en följd av Bernoullis sats är lufttrycket i den övre delen av den cirkulerande vingen mindre än längst ner, vilket resulterar i den kraft som utövas av tryckskillnaden riktas uppåt, vilket stödjer vikten på planet, enligt den kan vara sett i följande bild.

Det kan tjäna dig: fysik under grekerna (Antige Grekland)

Lansering av bollar och bollar med kurveffekt

I vissa sporter som fotboll, baseball och cricke vet erfarna spelare hur. Är det som kallas Effektlansering.

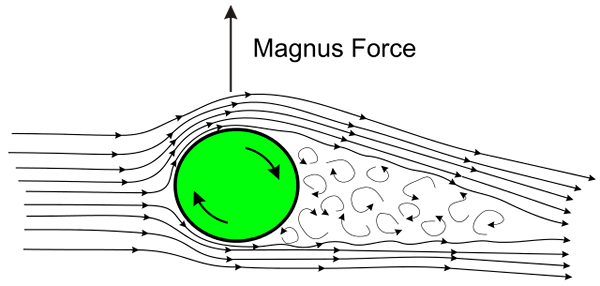Magnuseffektillustration. Källa: Wikimedia Commons

Effekten inträffar när bollen eller bollen svänger snabbt medan du rör sig genom luften. Rotationen orsakar luften till bollens yta dras av den i två motsatta riktningar, en till förmån för översättningsriktningen och på andra sidan mot förskjutningsriktningen.

Som ett resultat av luftdraget produceras ett lågt tryckområde på ett ansikte av bollen och på motsatt ansikte ett högt tryck, vilket producerar en nettokraft som leder bollens naturliga bana.

Förklaringen av detta fenomen känt som Magnuseffekt Det ligger exakt i Bernoullis sats: där vätskan cirkulerar snabbt är trycket lågt, och på sidan där trycket cirkulerar långsamt.

Träning löst

Ett horisontellt rör har ett area -avsnitt a₁ = 40 kvadratcentimeter och en annan del av området avsnitt a₂ Fyra gånger lägre. Om vattenflödet är 6 l/s, bestäm tryckskillnaden och höjdskillnaden i vertikala rör.

Lösning 

Börjar från flödesekvationen, vars värde är q = 6 l/s:

Q = a · v

Du måste då hastigheten i det breda avsnittet är 1,5 m/s och i den smala sträckan 6 m/s.

Sedan, tillämpning och matchning av Bernoulli -ekvationen på den breda och smala sträckan, erhålls en tryckskillnad på 1700 PA, vilket motsvarar en höjdskillnad i de vertikala rören på 1,72 meter.