Euklidteorem

Vad är Euclids teorem?

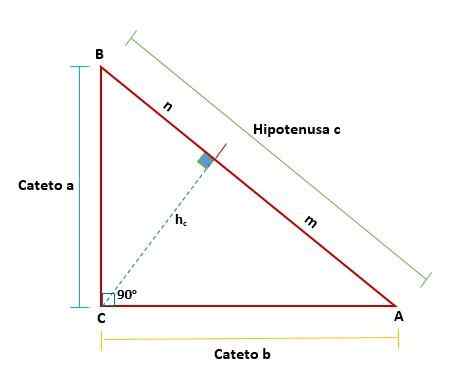
han Euklidteorem Den visar egenskaperna hos en höger triangel genom att rita en linje som delar upp den i två nya rektanglar som liknar varandra och i sin tur liknar den ursprungliga triangeln; Så det finns en proportionalitetsförhållande.

Euclides var en av de största matematiker och geometrar i ålderdomen som gjorde flera demonstrationer av viktiga teorier. En av de viktigaste är den som bär hans namn, som har haft en bred applikation.

Detta har varit så eftersom de geometriska förhållandena som finns i rektangelstriangeln, där detta är relaterat till deras prognoser i hypotenusen genom genom att sats i hypotenusen i hypotenusen.

Formler och demonstration

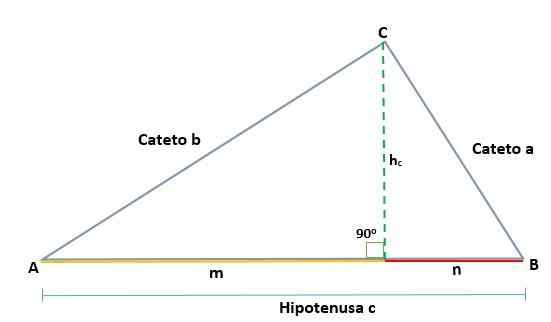
Euclid -teorem föreslår att i varje höger triangel, när en linje ritas - som representerar i höjden som motsvarar toppen av höger vinkel med avseende på hypotenusen - bildas två rektanglar från de ursprungliga trianglarna från originalet.

Dessa trianglar kommer att likna varandra och kommer också att likna den ursprungliga triangeln, vilket innebär att deras liknande sidor är proportionella mot varandra:

Vinklarna på de tre trianglarna är kongruenta; Det vill säga när den roteras vid 180 grader på sitt topp, sammanfaller en vinkel på den andra. Detta innebär att alla kommer att vara lika.

På detta sätt kan du också verifiera den likhet som finns mellan de tre trianglarna, för jämlikheten mellan dess vinklar. Eftersom likheten mellan trianglar, etablerar Euclid proportionerna av dessa från två teorem:

• Höjderem.
• Catetos -teoremet.

Detta sats har en bred tillämpning. I forntida tider användes det för att beräkna höjder eller avstånd, vilket representerar ett stort framsteg för trigonometri.

Kan tjäna dig: Beräkning av tillvägagångssätt med skillnader

Det tillämpas för närvarande inom olika områden som är baserade på matematik, såsom teknik, fysik, kemi och astronomi, bland många andra områden.

Höjderem

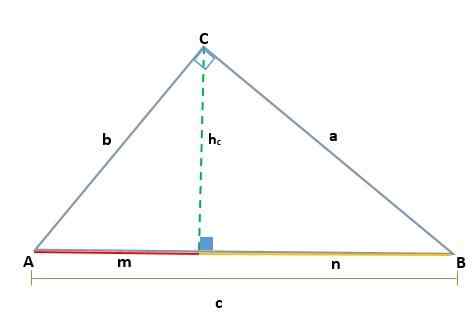
Detta sats konstaterar att i alla rektangelstriangel är höjden som dras från rätt vinkel med avseende på hypotenusen det geometriska proportionella genomsnittet (höjden av höjden) mellan prognoserna för kotetos som bestämmer på hypotenusen.

Det vill säga att höjden är lika med multiplikationen av de projicerade benen som bildar hypotenusen:

h_c² = m _* n

Demonstration

Med tanke på en ABC -triangel, som är rektangel i Vertex C, genereras två liknande rektanglar, ADC och BCD; Därför är deras motsvarande sidor proportionella:

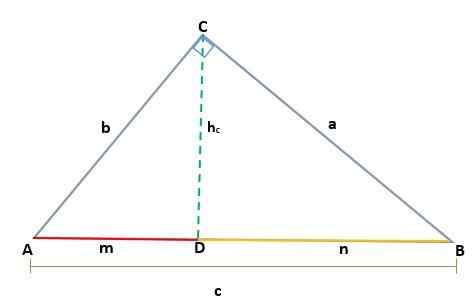
På ett sådant sätt att höjden h_c Det motsvarar CD -segmentet, motsvarar hypotenus AB = C, så du måste:

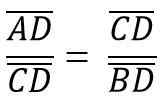
I sin tur motsvarar detta:

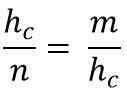
Rensa hypotenus (h_c), För att multiplicera de två jämställdhetsmedlemmarna måste du:

h_{C *} h_{C =} m _* n

h_c² = m _* n

Således ges värdet på hypotenusen av:

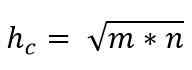
Catetos -teoremet

Detta sats konstaterar att måttet på varje kateto kommer att vara det geometriska proportionella genomsnittet i varje höger triangel

b² = c _* m

till² = c_* n

Demonstration

Med tanke på en ABC -triangel, som är rektangel i toppunkt C, så att dess hypotenusa är C, när du ritar höjden (h) prognoserna för kategorierna A och B bestäms, som är segmenten M och N Hypotenusen.

Således genererar höjden som dras på rektangel -triangeln ABC två liknande rektanglar, ADC och BCD, så att motsvarande sidor är proportionella, så här:

Kan tjäna dig: Hyperbolic Paraboloid: Definition, Egenskaper och exempel

Db = n, som är projiceringen av CB Cateto på hypotenusen.

Ad = m, som är projiceringen av ac cateto på hypotenusen.

Sedan bestäms hypotenus C av summan av benen på dess prognoser:

C = m + n

På grund av likheten mellan ADC och BCD -trianglar måste du:

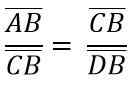
Ovanstående är detsamma som:

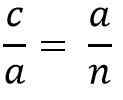
Rensa "A" Cateto för att multiplicera de två medlemmarna i jämlikhet, du måste:

till _* a = c _* n

till² = c _* n

Således ges värdet på Cateto "A" av:

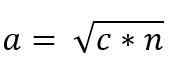
På samma sätt, på grund av likheten mellan ACB- och ADC -trianglar, måste du:

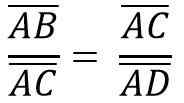
Ovanstående är lika med:

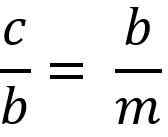
Rensa "B" Cateto för att multiplicera de två medlemmarna i jämlikhet, du måste:

b _* b = c _* m

b² = c _* m

Således ges värdet på Cateto "B" av:

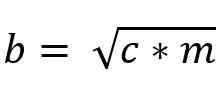
Förhållandet mellan euklidteorem

Satser med hänvisning till höjden och kategorierna är relaterade till varandra eftersom måtten på båda görs med avseende på hypotenusen av rektangelns triangel.

Genom förhållandet mellan Euclid -teorem kan värdet på höjden också hittas; Det är möjligt genom att rensa värdena på M och N i kategoristeoremet och ersätts i höjdteoremet. På detta sätt är det uppfyllt att höjden är lika med multiplikationen av benen, dividerat med hypotenusen:

b² = c _* m

m = b² ÷ c

till² = c _* n

n = a² ÷ c

I höjden byts teorem m och n:

h_c² = m _* n

h_c² = (B² ÷ c) _* (till² ÷ c)

h_c = (B² _* till²) ÷ c

Löst övningar

Exempel 1

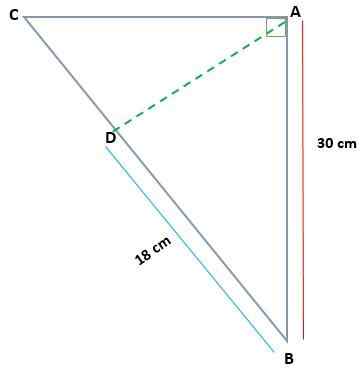
Med tanke på ABC -triangeln, rektangel i A, bestäm måtten på AC och AD, om AB = 30 cm och BD = 18 cm

Lösning

I det här fallet finns det måtten på ett av de projicerade benen (BD) och en av den ursprungliga triangelns striangel (AB). På så sätt kan du tillämpa kategoristeoremet för att hitta värdet på BC Cateto.

Kan tjäna dig: korrespondensregel för en funktion

Ab² = BD _* före Kristus

(30)² = 18 _* före Kristus

900 = 18 _* före Kristus

BC = 900 LL 18

BC = 50 cm

Värdet på CD -kateto kan hittas med att veta att BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Nu är det möjligt att bestämma värdet på AC Cateto, tillämpa igen kategorinsteoremet:

Växelström² = CD _* BD

Växelström² = 32 _* femtio

Växelström² = 160

AC = √1600 = 40 cm

För att bestämma höjdvärdet (AD) gäller höjdteoremet, eftersom värdena för de beräknade kategorierna CD och BD är kända:

Annons² = 32 _* 18

Annons² = 576

AD = √576

AD = 24 cm

Exempel 2

Bestäm värdet på höjden (h) på en MNL -triangel, rektangel i n, och känner till segmentens mått:

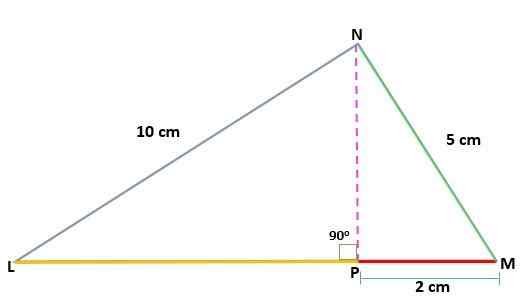
NL = 10 cm

Mn = 5 cm

PM = 2 cm

Lösning

Du har måtten på ett av de projicerade benen på hypotenusen (PM), liksom måtten på de ursprungliga triangelkategorierna. På så sätt kan du tillämpa kategoristeoremet för att hitta värdet på den andra projicerade Cateto (LN):

Nl² = Pm _* Lm

(10)² = 5 _* Lm

100 = 5 _* Lm

PL = 100 LL 5 = 20

Eftersom värdet på kategorierna och hypotenusen redan är känd, genom förhållandet mellan höjden teorem och kategorierna kan bestämmas värdet på höjden:

Nl = 10

Mn = 5

Lm = 20

H = (B² _* till²) ÷ c.

H = (10² _* 5²)  LL (tjugo)

H = (100 _* 25) LL (tjugo)

H = 2500 LL tjugo

H = 125 cm.