Trapecio Isosceles Egenskaper, relationer och formler, exempel

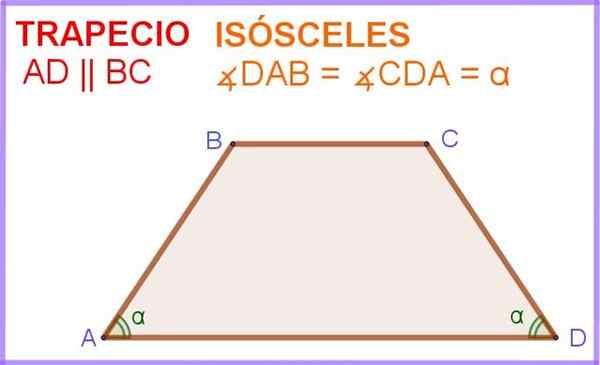
En trapets likbent Det är en fyrkantig där två av sidorna är parallella med varandra och även de två vinklarna intill en av dessa parallella sidor har samma mått.

I figur 1 har du ABCD -fyrkant, där AD- och BC -sidorna är parallella. Dessutom har vinklarna ∠DAB och ∠ADC intill den parallella sidan AD samma mått a. 

Figur 1. Trapeziumsosceler. Källa: f. Zapata.

Således är denna fyrkantiga eller fyra sidosidiga polygon i själva verket en isosceles trapezoid.

I en trapes kallas de parallella sidorna baser och icke-paralleller kallas lateral. En annan viktig funktion är höjd, vilket är avståndet som skiljer de parallella sidorna.

Förutom isosceles trapezoid finns det andra typer av trapes:

-TRapecio escaleno, som har alla sina olika vinklar och sidor.

-TRektangel rapecio, där en sida har raka angränsande vinklar.

Trapezoidal form är ofta inom olika områden inom design, arkitektur, elektronik, beräkning och många fler, vilket kommer att ses senare. Därför vikten av att bli bekant med sina egenskaper.

[TOC]

Egenskaper

Exklusiva likhet med trapesoid

Om en trapeze är iSosceles uppfyller följande karakteristiska egenskaper:

1.- Sidorna har samma mått.

2.- Vinklarna intill baserna är desamma.

3.- Motsatta vinklar är kompletterande.

4.- Diagonalerna har samma längd, samma är de två segmenten som förenar motsatta vertikaler.

5.- Vinkeln som bildas mellan baserna och diagonalerna är alla samma mått.

6.- Det har omskriven omkrets.

Ömsesidigt, om en trapes möter någon av de tidigare egenskaperna, är det en isosceles trapezoid.

Om en av vinklarna är rak (90º) i en trapezoid -isosceles, kommer också alla andra vinklar att bilda en rektangel. Det vill säga en rektangel är ett särskilt fall av isosceles trapezoid.

figur 2. Corn Palomites behållare och skolbord är formade som isosceles. Källa: PXFuel (till vänster)/McDowell Craig genom Flickr. (höger)

För alla trapesoid

Följande uppsättning egenskaper är giltiga för alla trapes:

7.- De median av trapes, det är det segment som ansluter sig till mittpunkterna på dess icke -parallella sidor, är parallell med någon av baserna.

8.- Medianens längd är lika med semi -Semum (summan dividerat med 2) av dess baser.

9.- Medianen för en trapezoid skär sina diagonaler vid mittpunkten.

10.- Diagonalerna i en trapes korsar vid en punkt som delar upp dem i två sektioner proportionella mot kvoten på baserna.

elva.- Summan av rutorna i diagonalerna i en trapes är lika med summan av rutorna på sidorna plus den dubbla produkten i dess baser.

Det kan tjäna dig: hur många tusendelar passar de i en tiondel?

12.- Segmentet som ansluter sig till mid -Diagonal -punkterna har längd lika med basreferensen för baserna.

13.- Vinklarna intill sidorna är kompletterande.

14.- En trapes har en registrerad omkrets om och bara om summan av dess baser är lika med summan av dess sidor.

femton.- Om en trapes har en registrerad omkrets, är vinklarna med toppunkt i mitten av nämnda omkrets och sidor som passerar genom ändarna på samma sida, raka vinklar.

Relationer och formler

Följande uppsättning relationer och formler hänvisas till figur 3, där förutom isosceles trapezoid andra viktiga segment som redan nämnts, såsom diagonaler, höjd och medium.

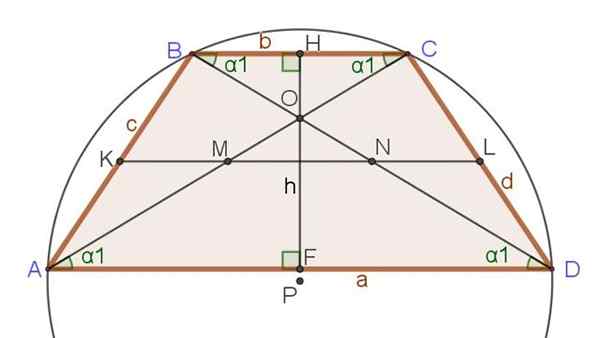Figur 3. Median, diagonaler, höjd och omkrets omskriven i en isosceles trapezoid. Källa: f. Zapata.

Exklusiva relationer mellan Isosceles Trapecio

1.- AB = DC = C = D

2.- ∡DAB = ∡CDA och ∡ABC = ∡BCD

3.- ∡DAB + ∡BCD = 180º och ∡CDA + ∡ABC = 180º

4.- BD = AC

5.- ∡cad = ∡bda = ∡cbd = ∡bca = α₁

6.- A, B, C och D tillhör den omskrivna omkretsen.

Relationer för alla trapesoider

7. Om AK = KB och DL = LC ⇒ KL || AD och KL || före Kristus

8.- Kl = (ad + bc)/2

9.- Am = mc = ac/2 och dn = nb = db/2

10.- AO/OC = AD/BC Y DO/OB = AD/BC

elva.- Växelström² + DB² = AB² + Likström² + 2⋅AD⋅BC

12.- Mn = (ad - bc)/2

13.- ∡DAB + ∡ABC = 180º och ∡CDA + ∡BCD = 180º

14.- Om AD + BC = AB + DC ⇒ ∃ R Vilken Equidista av AD, BC, AB och DC

femton.- Om ∃ r vilken equidista av AD, BC, AB och DC, då:

∡bra = ∡drc = 90º

Isosceles trapezoidförhållanden med registrerad omkrets

Om summan av baserna i en isosceles trapezoid är lika med den dubbla på en sida, så finns det den registrerade omkretsen.

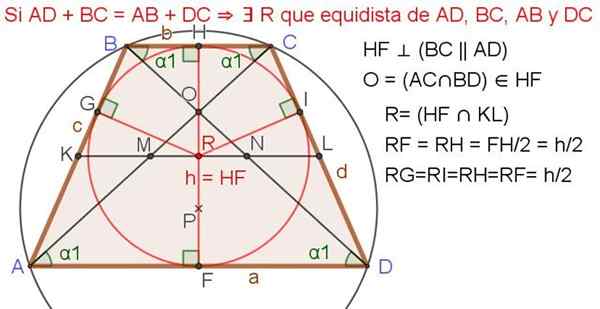Figur 4. Trapes med registrerad omkrets. Källa: f. Zapata.

Följande egenskaper gäller när isosceles trapezoid har en registrerad omkrets (se figur 4 ovan):

16.- Kl = ab = dc = (ad + bc)/2

17.- Diagonalerna skärs i rätt vinkel: AC ⊥ BD

18.- Höjden är densamma som medianen: hf = kl, det vill säga h = m.

19.- Höjdens kvadrat är lika med produkten från baserna: h² = Bc⋅ad

tjugo.- Under dessa specifika förhållanden är trapesområdet lika med höjden eller produkten från basen: området = h² = Bc⋅ad.

Formler för att bestämma ena sidan, kända de andra och en vinkel

Känd en bas, sidan och en vinkel, den andra basen kan bestämmas av:

a = b + 2c cos a

B = A - 2C COS a

Om basens längd är känd som känd och en vinkel så är längden på båda sidor:

Det kan tjäna dig: Fermat Limit: Vad består och övningar löst

C = (a - b) / (2 cos a)

Beslutsamhet på ena sidan, kända de andra och en diagonal

A = (D₁² - c²)/ B;

B = (D₁² - c²)/ till 

C = √ (D₁² - A⋅b)

Var d₁ Det är längden på diagonalerna.

Bas från höjden, området och den andra basen

a = (2 a)/h - b

b = (2 a)/h - a

Kända tillbaka baserna, området och en vinkel

C = (2a) /[(a + b) sin α]

Känd i sidled medianen, området och en vinkel

C = a / (m.sin α)

Känd höjd sidorna

H = √ [4 c² - (A - B)²]

Känd höjd en vinkel och två sidor

H = TG α⋅ (A - B)/2 = C . synd

Kända diagonaler alla sidor eller två sidor och en vinkel

d₁ = √ (c²+ a b)

d₁ = √ (a²+ c² - 2 a c cos α)

d₁ = √ (b² + c²- 2 b c cos β)

Isosceles triangel omkrets 

P = A + B + 2C

Isosceles trapezoidområde

Det finns flera formler för att beräkna området, beroende på de data som är kända. Följande är det mest kända, beroende på baser och höjd:

A = h⋅ (a + b)/2

Och dessa andra kan också användas:

-Om sidorna är kända

A = [(a +b)/4] √ [4c² - (A - B)²]

-När du har två sidor och en vinkel

A = (b + c cos α) c Sen α = (a - c cos a) c Sen a a a

-Om radien för den registrerade omkretsen är känd och en vinkel

A = 4 r² / Sin α = 4 r² / Sin β

-När baserna och en vinkel är känd

A = A⋅B / sin α = A⋅B / SEN ß 

-Om trapes kan registreras en omkrets

A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b)/2

-Kända diagonaler och vinkel som bildas med varandra

A = (D₁²/2) SEN γ = (D₁² / 2) Sen Δ 

-När du har sidan, medianen och en vinkel

A = mc.sin α = mc.Sen β

Omskriven omkretsradio

Endast isosceles trapezoider har en omskriven omkrets. Om huvudbasen är känd, sidan C och Diagonal D₁, Då är radien R för omkretsen som passerar genom trapes fyra vertikaler:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p -d₁)]]

Där p = (a + c + d₁) / 2

Exempel på användning av isosceles trapezoid

Isosceles trapezoid visas inom designområdet, som ses i figur 2. Och här har vi några ytterligare exempel:

I arkitektur och konstruktion

De antika incorna kände till isoscelerna trapezoid och använde den som ett konstruktionselement i detta fönster i Cuzco, Peru:

Figur 5 . Fönster med en trapesformad form av Coricancha, Cuzco. Källa: Wikimedia Commons.

Och här visas trapezoiden igen i samtalet Trapesformad ark, Ett ofta använt material i konstruktionen:

Figur 6. Trapezoidal metallplåt skyddar tillfälligt fönstren i en byggnad. Källa: Wikimedia Commons.

I design

Vi såg redan att isosceles trapezoid visas i vardagliga föremål, inkluderande livsmedel som denna chokladkaka:

Figur 7. Chokladkaka vars ansikten är formade som liksiktiga. Källa: PXFuel.

Löst övningar

- Övning 1

En isosceles trapezoid är baserad än 9 cm, bas mindre än 3 cm och dess diagonaler 8 cm vardera. Beräkna:

Det kan tjäna dig: allmän parabola -ekvation (exempel och övningar)

a)

b) höjd

c) omkrets

d) ärea

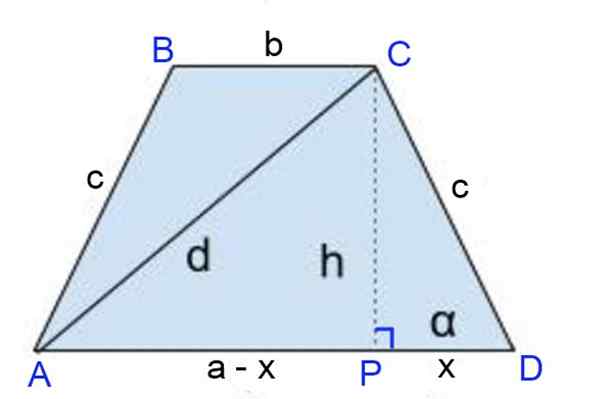Figur 8. Schema för övning 1. Källa: f. Zapata

Lösning till

Höjden CP = H ritas, där höjden på höjden definierar segmenten:

Pd = x = (a-b)/2 och 

AP = A - X = A - A/2 + B/2 = (A + B)/2.

Genom Pythagoras -teoremet till DPC -rektangeln:

c² = h² + (A - B)² /4

Och även till APC -rektangeln:

d² = h² + Ap² = h² + (A+B)² /4

Slutligen subtraheras en medlem, den första ekvationen för den första och förenklar:

d² - c² = ¼ [(a+b)² - (A-b)²] = ¼ [(A+B+A-B) (A+B-A+B)]

d² - c² = ¼ [2a 2b] = A B

c²= D² - A B ⇒ C = √ (D² - A B) = √ (8² - 9⋅3) = √37 = 6,08 cm

Lösning B

h² = D² - (A+B)² /4 = 8² - (12² / 2² ) = 8² - 6² = 28

H = 2 √7 = 5,29 cm

Lösning C

Omkrets = A + B + 2 C = 9 + 3 + 2⋅6,083 = 24,166 cm

Lösning D

Area = h (a+b)/2 = 5,29 (12)/2 = 31,74 cm

- Övning 2

Det finns en isosceles trapezoid vars största bas är dubbelt den mindre och dess minsta bas är lika med höjden, som är 6 cm. Bestämma:

a) sidan av sidan

b) omkrets

c)

d) vinklar

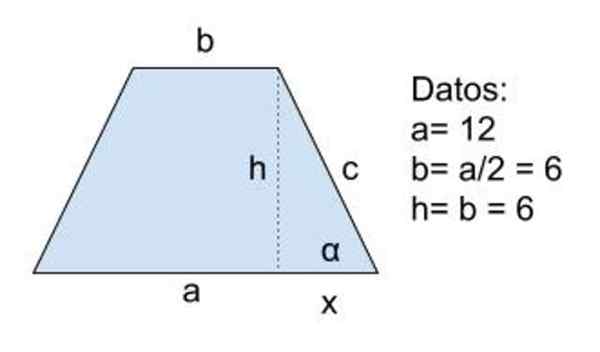Figur 8. Schema för övning 2. Källa: f. Zapata

Lösning till

Data: a = 12, b = a/2 = 6 och h = b = 6

Vi fortsätter på detta sätt: höjden h ritas och Pythagoras teorem appliceras på hypotenuse -triangeln "C" och Catetos H och X:

c² = h²+Xc²

Då måste du beräkna höjdvärdet från data (H = B) och Cateto X: 

a = b + 2 x ⇒ x = (a-b)/2

Ersätta de tidigare uttryck du har:

c² = B²+(A-b)²/2²

Nu introduceras och förenklas numeriska värden:

c² = 62+ (12-6) 2/4

c² = 62 (1+¼) = 62 (5/4)

Erhållande:

C = 3√5 = 6,71 cm

Lösning B

Omkretsen p = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Lösning C

Området baserat på basens höjd och längd är:

A = h⋅ (a + b)/2 = 6⋅ (12 + 6)/2 = 54 cm²

Lösning D

Vinkeln a som bildar sidan med huvudbasen erhålls genom trigonometri:

Solbränna (α) = h / x = 6/3 = 2

α = arctan (2) = 63,44º

Den andra vinkeln, som bildar sidan med den mindre basen är ß, som är kompletterande av α:

β = 180º - α = 180º - 63,44º = 116,56º

Referenser

1. OCH. TILL. 2003. Geometrielement: med övningar och kompassgeometri. University of Medellin.
2. Campos, f. 2014. Matematik 2. Patria Redaktionsgrupp.
3. Freed, K. 2007. Upptäck polygoner. Utbildningsföretag.
4. Hendrik, V. 2013. Generaliserade polygoner. Birkhäuser.
5. Iriger. Matematik första termin Tacaná. Iriger.
6. Jr. Geometri. 2014. Polygoner. Lulu Press, Inc.
7. Miller, Heeren och Hornsby. 2006. Matematik: resonemang och tillämpningar. 10: e.  Utgåva. Pearson Education.
8. Patiño, m. 2006. Matematik 5. Redaktionell progreso.
9. Wikipedia. Trapets. Återhämtad från: är.Wikipedia.com