Kontinuerliga variabla egenskaper, exempel och övningar

De Kontinuerlig variabel Det är en som kan ta ett oändligt antal numeriska värden mellan två givna värden, även om dessa två värden är godtyckligt nära. De används för att beskriva mätbara attribut; till exempel höjd och vikt. Värdena som tagits av en kontinuerlig variabel kan vara rationella siffror, verkliga siffror eller komplexa siffror, även om detta sista fall är mindre ofta i statistik. 

Det huvudsakliga kännetecknet för kontinuerliga variabler är att mellan två rationella eller verkliga värden alltid kan hittas, och mellan den andra och den första kan hitta ett annat värde, och så på obestämd tid.

Figur 1. Kurvan representerar en kontinuerlig fördelning och staplarna är en diskret. Källa: Pixabay

Anta till exempel viktvariabeln i en grupp där den största vikten har 95 kg och den lägsta 48 kg vikten; Det skulle vara variabeln och antalet möjliga värden är oändligt.

Till exempel kan mellan 50,00 kg och 50,10 kg vara 50,01. Men mellan 50,00 och 50,01 kan åtgärden vara 50,005. Det är en kontinuerlig variabel. Å andra sidan, om en enda decimal noggrannhet i de möjliga viktmätningarna fastställdes, skulle variabeln vara diskret.

Kontinuerliga variabler tillhör kategorin kvantitativa variabler, eftersom de har ett numeriskt värde associerat. Med detta numeriska värde är det möjligt att utföra matematiska operationer som sträcker sig från aritmetik till metoderna för infinitesimal beräkning. 

[TOC]

Exempel

De flesta variabler i fysik är kontinuerliga variabler, bland dem kan vi namnge: längd, tid, hastighet, acceleration, energi, temperatur och andra.

Kontinuerliga variabler och diskreta variabler

I statistik kan olika typer av variabler definieras, både kvalitativa och kvantitativa. Kontinuerliga variabler tillhör den sista kategorin. Hos dem är det möjligt att utföra aritmetiska och beräkningsoperationer.

Till exempel variabeln h, Motsvarande personer med höjd mellan 1,50 m och 1,95 m, är det en kontinuerlig variabel. 

Låt oss jämföra denna variabel med denna andra: antalet gånger som är dyrt vid lanseringen av en valuta, som vi kommer att ringa n.

Variabeln n Du kan dock ta värden mellan 0 och oändligheten n Det är inte en kontinuerlig variabel eftersom den inte kan ta värdet 1,3 eller 1,5, för mellan värden 1 och 2 finns det ingen annan. Detta är ett exempel på Diskret variabel.

Utövande av kontinuerliga variabler

Tänk på följande exempel: En maskin producerar fosformatchningar och packar dem i sin låda. Två statistiska variabler definieras:

Kan tjäna dig: isobarisk process: formler, ekvationer, experiment, övningar

Variabel 1: l = ploslängd.

Variabel 2: n = antal grisar per låda.

Den nominella matchens längd är 5,0 cm med en 0,1 cm tolerans. Antalet grisar per låda är 50 med en tolerans på 3.

a) Ange intervallet av värden som kan ta L och N.

b) Hur många värden kan du ta L?

c) Hur många värden kan du ta n?

Säga i båda fallen om det är en diskret eller kontinuerlig variabel.

Lösning

Värdena på L De förstås i intervallet [5,0-0,1; 5,0+0,1]; det vill säga att värdet av L är i intervall [4,9 cm; 5.1 cm] och variabeln L Du kan ta oändliga värden mellan dessa två mått. Det är då en kontinuerlig variabel.

Värdet på variabeln n är i intervallet [47; 53]. Variabeln n Det kan bara ta 6 möjliga värden i toleransintervallet, det är då en diskret variabel.

Utövande av sannolikhetsfördelning

Om förutom att de är kontinuerliga har värdena som tagits av variabeln associerat en viss sannolikhet för händelse, är det en Kontinuerlig slumpmässig variabel. Det är mycket viktigt att skilja om variabeln är diskret eller kontinuerlig, eftersom probabilistiska modeller som är tillämpliga på varandra är olika.

En kontinuerlig slumpmässig variabel definieras fullständigt när värdena de kan anta är kända, och sannolikheten för att var och en av dem måste hända.

-Övning 1 av sannolikheter

Matches -fabriken gör dem på ett sådant sätt att pinnarnas längd alltid är mellan värden på 4,9 cm och 5,1 cm och noll av dessa värden. Det finns sannolikheten för att få en pinne som mäter mellan 5,00 och 5,05 cm, även om vi också kunde extrahera en av 5.0003 cm. Är dessa värden lika troliga?.

Kan tjäna dig: Relativ densitet: Beräkning, exempel, övningar

Lösning

Anta att sannolikhetstätheten är enhetlig. Därefter listas chansen att hitta en fosfor med en viss längd:

-Att en fosfor är i sortimentet [4,9; 5,1] har sannolikhet = 1 (eller 100%), eftersom maskinen inte tar matcher ur dessa värden.

-Att hitta en fosfor som är mellan 4,9 och 5,0 har sannolikhet = ½ = 0,5 (50%), eftersom det är hälften av längden i längden.

-Och sannolikheten för att matchen har längd mellan 5,0 och 5,1 är också 0,5 (50%)

-Det är känt att det inte finns några fosforpinnar som har en längd mellan 5,0 och 5,2. Sannolikhet: noll (0%).

Sannolikheten för att hitta en pinne i ett visst område

Låt oss nu observera följande sannolikheter P för att få pinnar vars längd är mellan L₁ och jag₂:

 P = (l₂ -l₁) /(L_Max - L_min)

-P att en match har en längd mellan 5,00 och 5,05 betecknas som P ([5.00; 5.05]):

P ([5.00; 5.05]) = (5.05 - 5.00)/(5.1 - 4.9) = 0,05/0,2 = ¼ = 0,25 (25%)

-P att cerrillo har längd mellan 5,00 och 5,01 är:

P ([5.00; 5.01]) = (5.00 - 5.01)/(5.1 - 4.9) = 0,01/0,2 = 1/20 = 0,05 (5 %)

-P att cerrillo har längden mellan 5 000 och 5 001 är ännu lägre:

P (5 000; 5,001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)

Om vi ​​fortsätter att minska intervallet för att närma sig mer och mer till 5,00, är ​​sannolikheten för att en pinne har exakt 5,00 cm noll (0%). Vad vi har är sannolikheten för att hitta en match inom ett visst intervall.

Sannolikheten för att hitta flera pinnar i ett visst område

Om händelserna är oberoende är sannolikheten för att två pinnar är inom ett visst intervall produkten av deras sannolikheter.

-Sannolikheten för att två pinnar är mellan 5,0 och 5,1 är 0,5*0,5 = 0,25 (0,25%)

-Sannolikheten för att 50 pinnar är mellan 5,0 och 5,1 är (0,5)^50 = 9 × 10^-16, det vill säga nästan noll.

-Sannolikheten för att 50 pinnar är mellan 4,9 och 5.1 är (1)^50 = 1 (100%)

-Övning 2 av sannolikheter

I föregående exempel gjordes antagandet att sannolikheten är enhetlig i det givna intervallet, men det är inte alltid fallet.

Kan tjäna dig: hydrostatisk tryck: formel, beräkning, exempel, övningar

När det gäller den verkliga maskinen som producerar pinnarna är möjligheten att pinnen är i det centrala värdet större än i ett av de extrema värdena. Från den matematiska synvinkeln modelleras detta med en funktion f (x) känd som sannolikhetstäthet.

Sannolikheten för att åtgärden är mellan A och B beräknas genom den definierade integralen av funktionen F (x) mellan a och b. 

Som ett exempel, anta att vi vill hitta funktionen f (x), som representerar en enhetlig fördelning mellan värden 4.9 och 5.1 i övning 1. 

Om sannolikhetsfördelningen är enhetlig är f (x) lika med konstant c, vilket bestäms med att ta integralen mellan 4,9 och 5,1 i c. Eftersom denna integral är sannolikheten, så måste resultatet vara 1.

figur 2. Enhetlig sannolikhetstäthet. (Egen utarbetande)

Vilket innebär att C är värd 1/0,2 = 5. Med andra ord är den enhetliga sannolikhetsdensitetsfunktionen f (x) = 5 om 4,9≤x≤5.1 och 0 ur detta intervall. Figur 2 visar en enhetlig sannolikhetsdensitetsfunktion.

Obs! Som i intervaller med samma bredd (till exempel 0,02) är sannolikheten densamma i mitten som i slutet av det kontinuerliga variabla intervallet L (Pickle längd).

En mer realistisk modell skulle vara en sannolikhetsdensitetsfunktion som följande:

-f (x) = -750 ((x-5.0)^2-0.01) om 4,9 an 5,1

-0 Utanför detta sortiment 

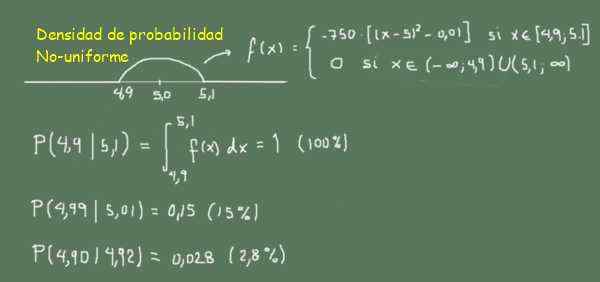Figur 3. Icke -enhetlig sannolikhetsdensitetsfunktion. (Egen utarbetande)

I figur 3 kan det observeras som sannolikheten för att hitta pinnar mellan 4,99 och 5,01 (bredd 0,02) är större än att hitta pinnar mellan 4,90 och 4,92 (bredd 0,02)

Referenser

1. Dinov, Ivo. Diskreta slumpmässiga variabler och sannolikhetsfördelningar. Återhämtat sig från: stat.Ucla.Edu
2. Diskreta och kontinuerliga slumpmässiga variabler. Återhämtat sig från: ocw.mit.Edu
3. Diskreta slumpmässiga variabler och sannolikhetsfördelningar. Återhämtat sig från: hemsida.DDMS.Uiowa.Edu
4. H. Peshro. Introduktion till sannolikhet. Återhämtat sig från: sannolikhetskurs.com
5. Mendenhall, W. 1978. Statistik för administration och ekonomi. Ibero -amerikansk redaktionsgrupp. 103-106.
6. Slumpmässiga variabla problem och sannolikhetsmodeller. Återhämtat sig från: ugr.är.
7. Wikipedia. Kontinuerlig variabel. Återhämtat sig från Wikipedia.com
8. Wikipedia. Statistisk variabel. Återhämtat sig från Wikipedia.com.