X kvadrat

Vi förklarar vad som är x kvadrat, dess egenskaper, exempel och övningar löst

Området på en kvadrat av "x" -sidan är x kvadrat. Källa: f. Zapata.

Den algebraiska driften av "X kvadrat"Det utförs genom att multiplicera beloppet" x "med sig själv två gånger. Det är en del av potentieringsoperationerna, och i matematiska symboler uttrycks det på detta sätt:

x ∙ x = x²

Detta är ett särskilt fall av empowerment, där "x" representerar bas Och "2" är exponent. Om termen X i en operation visas², Det läser exakt som "X Squared" eller "X Square Elevated".

Naturligtvis är andra exponenter möjliga, till exempel om exponenten är 3, är kraften skriven som:

x ∙ x ∙ x = x³

Och läs som "x till de tre", "x upp till kuben" eller helt enkelt "x till kuben".

I allmänhet kan den exponent som basen är hög är valfritt, kallas "n" och i så fall skrivs motsvarande kraft:

xⁿ = x ∙ x ∙ x ∙ ... ∙ x

Här indikerar de suspensiva punkterna att "x" måste multipliceras av sig själv "n", det vill säga så många gånger som exponenten indikerar det.

Några enkla exempel på "x kvadrat", med siffror, är följande:

3² = 3 ∙ 3 = 9

(−4)² = (−4) ∙ (−4) = 16

Senare beskrivs olika applikationer för vilka det är nödvändigt.

Potentieringsegenskaper

I allmänhet är produkten av alla belopp med sig själv, n gånger, den kallas potentiering. Beräkningen av X Squared är endast ett visst fall av potentiering, två andra fall visas när du vill höja ett belopp till exponent 1 och få ett resultat samma belopp:

Kan tjäna dig: exponenters lagar

Eftersom dessa operationer är ofta, för att arbeta med baser och exponenter följs några enkla driftsregler, kallas Exponenternas lagar, som listas nedan:

Exponenternas lagar

I det följande är "X" basen och "n" och "m" är exponenterna.

1.- Produkt av lika baskrafter

Genom att multiplicera två (eller fler) krafter med lika bas erhålls basen som är upphöjd till summan av exponenterna:

xⁿ∙ x^m = x^n+m

När det gäller X High tillämpas denna regel enligt följande och ersätter N och M för 1:

x¹∙ x¹ = x¹⁺¹ = x²

2.- Powers Division of Equal Base

Genom att dela krafter i samma bas erhålls basen, höjs till subtraktionen mellan respektive exponenter för telleren och nämnaren:

xⁿ ÷ x^m = x^N-m

Eftersom divisionen med 0 inte är definierad måste den uppfyllas förutsatt att x ≠ 0.

3.- Maktens kraft

Resultatet av kraften hos en kraft är lika med basen som är upphöjd till produkten av exponenterna:

(x^m)ⁿ = x^m∙n

Det kan erhållas igen x kvadrat, när man gör m = 1 och n = 2:

(x¹)² = x^1∙2 = x²

4.- Negativ exponent

För negativa exponenter är operationen som ska utföras:

När x ≠ 0. Observera att kraften i detta fall blir en bråkdel med en teller lika med 1.

5.- Fraktionerad exponent

Fraktionella exponenter kan skrivas som basens nth rot:

Under förutsättning att n skiljer sig från 0. Detta värde blir rotindexet, medan M blir exponenten för mängden under roten, vilket i detta fall är x.

Kan tjäna dig: vad är riktlinjen? (Geometri)

Produkter och kvoter i olika baser

När du måste förbättra produkter och kvoter för olika "X" och "Y" -baser följs dessa regler:

1.- Produkt

För att utföra denna kraft höjs varje belopp till exponenten N och den resulterande produkten upprättas:

(x ∙ y)ⁿ = xⁿ ⋅ ochⁿ

2.- Kvotförhållandet

Återigen måste varje belopp tas upp till exponenten n separat och fastställa kvoten som resulterar efter regeln att mängden "y" skiljer sig från 0, i fallet med positivt "n":

(x ÷ y)ⁿ = xⁿ ÷ yⁿ

När "n" är negativ måste försiktighet vidtas, på grund av egendom 4 i föregående avsnitt, blir telleren en nämnare. I detta fall måste båda beloppen vara annorlunda än 0, eftersom uppdelningen med 0 måste undvikas till varje pris.

Exempel

Exempel 1: Squares of Natural Numbers

Kvadrarna i de första tio naturliga siffrorna är:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Exempel 2: kvadratet med negativa siffror

Kvadratet med ett negativt antal är alltid positivt, eftersom två mängder lika tecken multipliceras därför:

(-x) · (-x) = x ∙ x = x²

Till exempel:

(-2) · (-2) = (-2)² = 4

Exempel 3: kvadrat för summan och skillnaden

Det är ofta nödvändigt att beräkna kvadratet för summan av två mängder, eller dess skillnad, verksamhet som ingår i kategorin anmärkningsvärda produkter.

Operationen löses med indikationerna och hjälp av distribuerande egendom:

Summan

Låt två "X" och "Y" -mängder, och du vill hitta kvadratet för dess summa (x + y)²:

Kan tjäna dig: hierarki av verksamheten

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + och²

Detta uttryck läser så här: "Square of the First, plus den dubbla produkten av den första för det andra plus torget på det andra".

Skillnadskvadrat

Det är löst analogt, men med hänsyn till det negativa tecknet:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ och + och²

Exempel 4: Området på ett fyrkant

Torget är en 4 -sidad polygon, som har samma mått. Låt ℓ vara sidmätningen, sedan ges område A i figuren av:

A = ℓ²

Exempel 5: Pythagoras teorem

Detta sats gäller för rektangel trianglar, de på vilka två av dess sidor bildar rak vinkel. Dessa sidor är kända som "kategorier" och den återstående sidan är "hypotenus".

Satsen konstaterar att torget för hypotenusa är lika med summan av kvadrarna i kategorierna. Satsen kallar "A" och "B" till kategorierna och "C" till hypotenusen och är skriven som:

c² = a² + b²

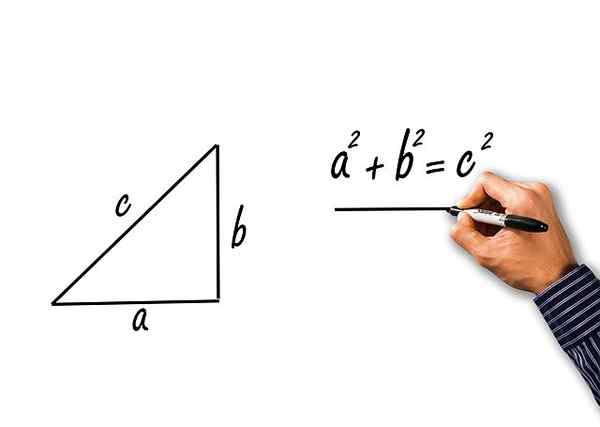Pythagoras teorem för en rektangel triangel av katter A och B, och hypotenusa c

Löst övningar

Övning 1

Beräkna kvadratet på hypotenusen vars ben mäter 3 och 5 enheter.

Lösning

Enligt Pythagoras teorem är torget för hypotenus:

c² = a² + b²

Ersätta värdena:

c² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Övning 2

Bestäm området på en sidokylt ℓ = 6 cm

Lösning

A = ℓ² = (6 cm)² = 36 cm²