Tyngdkraft vad det är, hur det mäts och övningar

De Tyngdkraftsacceleration o Gravitationsacceleration definieras som intensiteten i landgravitationsfältet. Det vill säga den kraft som detta utövar på alla objekt per massaenhet.

Det betecknas med den redan bekanta bokstaven G och dess ungefärliga värde i närheten av jordens yta är 9.8 m/s². Detta värde kan uppleva små variationer med geografisk latitud och även med höjden med avseende på havsnivå.

Astronaut i rymden paseo på jordens yta. Källa: Pixabay

Acceleration av tyngdkraften, förutom att ha den nämnda storleken, har riktning och mening. Det riktas verkligen vertikalt mot jordens centrum.

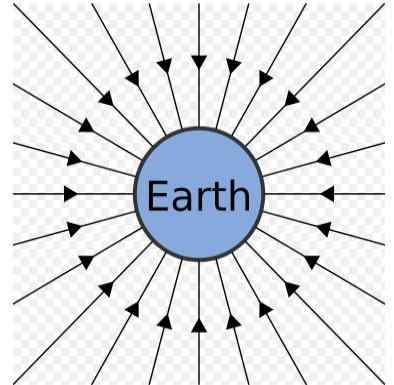Jordens gravitationsfält. Källa: Källa: SJLEGG [Public Domain]

Jordens gravitationsfält kan representeras som en uppsättning radiella linjer som pekar på mitten, vilket kan ses i föregående figur.

[TOC]

Vad är tyngdens acceleration?

Värdet på tyngdkraftens acceleration i jorden eller på någon annan planet motsvarar intensiteten på gravitationsfältet det producerar, som inte beror på de föremål som finns runt den, utan bara på sin egen massa och dess radie.

Ofta definieras ofta tyngdkraften som den acceleration som upplever av något objekt i fritt fall i närheten av jordens yta.

I praktiken är detta det som nästan alltid händer, som vi kommer att se i följande avsnitt, där Newtons universella gravitationslag kommer att användas.

Det sägs att Newton upptäckte denna berömda lag medan han mediterade på kroppens fall under ett träd. När han kände äpplets slag i huvudet visste han omedelbart att kraften som gör att äpplet faller är densamma som gör månen förbi runt jorden.

Den universella gravitationslagen

En viss eller inte Apple -legenden, Newton, insåg att storleken på gravitationsattraktionskraften mellan två föremål, till exempel mellan jorden och månen, eller jorden och äpplet, var tvungen att bero på massorna av dessa:

Där m₁ Det kan vara jordens massa och m_2, Månens massa eller äpple. En större massa, större attraktion finns bland kropparna. Men på mer avstånd, mindre kraft, eftersom detta måste vara omvänt proportionellt mot torget av avståndet r som skiljer dem:

Kan tjäna dig: Elastiska chocker: I en dimension, specialfall, övningar

Detta är sant oavsett hur stora eller små är massorna i fråga. Genom att kombinera dessa fakta skulle tyngdkraften förbli på detta sätt:

En konstant av proportionalitet behövs för att ha denna empiriska lag redo. Newton beräknade konstanten G, så att formeln beskriver med alla precision rörelserna hos himmelkropparna i skalets skala och därefter:

Där g = 6.67 x 10^-elva N.m²/kg²

Gravitationella egenskaper

Gravitationskraften är alltid attraktiv; det vill säga de två kroppar som den påverkar lockas till varandra. Det motsatta är inte möjligt, eftersom himmelkropparnas banor är stängda eller öppna (till exempel kometer) och en repulsionskraft aldrig kan producera en stängd bana. Då lockar massorna alltid, vad som händer.

En ganska bra inställning till jordens verkliga form (m₁) Och månen eller äpplet (m₂) är att anta att de har en sfärisk form. Följande figur är en representation av detta fenomen.

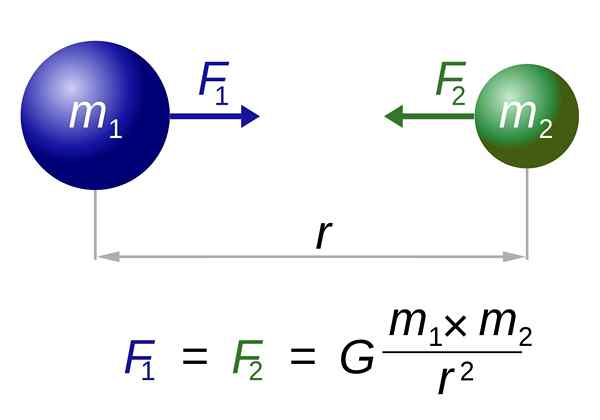Newtons universella gravitationslag. Källa: I, Dennis Nilsson [CC av 3.0 (https: // CreativeCommons.Org/licenser/av/3.0)]

Här är båda kraften som utövas m₁ Om M₂, Som den som utövar m₂ Om M₁, både med lika stor storlek och riktad längs linjen som går med i centren. De avbryts inte, eftersom de tillämpas på olika objekt.

I alla följande avsnitt antas att föremål är homogena och sfäriska, därför sammanfaller dess tyngdkraft med dess geometriska centrum. All koncentrerad massa kan antas just där.

Hur mäts tyngdkraften på olika planeter?

Tyngdkraften kan mätas med en liemeter, en apparat som tjänar till att göra allvar mätt i geofysiska gravimetriska undersökningar. De är för närvarande mycket mer sofistikerade än originalen, men i början var de baserade på pendeln.

Pendeln består av ett tunt, lätt och oförstörande rep av längd l. Ett av dess ändar är fixerade på ett stöd och den andra hänger en massa m.

När systemet är i jämvikt hänger degen vertikalt, men när den är separerad från det börjar det att svänga med en svängrörelse. Gravity är ansvarig för det. För allt som följer är det giltigt att anta att tyngdkraften är den enda kraften som verkar på pendeln.

Kan tjäna dig: aerostatisk ballong: historia, egenskaper, delar, hur det fungerar

Perioden för svängningen av pendeln för små svängningar, ges av följande ekvation:

Kraften T beror inte på massan, men på längden på L och värdet på G. Square Båda medlemmarna i ekvationen är:

Relationen mellan T² och L Det är linjärt: en linje i formen y = a.x, där värdet på till, Linjens lutning är exakt (4π²/g).

Experiment för att bestämma värdet på g

Materiel

- 1 Metallfärit.

- Rep med flera olika längder, minst 5.

- Måttband.

- Transportband.

- Kronometer.

- Ett stöd för att sätta pendeln.

- Milimetreringspapper eller datorprogram med kalkylblad.

Procedur

1. Välj en av strängarna och montera pendeln. Mät längden på repet + sfärens radie. Detta kommer att vara längden l.
2. Ta bort pendeln från jämviktspositionen cirka 5 grader (id med transportören) och lämna den oscillerad.
3. Samtidigt starta stoppuret och mät tiden för 10 svängningar. Skriv ner resultatet.
4. Upprepa den tidigare proceduren för de andra längderna.
5. Hitta den tid som tar pendeln för att utföra en svängning (dela vart och ett av de tidigare resultaten med 10).
6. Kvadrera varje värde som erhålls, erhålla t²
7. Grafera varje värde på t i millimeterpapperet² På den vertikala axeln, mot respektive värde på l på den horisontella axeln. Var förenlig med enheterna och glöm inte att ta hänsyn till felet i uppskattningen av de använda instrumenten: Metriska tejp och stoppur.
8. Rita den bästa linjen som passar de grafiska punkterna.
9. Hitta lutningen m av denna linje med två punkter som tillhör den (inte nödvändigtvis experimentella punkter). Lägg till experimentfelet.
10. Ovanstående steg kan utföras med ett kalkylblad och alternativet att bygga och justera en rak linje.
11. Från sluttningen till rensa värdet på g Med deras respektive experimentella osäkerhet.

Standardvärde på g På jorden, på månen och på Mars

Standardvärdet för tyngdkraften på jorden är: 9.81 m/s², vid 45 norra latitud och vid havsnivån. Eftersom jorden inte är en perfekt sfär, värdena på g De varierar något och är större i polerna och minderåriga i Ecuador.

De som vill veta värdet på sin ort kan hitta det uppdaterat på webbplatsen för Metrology Institute of Germany PTB (Physikalisch-Technische Bundesanstalt), i avsnittet Gravity Information System (KRITA).

Det kan tjäna dig: Director Vector: Straight Equation, Löst övningar

Tyngdkraften på månen

Månens gravitationsfält har bestämts genom analys av radiosignalerna för rymdprober som kretsar runt satelliten. Dess värde på månytan är 1.62 m/s²

Svårighetsgraden i Mars

Värdet av g_P För en planet beror det på dess massa m och dess radie på följande sätt:

Därför:

För planeten Mars är följande data tillgängliga:

M = 6 4185 x 10²³ kg

R = 3390 km

G = 6.67 x 10^-elva N.m²/kg²

Med dessa data vet vi att Mars är 3.71 m/s². Naturligtvis kan samma ekvation tillämpas på måndata eller någon annan planet och därmed uppskatta värdet på dess svårighetsgrad.

Löst övning: äpplet som faller

Anta att både jorden och ett äpple har en sfärisk form. Jordens massa är m = 5,98 x 10²⁴ kg och dess radie är r = 6,37 x 10⁶  m. Äpplets massa är m = 0.10 kg. Anta att det inte finns någon annan kraft utom tyngdkraften. Från Newtons universella gravitationslag:

a) Gravitationskraften som utövas på äpplet.

b) Applansen som upplever när man släpper ut det från en viss höjd, enligt Newtons andra lag.

Lösning

a) Äpplet (antagna sfäriska, precis som jorden) har en mycket liten radie jämfört med den markbundna radien och är nedsänkt i sitt gravitationsfält. Följande siffra är inte uppenbarligen, men det finns ett schema för gravitationsfältet g, och strengh F utövas av jorden på äpplet:

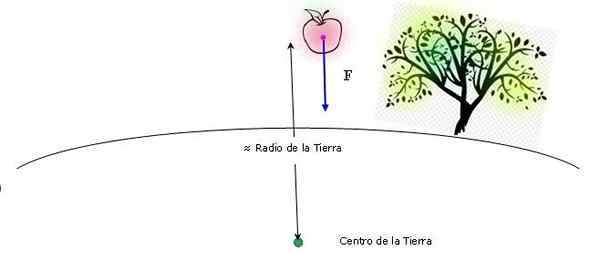Schema som visar äpplets fall i jordens närhet. Både storleken på äpplet och höjden på hösten är föraktlig. Källa: Självgjord.

Vid tillämpning av Newtons universella gravitationslag kan avståndet mellan centren betraktas som ungefär samma värde som jordens radie (höjden från vilken äpplet faller också är försumbar jämfört med markradie). Därför:

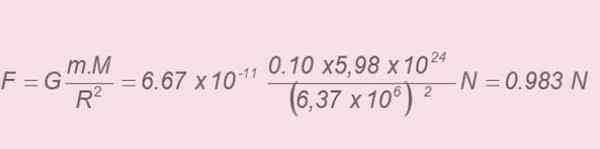
b) Enligt Newtons andra lag är storleken på den kraft som utövas på äpplet:

F = ma = mg

Vars värde är 0.983 N, enligt föregående beräkning. Utjämning av båda värdena och sedan rensning av accelerationens storlek erhålls:

mg = 0.983 n

G = 0.983 n/0.10 kg = 9.83 m/s²

Detta är ett mycket bra tillvägagångssätt för tyngdkraftsvärdet.

Referenser

1. Giancoli, D. (2006). Fysik: Principer med applikationer. Sjätte upplagan. Prentice hall. 118-122.
2. Hewitt, Paul. (2012). Konceptuell fysisk vetenskap. Femte upplagan. Pearson. 91 - 94.
3. Rex, a. (2011). Fysikens grunder. Pearson. 213-221.