Båge (geometri) mått, typer av bågar, exempel

han rosett, I geometri är det alla böjda linjer som ansluter två punkter. En krökt linje, till skillnad från en rak linje, är den vars riktning är annorlunda vid varje punkt av samma. Det motsatta av en båge är ett segment, eftersom detta är en rak sektion som går med i två poäng.

Bågen som oftast används i geometri är omkretsbågen. Andra bågar med vanligt bruk är Parabolic Arch, Elliptical Arch och Catenary Arch. Bågformen används också ofta i arkitektur som ett dekorativt element och strukturellt element. Detta är fallet med lintarna på dörrar och fönster, såväl som broar och akvedukter.

Figur 1. Rainbow är en krökt linje som går med två punkter i horisonten. Källa: Pixabay

[TOC]

Bågen och dess mått

Måttet på en båge är dess längd, som beror på vilken typ av kurva som ansluter de två punkterna och platsen för dem.

Längden på en cirkulär båge är en av de enklaste att beräkna, eftersom den fulla båglängden eller omkretsen av en cirkel är känd.

Omkretsens omkrets är två pi gånger din radio: P = 2 π r. Att veta detta, om du vill beräkna längden s av en cirkulär vinkelbåge a (mätt i radianer) och radio R, En andel tillämpas:

(S / P) = (α / 2 π)

Sedan rensning s av det tidigare uttrycket och ersätter omkretsen p genom dess uttryck beroende på radio R, Du har:

S = (a / 2 π) p = (a / 2 π) (2 π r) = α r.

Det vill säga måttet på en cirkulär båge är produkten från dess vinkelöppning av den cirkulära bågradie.

För en båge på ett allmänt sätt är problemet mer komplicerat, till den punkten att antikvitetens stora tänkare hävdade att det var en omöjlig uppgift.

Det kan tjäna dig: vad är algebraiska uttryck och vilka är de vanligaste?

Det var inte förrän tillkomsten av den differentiella och integrerade kalkylen 1665, att problemet med mått på alla bågar löstes tillfredsställande. 

Innan uppfinningen av den differentiella beräkningen kunde endast lösningar hittas genom användning av polygonal linje eller omkretsbågar som närmade sig den sanna bågen, men dessa lösningar var inte exakta. 

Typer av bågar

Ur geometriens synvinkel klassificeras bågarna enligt den böjda linjen som går med två punkter på planet. Det finns andra klassificeringar enligt dess arkitektoniska användning och form.

Cirkulärbåge

När linjen som ansluter två punkter i planet är en bit omkrets av en viss radie, finns det en cirkulär båge. Figur 2 visar en cirkulär båge av radie r som ansluter punkter a och b.

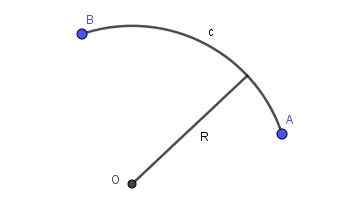figur 2. Radio r cirkulär båge som ansluter punkt A och B. Förberedd av Ricardo Pérez.

Båge

Liknelsen är banan som följer ett objekt som har kastats i luften i sned form. När kurvan som ansluter sig till två punkter är en liknelse, finns det en parabolisk båge som den som visas i figur 3.

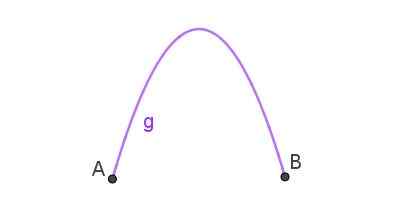Figur 3. Parabolisk båge som ansluter poäng a och b. Förberedd av Ricardo Pérez.

Detta är den form som antar vattenstrålen som kommer ut ur en slang som pekar upp. Den paraboliska bågen kan observeras i vattenkällorna.

Figur 4. Parabolisk båge bildad av vatten från en källa i Dresden. Källa: Pixabay.

Kedjebåge

Catenary Arc är en annan naturlig båge. Catenary är den kurva som naturligt bildas när en kedja eller ett rep hänger bekvämt från två separata punkter.

Kan tjäna dig: Vilka är elementen i en vinkel?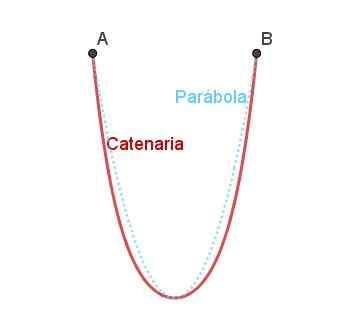 Figur 5. Catenary Arc och jämförelse med den paraboliska bågen. Förberedd av Ricardo Pérez.

Catenary liknar parabolen, men det är inte exakt samma som det kan noteras i figur 4.

Den inverterade catenary -formade bågen används i arkitekturen som ett strukturellt element i hög kompressionsresistens. I själva verket kan det demonstreras att det är den mest resistenta bågtypen bland alla möjliga former. 

För att bygga en solid catenary båge, bara formen på ett rep eller kedja kopieras, sedan den kopierade formen vänder sig för att reproducera den i dörrlintel eller fönster.

Elliptisk båge

En båge är elliptisk om kurvan som ansluter två punkter är en sträcka eller sträcka av ellips. Ellipsen definieras som den geometriska platsen för de punkter vars avstånd till två punkter som ges alltid tillför en konstant mängd.

Ellipse är en kurva som förekommer i naturen: det är kurvan för planetens bana runt solen, som Johannes Kepler demonstrerade 1609.

I praktiken kan en ellips dras genom att sätta två stag på golvet eller två stift på papper och binda ett rep till dem. Då är repet spänt med markören eller pennan och kurvan ritas. En bit av ellips är en elliptisk båge. Följande animation illustrerar hur ellipsen dras:

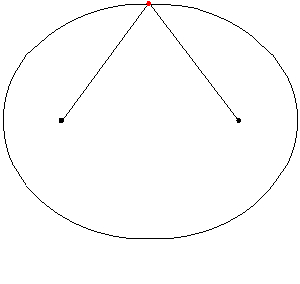Figur 5. Posen av en ellips med ett spänt rep. Källa: Wikimedia Commons

Figur 6 visar en elliptisk båge som ansluter punkter g och h.

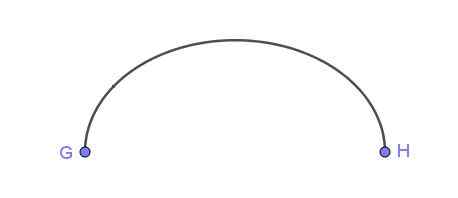Figur 6. Elliptisk båge som ansluter två poäng. Förberedd av Ricardo Pérez.

Exempel på bågar

Följande exempel hänvisar till hur man beräknar omkretsen av vissa specifika bågar.

Kan tjäna dig: transcendenta nummer: vad är, formler, exempel, övningar

Exempel 1

Figur 7 visar ett fönster som slutade i klippt cirkulärt båge. De dimensioner som visas i figuren är på fötterna. Beräkna båglängden.

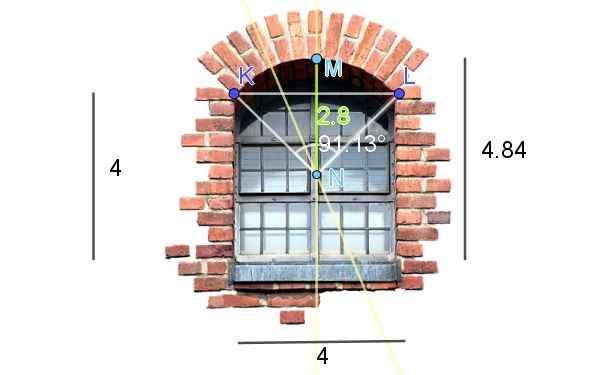Figur 7. Beräkning av fönsterens cirkulära båglängd. (Egna kommentarer - fönsterbild i Pixabay)

För att få mitten och radien för den cirkulära bågen i fönstret i fönstret görs följande konstruktioner på bilden:

-KL -segmentet ritas och dess mediatrix ritas.

-Då finns den högsta punkten för Lintel, som vi kallar m. KM -segmentet övervägs sedan och dess mediatrix dras.

Avlyssningen av de två mediarerna är punkt n och är också mitten av den cirkulära bågen.

-Nu måste du mäta längden på NM -segmentet, som sammanfaller med radien R för cirkulärbågen: r = 2.8 fot.

-Att veta längden på bågen utöver radien, vinkeln som bildar bågen. Som kan bestämmas med två metoder, eller mäts med en transportör eller beräknas växelvis med trigonometri.

I det visade fallet är vinkeln som bildar bågen 91,13º, som måste omvandlas till radianer:

 91,13º = 91,13º * π / 180º = 1,59 radianer

Vi beräknar äntligen längden s av bågen genom formeln S = α r.

S = 1,59 * 2.8 fot = 4,45 fot

Exempel 2

Hitta längden på den elliptiska bågen som visas i figur 8, känd r och den mindre semi -axeln s av ellipsen.

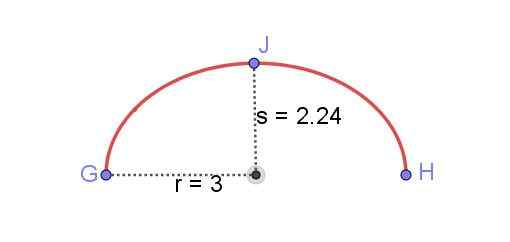Figur 8. Elliptisk båge mellan GH. Förberedd av Ricardo Pérez.

Att hitta längden på en ellips var under lång tid ett av de svåraste problemen med matematik. Lösningar uttryckta av elliptiska integraler kan erhållas men för att ha ett numeriskt värde måste dessa integraler i kraftserier utvidgas. Ett exakt resultat skulle kräva oändliga termer i dessa serier.

Lyckligtvis hittade det matematiska geniet av hinduiska ursprung Ramanujan, som levde mellan 1887 och 1920, en formel som ungefärligt ungefärligt omkretsen av en ellips:

Omkrets av en ellips = π [3 (r + s) - √ ((3r + s) (r + 3s))]]

Omkretsen av en ellips med r = 3 cm och s = 2.24 cm är 16,55 cm. Den elliptiska bågen har emellertid hälften av det värdet:

Elliptisk båglängd gh = 8.28 cm.

Referenser

1. Clemens S. 2008. Geometri och trigonometri. Pearson Education.
2. Garcia f. Numeriska förfaranden i Java. Ellipsens längd. Hämtad från: SC.Ehu.är
3. Dynamisk geometri. Bågar. Återhämtat sig från geometriadinamica.är
4. Pise. Ellipser och liknelser runt oss. Hämtad från: Pisedas.com
5. Wikipedia. Båge (geometri). Återhämtat sig från: det är.Wikipedia.com