Balansering av kemiska ekvationer

Vad är balanseringen av kemiska ekvationer?

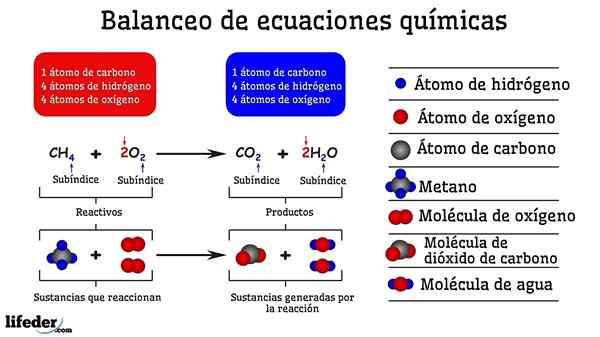
Balanseringen av kemiska ekvationer är en matematisk operation som genomförs för att upprätthålla lagen om bevarande av materia i reaktioner. Matter skapas eller förstörs inte. Därför måste antalet atomer före och efter en kemisk reaktion vara detsamma, både i reagensen och i produkterna.

För att balansera en kemisk ekvation måste du räkna atomerna före och efter pilen. Om siffrorna sammanfaller betyder det att reaktionen är balanserad. Annars kommer det att vara nödvändigt att matcha dessa siffror genom att modifiera de stökiometriska koefficienterna genom försök och fel, detta är den enklaste och mest intuitiva metoden för balans.

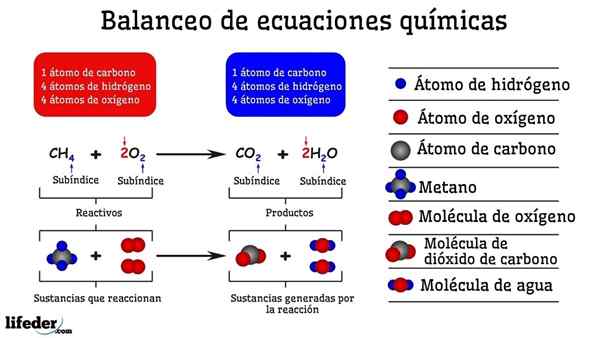Exempel på kemisk balansering av reaktionen mellan metan och två syremolekyler

När det är balanserat av försök och fel är det som om de togs bort eller tillsattes atomer på en av de två sidorna av Subbaja. Tills Subbaja inte är suspenderat horisontellt kommer den kemiska ekvationen inte att vara helt balanserad. Det kan inte finnas fler (skapa materia) eller mindre atomer (förstöra materia) på några sidor.

Enkla balanseringsexempel på ekvationer

I följande exempel ser du balanserade eller enkla att balansera kemiska ekvationer. Alla måste ha gemensamt att antalet atomer, för vart och ett av elementen, kommer att vara detsamma före och efter pilen när den kemiska ekvationen har balanserats.

Kvicksilveroxidation

2Hg +O₂  → Hg₂ANTINGEN₂

Vi har två element: kvicksilver (Hg) och syre (O). Vi uttrycker antalet atomer före (reagens) och sedan (produkter) på pilen:

Hg: 2 (vänster) - 2 (höger)

Det kan tjäna dig: Molarfraktion: Hur det beräknas, exempel, övningar

O: 2 (vänster) - 2 (höger)

Ekvationen är balanserad eftersom Hg -atomer och eller är desamma på båda sidor av pilen.

Väteförbränning

H₂ + ANTINGEN₂  → H₂ANTINGEN

Vi har två element igen: väte (H) och syre (O). Upprepa föregående steg:

H: 2 - 2

O: 2 - 1

På vänster sida finns ett syre mer än till höger. Vi måste därför lägga till ytterligare ett rätt syre. För att göra detta modifierar vi de stökiometriska koefficienterna, som är siffrorna som följer med och föregår formlerna. Om vi ​​placerar en 2 framför H₂Eller kommer att ge oss:

H₂ + ANTINGEN₂  → 2h₂ANTINGEN

H: 2 - 4

O: 2 - 2

Syre är balanserade. Men inte hydrogener. Du måste lägga till två hydrogener nu till vänster:

2h₂ + ANTINGEN₂ → 2h₂ANTINGEN

H: 4 - 4

O: 2 - 2

Och ekvationen är äntligen balanserad: samma antal H och eller före och efter pilen.

Observera att stökiometriska koefficienter (2 för h₂ och 1 för O₂) multiplicera abonnemangen på formlerna. Denna multiplikation ger oss det totala antalet atomer för ett specifikt element.

Magnesiumreduktion

Mg (nej₃)₂  +  2li → mg +2lino₃

Vi utvärderar atomnummer för varje element:

Mg: 1 - 1

Li: 2 - 2

N: 2 - 2

O: 6 - 6

Den kemiska ekvationen är redan balanserad och det finns inget behov av att balansera den.

Löst övningar

Innan du fortsätter att balansera någon ekvation är det alltid nödvändigt att bekräfta om den inte längre är balanserad. Som sagt, vi fortsätter med följande övning:

Övning 1

Balanserad eller inte?

Tro₂ANTINGEN₃ + H₂O → Tro (OH)₃

Vi har tre element: järn (tro), väte och syre. Ett förslag vid tidpunkten för balansekvationer är att börja räkna atomnumren för det mindre rikliga elementet i ekvationen; som vanligtvis skiljer sig från H och O. Således räknar vi först troens atomer:

Det kan tjäna dig: metylsalicylat

Tro: 2 - 1

Prenumeration 3 på (OH)₃ Multiplicera inte tron ​​till vänster. För H och O har vi:

H: 2 - 3

O: 4 - 3

Alla element är obalanserade.

Svängande

Innan ens balans H och O, måste vi balansera troens atomer: det minst rikliga elementet, eftersom det knappast finns 3 tro, till skillnad från 5 timmar och 7 eller 7 eller 7. Du måste då lägga till en tro till höger:

Tro: 2 - 2

Vad är lika med att sätta en 2 som stökiometrisk koefficient framför tron ​​(OH)₃. Ekvationen kommer att kvarstå:

Tro₂ANTINGEN₃ + H₂O → 2FE (OH)₃

Tro: 2 - 2

H: 2 - 6

O: 4 - 6

Men h och o eller fortsätta obalanserad. En h₂Eller bidra med 2 timmar och vi saknar 4 timmar. Därför kommer vi att lägga till ytterligare två timmar₂Eller för att vi ska ha tre timmar₂ANTINGEN:

Tro₂ANTINGEN₃ + 3 timmar₂O → 2FE (OH)₃

Och vi utvärderar igen:

Tro: 2 - 2

H: 6 - 6

O: 6 - 6

Lägg märke till hur de balanserade dem när vi en gång balanserade H. Ekvationen är äntligen balanserad.

Övning 2

Balanserad eller inte?

Ch₄  +  ANTINGEN₂  → CO₂  +  H₂ANTINGEN

Vi utvärderar antalet atomer för alla nuvarande element:

C: 1 - 1

H: 4 - 2

O: 2 - 3

Kol är balanserat, men detsamma händer inte med väte och syre. Ekvationen är obalanserad.

Svängande

Eftersom C är balanserad vill vi inte modifiera de stökiometriska koefficienterna för CH₄ eller co₂. Åtminstone inte i princip.

Vi fokuserar vår uppmärksamhet på H och O, särskilt på H. Därför att? Eftersom man ser ekvationen är det lättare att balansera H före eller. Vi måste lägga till 2 timmar till höger och placera en koefficient 2 framför H₂ANTINGEN:

Ch₄  +  ANTINGEN₂  → CO₂  +  2h₂ANTINGEN

C: 1 - 1

H: 4 - 4

O: 2 - 4

C och H är balanserade. Vi är kvar 2 eller kvar. Om var och en₂ bidrar med 2 eller kommer vi att lägga till en eller₂ extra så att de är 4 eller till vänster. Detta är detsamma som att placera en koefficient 2 framför O₂:

Kan tjäna dig: svaveloxid

Ch₄  +  2₂  → CO₂  +  2h₂ANTINGEN

C: 1 - 1

H: 4 - 4

O: 4 - 4

Och ekvationen är äntligen balanserad.

Övning 3

Balanserad eller inte?

N₂ + H₂  → NH₃

Vi utvärderar för våra två element n och h:

N: 2 - 1

H: 2 - 3

Ekvationen är inte balanserad.

Svängande

Vi börjar balansera n, elementet skiljer sig från h. Vi saknar en rättighet, och som alla NH₃ bidrar med 1 n, vi måste lägga till en annan NH₃ Att ha 2 n:

N₂ + H₂  → 2NH₃

N: 2 - 2

H: 2 - 6

Och nu saknar vi vänster. Om varje h₂ Bidra med 2 timmar till ekvationen, då måste vi lägga till ytterligare två så att det finns 6 timmar. Detta är detsamma som att placera en stökiometrisk koefficient 3 framför H₂:

N₂ + 3 timmar₂  → 2NH₃

N: 2 - 2

H: 6 - 6

Och den kemiska ekvationen är äntligen balanserad.

Referenser

1. Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning.
2. Kemi librettexts. (23 november 2020). Hur man skriver balanserade kemiska ekvationer. Återhämtad från: kem.Librettexts.org
3. Wikipedia. (2020). Kemisk ekvation. Hämtad från: i.Wikipedia.org
4. Principer för kemi. (s.F.). Skriva och balansera kemiska ekvationer. [Pdf]. Hämtad från: webben.Ung.Edu
5. Phet. (s.F.). Balansering av kemiska ekvationer. Återhämtad från: phet.Colorado.Edu
6. Armando Marín b. (s.F.). Allmän kemi: Balansering av ekvationer. [Pdf]. Återhämtat sig från: depa.Fquim.Unk.mx