Gratis konceptkoncept, ekvationer, övningar löst

De fritt fall Det är den vertikala rörelsen som ett objekt upplever när det tappas från en viss höjd nära jordens yta. Det är en av de enklaste och mest omedelbara rörelserna som är kända: i en rak linje och med konstant acceleration.

Alla föremål som tappas, eller som kastas vertikalt upp eller ner, rör dig med accelerationen 9.8 m/s² tillhandahålls av jordens svårighetsgrad, oavsett massa.

Fritt fall från en klippa. Källa: Pexels.com.

Detta faktum kan accepteras idag utan problem. Att förstå den verkliga naturen i det fria fallet tog dock ett tag. Grekerna hade redan beskrivit det och tolkat mycket i princip mot det fjärde århundradet a c.

[TOC]

Ekvationer av den fria fallrörelsen

En gång övertygad om att acceleration är densamma för alla kroppar som släpps under tyngdkraften är det dags att fastställa nödvändiga ekvationer för att förklara denna rörelse.

Det är viktigt att betona att luftmotstånd inte beaktas i denna första rörelsemodell. Resultaten av denna modell är dock mycket exakta och nära verkligheten.

I allt som följer kommer partikelmodellen att antas, det vill säga objektets dimensioner beaktas inte, förutsatt att hela massan är koncentrerad i en enda punkt.

För en jämnt accelererad rätlinjig rörelse tas den som en referensaxel och. Den positiva känslan tas upp och den negativa ner.

De kinematiska storleken

På detta sätt är ekvationerna i positionen, hastigheten och accelerationen beroende på tiden:

Acceleration

A = g = -9.8 m/s² (-32 fot/s²)

Position beroende på tid: och t)

y = y_antingen + v_antingen . T + ½ gt²

Var och_antingen Det är den ursprungliga positionen för mobilen och v_antingen är den första hastigheten. Kom ihåg att i den vertikala lanseringen är den initiala hastigheten nödvändigtvis annorlunda än 0.

Som kan skrivas som:

och och_antingen = v_antingen . T + ½ gt²

Δy = v_antingen . T + ½ gt²

Med 5och Att vara förskjutningen av mobilpartikeln. I enheter i det internationella systemet ges både positionen och förskjutningen i meter (m).

Hastighet beroende på tid: V (t)

v = v_antingen + g . t

Hastighet beroende på förskjutning

Det är möjligt att härleda en ekvation som kopplar förskjutning med hastighet, utan att ingripa tid. För att göra detta rensas tiden för den sista ekvationen:

Kan tjäna dig: kvantmekanisk modell av atomen

 Och det ersätts i förskjutningsekvationen:

Δy = v_antingen . T + ½ gt²

Torget är utvecklat med hjälp av den anmärkningsvärda produkten och termer omgrupperas.

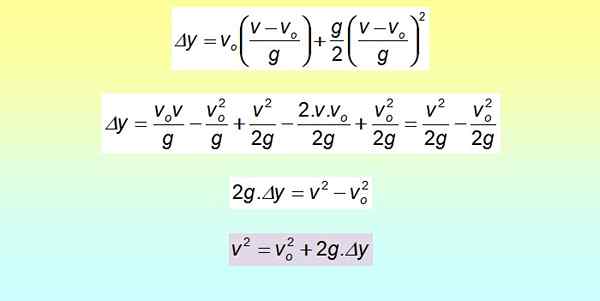
Denna ekvation är användbar när tiden inte är tillgänglig, men istället finns det hastigheter och förskjutningar, vilket framgår.

Exempel på fritt fall

Den uppmärksamma läsaren kommer att ha märkt närvaron av den initiala hastigheten v_antingen. De tidigare ekvationerna är giltiga för vertikala rörelser under tyngdkraften, både när objektet faller från en viss höjd, som om den kastas vertikalt upp eller ner.

När objektet sjunker är det helt enkelt gjort v_antingen = 0 och ekvationerna förenklas enligt följande.

Acceleration

A = g = -9.8 m/s² (-32 fot/s²)

Position beroende på tid: och t)

y = y_antingen+ ½ gt²

Hastighet beroende på tid: V (t)

v = g . t

Hastighet beroende på förskjutning

v² = 2g. Dy

Dy Det kommer också att vara negativt, sedan v² Det måste vara ett positivt belopp. Detta kommer att hända båda om ursprung antingen noll av koordinatsystemet vid startpunkten eller på marken.

Om läsaren föredrar det kan det ta riktningen nedåt som positiv. Tyngdkraften fortsätter att agera om man tror att det är + 9.8 m/s². Men du måste vara förenlig med den valda teckens konvention.

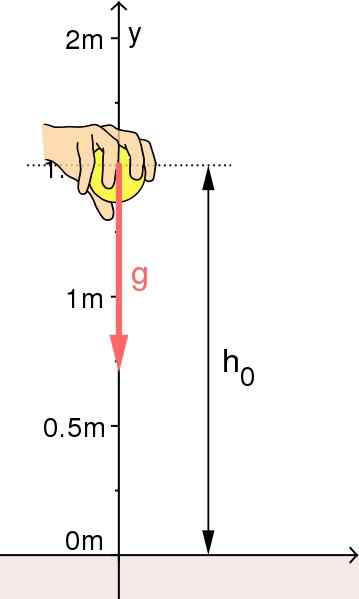Fri fall av ett objekt: Referenssystemets ursprung har valts på marken. Källa: Källa: Mikerun [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenser/BY-SA/4.0)]

Vertikal lansering

Här, naturligtvis, kan den initiala hastigheten inte vara noll. Vi måste tillhandahålla objektet för en impuls att gå upp. Enligt den initiala hastigheten kommer objektet att stiga till större eller mindre höjd.

Naturligtvis kommer det att finnas ett ögonblick där objektet tillfälligt stannar. Då har den maximala höjden uppnåtts med avseende på startpunkten. Även accelerationen är fortfarande G down. Låt oss se vad som händer i det här fallet.

Beräkning av den maximala höjden som uppnåtts

Att välja mig = 0:

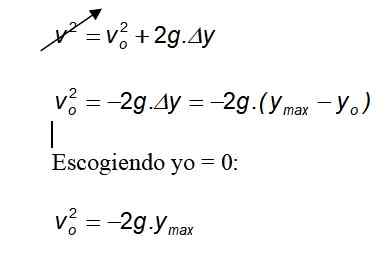
Eftersom tyngdkraften alltid pekar på marken i negativ riktning avbryts det negativa tecknet.

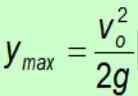
Maximal tidsberäkning

En liknande procedur tjänar till att hitta den tid det tar för objektet att nå den maximala höjden.

v = v_antingen + g . t

Det gör det v = 0

v_antingen = - g . t_Max

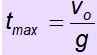
Flygtid är tiden som objektet varar i luften. Om objektet återgår till utgångspunkten är stigningstiden lika med nedstigningstiden. Därför är flygtid 2. T max.

Kan tjäna dig: Mikroskopisk skala: Egenskaper, grevepartiklar, exempel

Är två gånger T_Max Den totala tiden som objektet varar i luften? Ja, så länge objektet startar från en punkt och återvänder till det.

Om lanseringen är gjord av en viss höjd på marken och objektet får fortsätta till detta kommer flygtiden inte längre att vara dubbelt så mycket som den maximala tiden.

Löst övningar

I upplösningen av de övningar som följer kommer följande att övervägas:

1-höjden varifrån objektet tappas är liten jämfört med jordens radie.

2-luftmotståndet är föraktligt.

3-värdet på tyngdkraften är 9.8 m/s²

4-när det är problem med en enda mobil, helst väljs den och_antingen = 0 vid startpunkten. Detta underlättar vanligtvis beräkningar.

5-på mindre än det motsatta indikeras, tas uppåtriktningen som positiv.

6 -I de stigande och fallande kombinerade rörelserna erbjuder ekvationerna som tillämpas direkt rätt resultat, så länge konsistensen upprätthålls med tecknen: upp positivt, ner negativa och svårighetsgrad -9 -9.8 m/s² eller -10 m/s² Om du föredrar att runda (för mer komfort när du beräknar).

Övning 1

En boll kastas vertikalt upp med en hastighet på 25.0 m/s. Svara på följande frågor:

a) Hur mycket stiger det?

b) hur lång tid tar det att uppnå sin högsta punkt?

c) Hur lång tid tar bollen att röra vid jordens yta efter att den uppnår sin högsta punkt?

d) Vad är din hastighet när du återvänder till nivån där den började?

Lösning

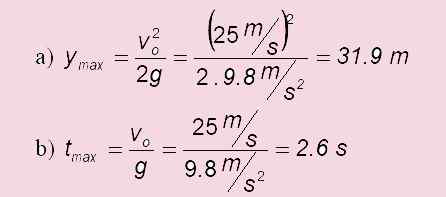
c) Vid en nivåstart: t_flyg = 2 . t_Max = 2 x6 s = 5.1 s

d) När den återgår till startpunkten har hastigheten samma storlek som den initiala hastigheten men motsatt riktning, därför måste den vara - 25 m/s. Det kontrolleras enkelt genom att ersätta värden i ekvationen för hastighet:

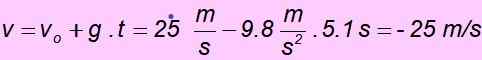
Övning 2

En liten postväska släpps från en helikopter som är fallande med en konstant hastighet på 1.50 m/s. Efter 2.00 S Beräkna:

a) Vad är resväskans hastighet?

b) Hur långt är resväskan under helikoptern?

c) Vilka är dina svar för avsnitt a) och b) Om helikoptern stiger med konstant hastighet på 1.50 m/s?

Lösning

Sektion A

När resväskan överger helikoptern bär därför den ursprungliga hastigheten på den, därför v_antingen = -1.50 m/s. Med den angivna tiden har hastigheten ökat tack vare tyngdkraften:

Kan tjäna dig: himmelkroppar

v = v_antingen + g . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Avsnitt B

Låt oss se hur mycket resväskan har kommit ner med avseende på utgångspunkten vid den tiden:

Resväska: Dy = v_antingen . T + ½ gt² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Det har valts och_antingen = 0 Vid startpunkten, som anges i början av avsnittet. Det negativa tecknet indikerar att resväskan har fallit ner 22. 6 m under utgångspunkten.

Under tiden helikoptern Det har fallit snabbt -1.50 m/s, antar vi ständigt, därför har helikoptern på den angivna tiden på 2 sekunder rest:

Helikopter: Δy = v_antingen.t = -1.femtio x 2 m = -3 m.

Därför separeras resväska och helikopter efter 2 sekunder med ett avstånd från:

D =| -22.6 - (-3) | M = 19. 6 m.

Avståndet är alltid positivt. För att lyfta fram detta faktum används det absoluta värdet.

Avsnitt C

När helikoptern stiger har den en hastighet på + 1.5 m/s. Med den hastigheten kommer resväskan ut, så att efter 2 s redan bär:

v = v_antingen + g . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

Hastigheten visar sig vara negativ, eftersom resväskan efter 2 sekunder rör sig. Har ökat tack vare tyngdkraften, men inte så mycket som i avsnitt a.

Nu hittar vi hur mycket resväskan har kommit ner med avseende på utgångspunkten under de första 2 sekunderna av resan:

Valija: Δy = v_antingen . T + ½ gt² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Under tiden helikoptern Det har stigit När det gäller utgångspunkten och har gjort det med konstant hastighet:

Helikopter: Δy = v_antingen.T = +1.femtio x 2 m = +3 m.

Efter 2 sekunder separeras resväska och helikopter med ett avstånd från:

D =| -16.6 - (+3) | M = 19.6 m

Avståndet som skiljer dem är detsamma i båda fallen. Resväskan reser mindre vertikalt avstånd i det andra fallet, eftersom dess initiala hastighet riktades uppåt.

https: // youtu.vara/w2UVETXWSFK

Referenser

1. Kirkpatrick, l. 2007. Fysik: En titt på världen. 6^ta Förkortad upplaga. Cengage Learning.  23 - 27.
2. Rex, a. 2011. Fysikens grunder. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14^th. Ed. Volym 1. 50 - 53.
4. Serway, R., Vule, c. 2011. Fysikens grunder. 9^na Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fysik 10. Pearson Education. 133 - 149.