Känsligt värmekoncept, formler och övningar löst

han Känslig värme Det är den termiska energin som levereras till ett objekt som får dess temperatur att öka. Det är motsatsen till latent värme, där termisk energi inte ökar temperaturen utan främjar en fasförändring, till exempel från fast till vätska.

Ett exempel klargör konceptet. Anta att vi har en kruka med vattentemperaturen på 20 ° C. När vi placerar det i hornet ökar den tillförsel som levereras långsamt till vattenstemperaturen till 100 ° C (kokningstemperatur på vattnet vid havsnivån). Den levererade värmen kallas känslig värme.

Värmen som värmer dina händer är känslig värme. Källa: Pixabay

När vattnet når kokningstemperaturen ökar inte värmen som levereras av hornillaen längre vattentemperaturen, som kvarstår vid 100 ° C.  I detta fall investeras den levererade termiska energin i förångning av vatten. Den levererade värmen är latent eftersom den inte höjde temperaturen utan orsakade en förändring av vätskefasen till gasfasen.

Det är ett experimentellt faktum att den känsliga värmen som krävs för att uppnå en viss temperaturvariation är direkt proportionell mot den variationen och objektets massa.

[TOC]

Koncept och formler

Det har observerats att förutom massa och temperaturskillnad beror känslig värme också på materialet. Av denna anledning kallas proportionalitetskonstanten mellan den känsliga värmen och produktens produkt genom temperaturskillnaden den specifika värmen.

Mängden levererad känslig värme beror också på hur processen genomförs. Till exempel är det annorlunda om processen utförs med konstant volym än konstant tryck.

Formeln för känslig värme i en process isobarisk, Det vill säga konstant tryck, det är som följer:

Q = CP . m (tF - TYo)

I föregående ekvation Q Det är den känsliga värmen som levereras till massobjektet m, som har höjt sin ursprungliga temperatur T_Yo Fram till det slutliga värdet Tf. I föregående ekvation visas det också cp, vilket är materialets specifika värme vid konstant tryck eftersom processen har genomförts på detta sätt.

Observera att känslig värme är positiv när den absorberas av objektet och orsakar en temperaturökning.

I det fall en gas som är innesluten i en styv behållare levereras kommer processen att vara isokorisk, det vill säga i konstant volym; Och den känsliga värmeformeln kommer att skrivas så här:

Kan tjäna dig: böljande rörelse: egenskaper, typer av vågor, exempel

Q = cv. m . (TF - TYo)

Den adiabatiska koefficienten γ

Förhållandet mellan den specifika värmen vid konstant tryck och den specifika värmen vid konstant volym för samma material eller ämne kallas Adiabatisk koefficient, som vanligtvis betecknas med Gamma Gamma y -bokstaven.

han Adiabatisk koefficient är större än enheten. Den värme som krävs för att höja temperaturen på en kropp av ett gram massa till en klass är större i en isobarisk process än i en isokorisk.

Detta beror på att i det första fallet av värmen används för att göra mekaniskt arbete.

Förutom den specifika värmen definieras vanligtvis värmekapaciteten. Detta är mängden värme som krävs för att höja temperaturen på den kroppen en centigrerad examen.

Värmekapacitet c

Värmekapacitet betecknas med C versaler, medan den specifika värmen med c små bokstäver. Förhållandet mellan båda beloppen är:

C = c⋅ m

Var m Det är kroppens massa.

Molarspecifik värme används också, vilket definieras som mängden känslig värme som krävs för att höja till en Celsius eller Kelvin -temperatur.

Specifik värme i fasta ämnen, vätskor och gaser

Den specifika molära värmen för de flesta fasta ämnen har ett värde nära 3 Times R, var R Det är den universella konstanten av gaser. R = 8.314472 J/(mol ℃).

Till exempel har aluminium specifik molvärme 24.2 J/(mol ℃), Koppar 24.5 J/(mol ℃), guld 25.4 J/(mol ℃), och söt järn 25.1 J/(mol ℃). Observera att dessa värden är nära 3R = 24,9 J/(mol ℃).

Å andra sidan, för de flesta gaser är den specifika värmen nära N (r/2), var är n ett heltal och R Det är den universella konstanten av gaser. Heltalet n är relaterat till antalet grader av molekylens frihet som bildar gasen.

Till exempel, i en idealisk monoatomisk gas, vars molekyl bara har de tre frihetsgraderna, är den specifika molvärmen till konstant volym 3 (R/2). Men om det är en idealisk diatomisk gas är två rotationsgrader dessutom, så cv = 5 (R/2).

Kan tjäna dig: Semicircle: Hur man beräknar omkretsen, området, centroid, övningar

I de ideala gaserna uppfylls följande samband mellan den specifika värmemolvärmen och konstant volym: cp = cv + R.

Sidan omnämnande förtjänar vatten. I flytande tillstånd vid 25 ℃ vatten har cp = 4 1813 J/(g ℃), Vattenånga vid 100 grader har Celsius cp = 2 080 J/(g ℃) Och vattenis till nollklass Celsius har cp = 2 050 J/(g ℃).

Skillnad med latent värme

Matter finns i tre stater: fast, flytande och gasformigt. För att förändra tillståndet krävs energi, men varje substans svarar på det på ett annat sätt enligt dess molekylära och atomegenskaper.

När en fast smälter eller en vätska förångas förblir objektets temperatur konstant tills alla partiklar har ändrat sin status.

Därför är det möjligt att ett ämne samtidigt är i jämvikt i två faser: fast - vätska eller vätska - ånga, till exempel. En mängd av ämnet kan passera från ett tillstånd till ett annat genom att lägga till eller ta bort lite värme, medan temperaturen förblir fixerad.

Värmen som levereras till ett material får sina partiklar att vibrera snabbare och öka dess kinetiska energi. Detta innebär en temperaturökning.

Det är möjligt att energin de förvärvar är så stor att de inte längre återvänder till sin jämviktsposition och ökar separationen mellan dem. När detta händer ökar temperaturen inte, men ämnet passerar från fast till vätska eller gasvätska.

I den värme som krävs för att detta ska hända är det känt som latent värme. Därför är latent värme värme genom vilken ett ämne kan ändra fas.

Här är skillnaden med känslig värme. Ett ämne som absorberar känslig värme ökar temperaturen och förblir i samma tillstånd.

Hur man beräknar latent värme?

Den latenta värmen beräknas genom ekvation:

Q = m . L

Var L Det kan vara den specifika värmen för förångning eller fusion. Enheterna av L De är energi/massa.

Forskare har gett många värme valörer, beroende på vilken typ av reaktion som han deltar. Således finns det till exempel reaktionsvärmen, värmen av förbränning, värme av stelning, lösningsvärmen, sublimeringsvärmen och många andra.

Kan tjäna dig: Kinetisk energi: Egenskaper, typer, exempel, övningar

Värdena för många av dessa värmtyper för olika ämnen är tabellerade.

Löst övningar

Exempel 1

Anta en som har en 3 kg massaluminium. Ursprungligen är det vid 20 ° C och du vill höja temperaturen upp till 100 ° C. Beräkna den nödvändiga känsliga värmen.

Lösning

Först måste vi veta den specifika värmen i aluminium

cp = 0,897 J / (g ° C)

Så mängden värme som behövs för att värma aluminiumstycket kommer att vara

Q = cp m (tf - ti) = 0,897 * 3000 * (100 - 20) j

Q = 215280 J

Exempel 2

Beräkna mängden värme som behövs för att värma 1 liter vatten från 25 ° C till 100 ° C vid havsnivån. Uttrycka resultatet också i kilokalorier.

Lösning

Det första vi bör komma ihåg är att 1 liter vatten väger 1 kg, det vill säga 1000 gram.

Q = cp m (tf - ti) = 4,1813 j/(g ℃) * 1000 g * (100 ℃ - 25 ℃) = 313597,5 j

Kalorier är en energifon som definieras som den känsliga värmen som krävs för att höja ett gram vatten till en Celsius. Därför motsvarar 1 kalori 4 1813 joules.

Q = 313597.5 J * (1 kal / 4 1813 J) = 75000 lime = 75 kcal.

Exempel 3

En bit av 360,16 gram material upphettas från 37 ℃ till 140 ℃. Den levererade termiska energin är 1150 kalorier.

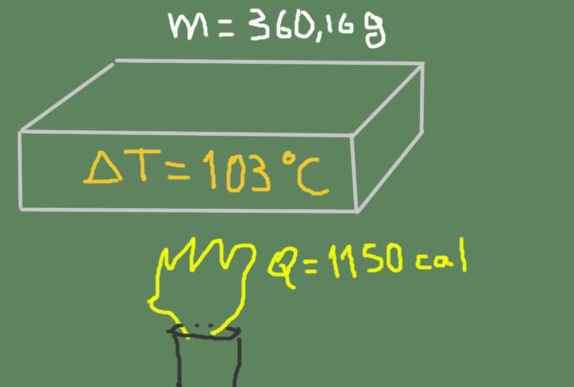Uppvärmning av provet. Källa: Självgjord.

Hitta materialets specifika värme.

Lösning

Vi kan skriva den specifika värmen baserad på känslig värme, massa och temperaturvariation enligt formeln:

cp = Q /(m Δt)  

Byt ut de uppgifter vi har följande:

cp = 1150 kal / (360,16 g * (140 ℃ - 37 ℃)) = 0.0310 CAL / (G ℃)

Men eftersom en kalori motsvarar 4 1813 J, kan resultatet också uttryckas som

cp = 0,130 J / (g ℃)

Referenser

1. Giancoli, D.  2006. Fysik: Principer med applikationer. 6^th. Ed. Prentice hall. 400 - 410.
2. Kirkpatrick, l. 2007. Fysik: En titt på världen. 6^ta Förkortad upplaga. Cengage Learning. 156 - 164.
3. Tippens, s. 2011. Fysik: koncept och applikationer. 7th. Reviderad upplaga. McGraw Hill. 350 - 368.
4. Rex, a. 2011. Fysikens grunder. Pearson. 309 - 332.
5. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14^th. Volym 1. 556 - 553.
6. Serway, R., Vule, c. 2011. Fysikens grunder. 9^na Cengage Learning. 362 - 374.