Kapacitansenheter, formler, beräkning, exempel

De Kapacitans Det är förhållandet mellan belastningen på en kondensator eller tränare, mätt i Coulomb, och dess elektriska potential eller spänning, mätt i volt. Det uttrycks i Faradio (F) -enheter, för att hedra Michael Faraday (1791-1867).

Kapacitans definieras också som egenskapen eller kapaciteten för en kondensator eller en uppsättning elektriska kondensatorer, som mäts med mängden elektrisk laddning som kan lagras, separat, per enhet för elektrisk potential.

Lamporna såväl som någon annan elektrisk enhet måste en del av sin drift till kapacitans. Källa: Pixabay.

Termen kapacitans introduceras som ett resultat av skapandet av en elektrisk anordning som kallas kondensatorn, uppfunnet av den preussiska forskaren Ewald Georg von Kleist, 1745, och oavsett den holländska fysikern Pieter van Musschenbroek.

Kondensatorer är elektriska enheter som lagrar elektrisk laddning och laddar ner den direkt. Den här egenskapen har använts i många elektriska enheter, till exempel tv, radio, lampor, dator, bland många andra i vardagen.

[TOC]

Kondensator och kapacitans

En kondensator eller kondensator består av två förare som har lika laster och på annat sätt. Förare kallas rustning rustning eller kondensatorplattor.

En plack är kopplad till den positiva (+) terminalen på ett batteri, medan den andra plattan är kopplad till det negativa (-). Eftersom plattorna har lika laster och det motsatta tecknet är nettobelastningen för en kondensator noll (0).

Kapacitans är förhållandet mellan belastningen på en förare eller ledare som bildar en kondensator och värdet på spänningsskillnaden mellan kondensorplattorna.

Kan tjäna dig: Rosario köldmedium

Enheter och formler

Kapacitansformeln är som följer:

C = q / v

Där C är kapacitans, q lasten (vars enhet är coulomb) och v  Spänningen (volt)

Kapacitansenheten är Faradio (F), vilket motsvarar Coulomb / Voltio. Faradio är en mycket stor enhet, så mikrofradium (µF) används, motsvarande 10^-6 farad; eller Faradio Peak (PF), vilket motsvarar 10^-12 farad.

Hur beräknas kapacitans?

Vad kommer att vara kapacitansvärdet för en kondensator vars plattor har en belastning på 5 · 10^-3 Coulomb och en 6 volt spänningsskillnad?

Tillämpa formeln vi löser:

C = q / v

= (5 · 10^-3 Coulomb) / (6 volt)

= 8,33 · 10^-4  farad

Exempel

Kapacitansformeln varierar beroende på typ av kondensator.

Parallella plattor kondensator

C = kε_antingenA / d

k är den dielektriska konstanten, som har ett värde på 1 i luften och tomrummet. Av denna anledning reduceras formeln till:

C = ε_antingenA / d

ε_antingen Det är den dielektriska konstanten, vars värde är nära 8 854 · 10^-12 F · m^-1, A är området eller ytan på de parallella plattorna uttryckta i m², medan d Avståndet som skiljer de parallella plattorna.

Sfärisk kondensator

C = 4πε_antingenR

Där r är sfärens radie i meter.

Koncentriska sfärer

C = 4πε_antingen / (1/ r₁ - 1/r₂)

Koncentrisk cylinderkondensator

C = 2πε_antingenl/ln (r₂ / R₁)

Var l är längden på koncentriska cylindrar i meter.

Löst övningar

Parallella platta plattor kondensator

Vad är kapaciteten för en kondensator eller kondensator i luften med ett område på sina 3 cm plattor² och separeras med ett avstånd av 2 mm?

Kan tjäna dig: 12 exempel på kemiska baser

Vi har formeln:

C = ε_antingenA/d

Och uppgifterna:

ε_antingen = 8 854 x 10^-12 F · m^-1

A = 3 cm² (3 · 10^-4 m²)

D = 2 mm (2 · 10^-3 m)

Fortsätt för att ersätta:

C = (8 854 · 10^-12 F · m^-1) (3 · 10^-4 m²) / (2 · 10^-3 m)

= 1,3281 · 10^-14 F

Kondensator eller sfärformad kondensator

Om jorden betraktas som en sfärisk kondensator med en radie (R) på 6.370 km: Vad blir värdet på din kapacitans?

Data:

C = 4πε_antingenR

Π = 3 1416

ε_antingen = 8 854 · 10^-12 F.m^-1

R = 6.370 km (6,37 · 10⁶ m)

Värdena i kapacitansformeln ersätts igen:

C = (4 · 3,1416) (8 854 · 10^-12 F · m^-1) (6.37 · 10⁶ m)

= 7,09 · 10^-8 F

= 709 µF

Kondensatorer

Kondensatorer eller kondensatorer kan kombineras i serie eller parallellt.

Seriekondensatorer

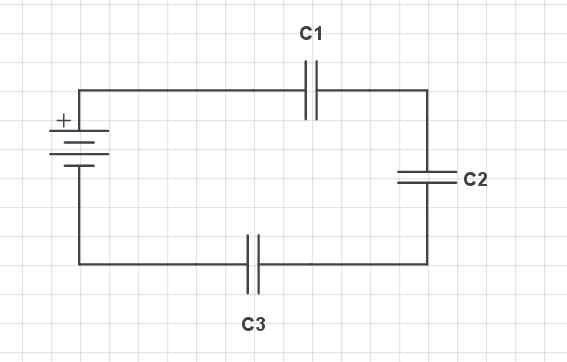Seriekondensatorer. Gabriel Bolívar Source via CircuitLab

Den övre bilden visar tre seriekondensatorer (c₁, C₂ och C₃), liksom ett batteri med sina positiva (+) och negativa (-) terminaler. Dessa kondensatorer har en serie egenskaper i förhållande till deras spänning, belastning och kapacitans.

Spänningsfall (ΔV) i kondensatorer

ΔV_t = ΔV₁   +   ΔV₂   +    ΔV₃

Den totala spänningsfallet i en uppsättning seriekondensatorer är lika med summan av spänningsfallen hos kondensatorerna.

Börda  av kondensatorer

Q_t = Q₁ = Q₂ = Q₃

Samma belastningsmängd cirkulerar genom serien.

Kondensatorer

Motsvarande kapacitans av seriekondensatorer presenterar följande förhållande:

1 c_eq  = 1/c₁  +   1 c₂   +   1 c₃

Parallellkondensatorer

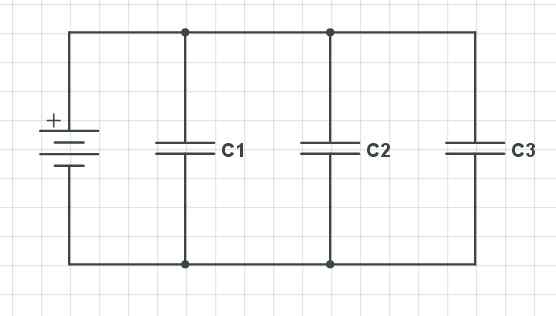Parallellkondensatorer. Gabriel Bolívar Source via CircuitLab.

Upp vi har tre kondensatorer ordnade parallellt (c₁, C₂ och C₃), som håller i förhållande till spänningsfallet, belastningen och kapacitansen följande beteende:

Kan tjäna dig: alkenes

Spänningsfall i kondensatorer

ΔV_t  = ΔV₁  = ΔV₂  = ΔV₃

I parallella kondensatorer är den totala spänningsfallet i kondensatorer densamma som den befintliga för var och en av kondensatorerna.

Kondensatorer

Q_t  = Q₁  +  Q₂  +  Q₃

I ett system parallellt är den totala belastningen av kondensatorerna lika med summan av belastningen för alla kondensatorer.

Kondensatorer

C_eq  = C₁  +  C₂   +  C₃

I ett parallellt system är motsvarande kapacitans av dem lika med summan av kapacitanserna för alla kondensatorer.

Exempel på en övning

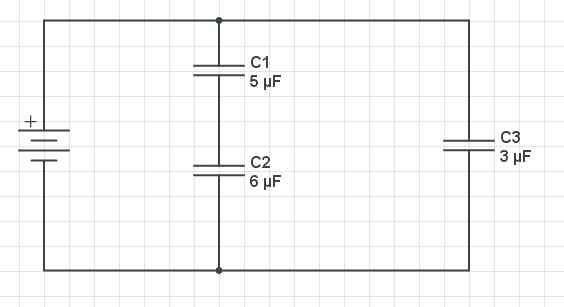Exempel på ett problem och parallella kondensatorproblem. Gabriel Bolívar Source via CircuitLab.

Ett schema med tre kondensatorer visas ovan: c₁ och C₂ De är ordnade i serie och de är parallellt med C₃. Kondensatorer Kapacitans är följande: c₁ = 5 µF, c₂ = 6 µF och c₃ = 3 uf. Hitta motsvarande kapacitans av kretsen.

Först är motsvarande kapacitans av c₁ och C₂ som är i serie.

1 c_Eq1,2 = 1/c₁  +  1 c₂

1 c_Eq1,2 = 1/5 µF +1/6 µF

1 c_Eq1,2 = (11/30) µF

C_Eq1,2 = 30 µF / 11

= 2,72 µF

Kondensatorer 1 och 2 är parallellt med C₃. Så motsvarande kapacitans av c₁, C₂ och C₃ är lika med c_Eq1,2 +  C₃.

C_Eq1,2,3 = 2,72 µF +3 µF

= 5,72 µF

Referenser

1. Serway, R. TILL. och Jewett, J. W. (2009). Fysik för vetenskap och teknik. Volym 2. Sjunde upplagan. Redaktionell cengage -lärande.
2. Reddick, R och Halliday, D. (1965). Fysisk.  Del 2. Andra upplagan på spanska. Kontinental redaktion.TILL.
3. Studie. (22 april 2015). Kapacitans: Enheter och formel. Återhämtat sig från: studie.com
4. Lumes fysik. (s.F.). Kondensatorer i serie och parallella. Återhämtat sig från: kurser.Lumenarning.com
5. Redaktörerna för Enyclopaedia Britannica. (2020). Kapacitans. Återhämtat sig från: Britannica.com