Enhetscellegenskaper, röd konstant och typer

De Enhetscell Det är ett imaginärt utrymme eller en region som representerar det minsta uttrycket för en helhet; Det i fallet med kemi skulle helheten vara en kristall som består av atomer, joner eller molekyler, som beställs efter ett strukturellt mönster.

I det dagliga livet kan du hitta exempel som förkroppsligar detta koncept. För detta är det nödvändigt att uppmärksamma objekt eller ytor som uppvisar en viss repetitiva ordningsordning. Vissa mosaiker, bas -relation, hantverk.

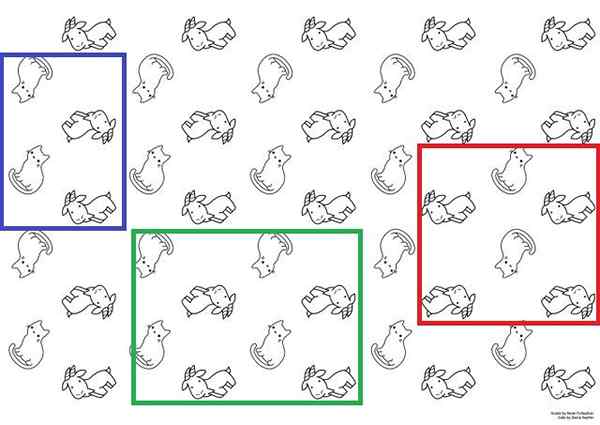Enhetsceller på katt- och getpapper. Källa: Hanna Petruschat (WMDE) [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenser/BY-SA/4.0)].

För att illustrera det tydligare har du den överlägsna bilden som kan användas som ett vävpapper. I den visas katter och getter med två alternativa sinnen; Katter är fötter eller huvud, och getterna ser upp eller ner.

Dessa katter och getter upprättar en repetitiv strukturell sekvens. För att bygga allt papper skulle det räcka för att reproducera den enhetliga cellen vid ytan ett tillräckligt antal gånger, med hjälp av translationella rörelser.

De möjliga enhetscellerna representeras med de blå, gröna och röda lådorna. Någon av dessa tre kan användas för att få papperet; Men det är nödvändigt att flytta dem fantasifullt längs ytan för att ta reda på om de reproducerar samma sekvens som observerats i bilden.

Från och med den röda rutan skulle det uppskattas att om tre kolumner (av katter och getter) flyttades till vänster, skulle två getter inte längre visas i sin nedre del utan bara en. Därför skulle det leda till en annan sekvens och kan inte betraktas som en enhetscell.

Medan om de fantasifullt flyttar de två lådorna, blå och gröna, skulle samma papperssekvens erhållas. Båda är enhetsceller; Den blå rutan följer dock definitionen mer, eftersom den är mindre än den gröna rutan.

[TOC]

Enhetscellegenskaper

Hans egen definition, utöver det nyligen förklarade exemplet, klargör flera av dess egenskaper:

-Om de rör sig i rymden, oavsett riktning, kommer det kompletta fasta eller glaset att erhållas. Detta beror på att, som nämnts med katter och getter, reproducerar den strukturella sekvensen; vilket är lika med den rumsliga fördelningen av repetitiva enheter.

-De måste vara så små som möjligt (eller ockupera liten volym) jämfört med andra möjliga cellalternativ.

Kan tjäna dig: metylmalonsyra: struktur, egenskaper, syntes, användningar

-De är, vanliga, symmetriska. På samma sätt återspeglas dess symmetri bokstavligen i förenings kristaller; Om enhetscellen i ett salt är kubiskt kommer dess kristaller att vara kubiska. Det finns emellertid kristallina strukturer som beskrivs med enhetsceller med förvrängda geometrier.

-De innehåller de repetitiva enheterna, som kan ersättas med punkter, som i tur och ordning tre -dimensionellt vad som kallas en retikel. I föregående exempel representerar katter och getter retikulära punkter, sett från ett högre plan; det vill säga två dimensioner.

Antal repetitiva enheter

De repetitiva enheterna eller retikulära punkter i enhetscellerna upprätthåller samma andel av de fasta partiklarna.

Om antalet katter och getter räknas inuti den blå rutan kommer det att finnas två katter och getter. Detsamma gäller för den gröna rutan, och med den röda rutan också (även om det redan är känt att det inte är en enhetscell).

Anta till exempel att katter och getter är atomer G respektive C (en konstig djursvetsning). Eftersom andelen mellan G och C är 2: 2 eller 1: 1 i den blå rutan kan det förväntas utan misstag att det fasta ämnet kommer att ha GC (eller CG) -formeln.

När det fasta ämnet har mer eller mindre kompakta strukturer, som med salter, metaller, oxider, sulfider och legeringar, finns det i enhetscellerna inga hela repetitiva enheter; Det vill säga, det finns delar eller delar av dem, som lägger till en eller två enheter.

Detta är inte fallet för GC. Om den blå rutan "skulle starta" till katter och getter i två (1/2G och 1/2C) eller fyra delar (1/4G och 1/4C). I nästa avsnitt kommer det att ses att i dessa enhetsceller är retikulära punkterna bekvämt uppdelade på detta och andra sätt.

Vilka nätverkskonstanter definierar en enhetscell?

De enhetliga cellerna i GC -exemplet är två -dimensionella; Detta gäller emellertid inte i de verkliga modellerna som överväger de tre dimensionerna. Således förvandlas lådorna eller parallellogrammen till parallellepípedos. Nu tar termen "cell" större förnuft.

Dimensionerna på dessa celler eller parallellepipeds beror på hur länge deras respektive sidor och vinklar är.

I den nedre bilden har du det nedre bakre hörnet av parallellpipen, sammansatt av sidorna till, b och c, och vinklarna α, ß och y.

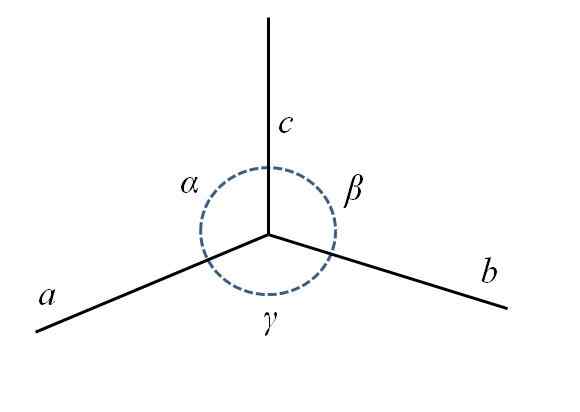Parametrar för en enhetscell. Källa: Gabriel Bolívar.

Som du kan se, till är lite längre än b och c. I mitten har du en cirkel med en prickad linje för att indikera vinklarna α, ß och y, mellan Växelström, CB och ba, respektive. För varje enhetscell har dessa parametrar konstanta värden och definierar deras symmetri och resten av glaset.

Kan tjäna dig: kalciumperoxid (CAO2): egenskaper, risker och användningar

Genom att tillämpa lite fantasi skulle bildparametrarna definiera en cell som liknar en sträckt kub i dess kant till. Således uppstår enhetsceller med olika längder och vinklar på dess kanter, som också kan klassificeras i olika typer.

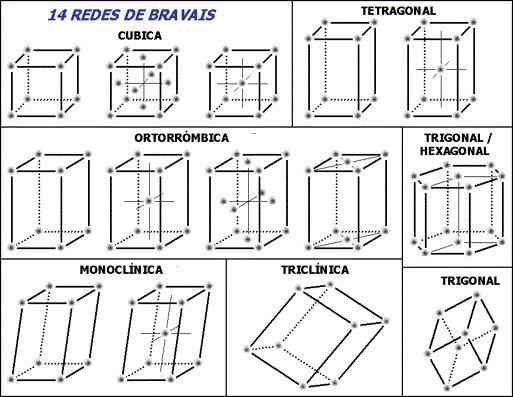
Grabbar

De 14 Bravais -nätverken och de sju grundläggande kristallina systemen. Källa: Den ursprungliga uppladdaren var Angrense på Portuguese Wikipedia. [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Obs! För att starta de streckade linjerna inuti enhetscellerna: de anger den nedre bakre vinkeln, som förklarats. Följande fråga kan ställas, var är retikulära punkter eller repetitiva enheter? Även om de ger fel intryck av att cellerna är tomma, ligger svaret i sina hörn.

Dessa celler genereras eller väljer på ett sådant sätt att de repetitiva enheterna i deras vertikaler finns (grå punkter på bilden). Beroende på värdena på de parametrar som fastställts i föregående avsnitt, konstant för varje enhetscell, härleds sju kristallina system.

Varje kristallint system har sin egen enhetliga cell; Den andra definierar den första. I den övre bilden finns sju lådor, motsvarande de sju kristallina systemen; eller lite mer sammanfattning, kristallina nätverk. Således motsvarar till exempel en kubisk enhetscell ett av de kristallina systemen som definierar ett kubiskt kristallint nätverk.

Enligt bilden är de kristallina systemen eller nätverk:

-Kubisk

-Tetragonal

-Ortorrombica

-Hexagonal

-Monoklinisk

-Triklinisk

-Trigonal

Och inom dessa kristallina system andra som utgör de fjorton näten av Bravais; att bland alla kristallina nätverk är de de mest grundläggande.

Kubisk

I en kub är alla dess sidor och vinklar desamma. Därför uppfylls följande i denna enhetscell:

till = b = c

α = β = y = 90º

Det finns tre kubiska enhetsceller: enkla eller primitiva, centrerade på kroppen (BCC) och centrerad på ansikten (FCC). Skillnaderna ligger i hur punkterna (atomer, joner eller molekyler) och i antalet av dem är fördelade.

Vilka av dessa celler är den mest kompakta? Den vars volym är mer ockuperad av punkter: kubiken centrerad på ansikten. Observera att om vi ersätter punkterna med katter och getter i början, skulle de inte begränsas till en enda cell; De skulle tillhöra och delas av flera. Återigen skulle det vara delar av G eller C.

Det kan tjäna dig: hydrokoloid

Antal enheter

Om katter eller getter var i topparna, skulle de delas av 8 enhetsceller; Det vill säga varje cell skulle ha 1/8 av g eller c. Tillsammans eller föreställ dig 8 kuber, i två kolumner med två rader vardera, för att visualisera det.

Om katter eller getter var på ansikten, skulle de endast delas av 2 enhetsceller. För att se det räcker det att samla två kuber.

Å andra sidan, om katten eller geten var i mitten av kuben, skulle de bara tillhöra en enda enhetlig cell; Detsamma händer med lådorna i huvudbilden, när konceptet adresserades.

Sa då ovanstående, inom en enkel kubikcell en Enhet eller retikulär punkt, eftersom den har 8 vertikaler (1/8 x 8 = 1). För kubikcellen centrerad i kroppen har du: 8 vertikaler, vilket är lika med en atom och en punkt eller enhet i mitten; Därför finns det två enheter.

Och för kubikcellen centrerade på ansikten du har: 8 vertikaler (1) och sex ansikten, där hälften av varje punkt eller enhet delas (1/2 x 6 = 3); Därför har det fyra enheter.

Tetragonal

Liknande kommentarer kan göras med avseende på den enhetliga cellen för det tetragonala systemet. Dess strukturella parametrar är följande:

till = b Sider c

α = β = y = 90º

Ortorrombica

Parametrarna för den ortorrombiska cellen är:

till Sider b Sider c

α = β = y = 90º

Monoklinisk

Parametrarna för monoklinisk cell är:

till Sider b Sider c

α = y = 90º; β ≠ 90º

Triklinisk

Parametrarna för den tricliniska cellen är:

till Sider b Sider c

α ≠ β ≠ γ ≠ 90º

Hexagonal

Parametrarna för den hexagonala cellen är:

till = b Sider c

α = β = 90º; γ ≠ 120º

Egentligen utgör cellen den tredje delen av ett hexagonalt prisma.

Trigonal

Och slutligen är parametrarna för trigonalcellen:

till = b = c

α = β = γ ≠ 90º

Referenser

1. Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning P 474-477.
2. Shiver & Atkins. (2008). Oorganisk kemi. (Fjärde upplagan). MC Graw Hill.
3. Wikipedia. (2019). Primitiv cell. Hämtad från: i.Wikipedia.org
4. Bryan Stephanie. (2019). Enhetscell: Latice -parametrar och kubiska strukturer. Studie. Återhämtat sig från: studie.com
5. Akademisk resurscenter. (s.F.). Kristallstrukturer. [Pdf]. Illinois Institute of Technology. Hämtad från: webben.jag det.Edu
6. Belford Robert. (7 februari 2019). Crystal Latices och enhetsceller. Kemi librettexts. Återhämtad från: kem.Librettexts.org