Tyngdpunktens centrum, beräkning, exempel

han tyngdkraftscentrum av en mätbar storlek kropp är punkten där dess vikt anses vara applicerad. Det är därför ett av de främsta begreppen statisk.

Det första tillvägagångssättet i elementära fysikproblem är att anta att alla objekt uppträder som en specifik massa, det vill säga det saknar dimensioner och hela massan är koncentrerad i en enda punkt. Detta är giltigt för en låda, en bil, en planet eller en subatomisk partikel. Denna modell är känd som partikelmodell.

Figur 1. I höjden hoppar idrottaren dem så att dess tyngdpunkt är utanför kroppen. Källa: Pixabay

Naturligtvis är detta en metod, som ger mycket bra resultat för många applikationer. Det är inte en lätt uppgift att överväga det individuella beteendet hos de tusentals och miljoner partiklar som alla objekt kan innehålla.

De verkliga dimensionerna av saker bör dock beaktas om du vill. Eftersom vi vanligtvis är i omedelbar närhet av jorden är den alltid nuvarande kraften på någon kropp precis vikten.

[TOC]

Överväganden för att hitta tyngdpunkten 

Om kroppsstorleken kommer att beaktas, där vikten kommer att appliceras specifikt? När du har ett kontinuerligt objekt godtyckligt är dess vikt en Distribuerad kraft mellan var och en av dess beståndsdelar.

Låt dessa partiklar m₁, m₂, m₃... var och en av dem upplever sin motsvarande gravitationskraft m₁g, m₂g, m₃G ..., alla parallella. Detta är så, eftersom jordens gravitationsfält anses vara konstant i de allra flesta fall, med tanke på att föremål är små jämfört med planetens storlek och är nära dess yta.

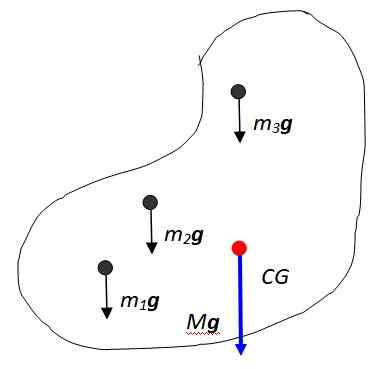figur 2. Objektets vikt är en distribuerad massa. Källa: Självgjord.

Vektorsumman av dessa krafter resulterar i objektets vikt, tillämpad på den punkt som kallas tyngdpunkten som betecknas i figuren som CG, som sedan sammanfaller med Masscentrum. Masscentret är i sin tur den punkt där hela massan kan betraktas som koncentrerad.

Den resulterande vikten har storlek Mg var M Det är objektets totala massa, och naturligtvis riktas den vertikalt mot jordens centrum. Sumory Notation är användbar för att uttrycka kroppens totala kropp:

Symmetriska och homogena föremål, som motsvarar deras densitet är enhetlig, har deras tyngdpunkt i det geometriska centrumet: kuber, parallellepipeds, ringar, däck eller sfärer.

Tyngdpunkten matchar inte alltid en materiell punkt. Till exempel är CG för en båge i dess geometriska centrum, där det inte finns någon deg i sig själv. Trots det, om du vill analysera de krafter som verkar på en båge, måste vikten tillämpas på denna exakta punkt.

I vilka fall där objektet är godtyckligt, om det är homogent, kan dess masscentrum fortfarande beräknas genom att hitta centroid o baricentro i figuren.

Kan tjäna dig: Merkurius (Planet)

Hur beräknas tyngdpunkten?

I princip om tyngdpunkten (CG) och masscentret (CM) sammanfaller när gravitationsfältet är enhetligt, kan CM beräknas och på den applicera vikten.

Tänk på två fall: den första är ett där massfördelningen är diskret; Det vill säga, du kan räkna varje massa som bildar systemet och tilldelar ett nummer I, som gjordes i föregående exempel.

Koordinaterna för masscentret för en diskret massfördelning är: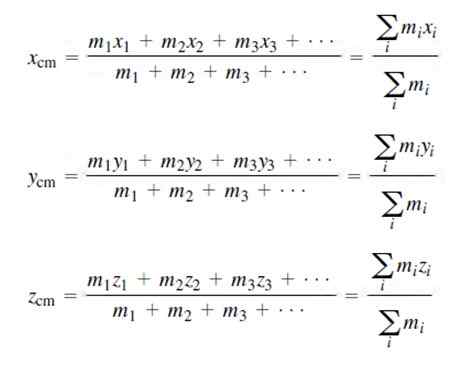

Naturligtvis motsvarar summan av alla massor den totala massan för M -systemet, såsom anges ovan.

De tre ekvationerna reduceras till en kompakt form när man överväger vektorn r_centimeter o Positionvektor för masscentret:

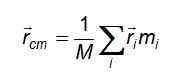
Och vid en kontinuerlig massfördelning, där partiklarna är av differentiell storlek och inte kan särskiljas för att räkna dem, ersätts summan av en integral som görs om den volym som upptar av objektet i fråga:

Var r Det är positionsvektorn för en differentiell massa Dm Och definitionen av masstäthet för att uttrycka massdifferensen har gjorts Dm finns i en volymskillnad Dv:

Objektets densitet kan vara konstant, i vilket fall kommer det ut ur integralen, eller att vara en funktion av de rumsliga koordinaterna och vi måste veta dess beroende av (x, y, z) för att lösa integralen.

Egenskaper

Några viktiga överväganden om masscentret är följande:

- Även om ett referenssystem krävs för att etablera positioner beror inte massans centrum på valet som är gjord av systemet, eftersom det är en egenskap hos objektet.

- När objektet har en axel eller ett symmetriplan är masscentret på nämnda axel eller plan. Dra fördel av denna omständighet sparar beräkningstid.

- Alla externa krafter som verkar på objektet kan tillämpas på masscentret. Efter spåret av denna punkt ger en global uppfattning om objektets rörelse och underlättar arbetet med att studera dess beteende.

-Hitta tyngdpunkten i en kropp i statisk balans

Anta att kroppen till den föregående figuren är i statisk balans är.

Figur 3. Schema för att beräkna viktmomentet med avseende på punkt eller.

Momentet för netto torsion med avseende på O, enligt figur 3 är: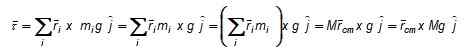En kraft F som appliceras vertikalt upp i tyngdpunkten (eller även över eller under, på axeln som passerar genom den) skulle ge en motsatt torsion som skulle förhindra rotation av objektet och upprätthålla rotationsbalansen. Storleken på F väljs så att objektet inte heller överförs och på detta sätt kommer vi att ha det i statisk jämvikt.

Kan tjäna dig: böljande optik

-Löst exempel

En tunn stång med enhetligt material har en längd på 6 m och väger 30 n. I slutet hängs en 50 n väster och en annan av 20 n i sin högra ände. Hitta: a) Storleken på den stigande kraften som krävs för att upprätthålla stångens balans, b) tyngdpunkten i uppsättningen.

Lösning

Kraftsdiagrammet visas i följande figur. Stångens vikt appliceras i tyngdpunkten, som sammanfaller med dess geometriska centrum. Den enda dimensionen av det bar som beaktas är dess längd, eftersom uttalandet informerar om att det är tunt.

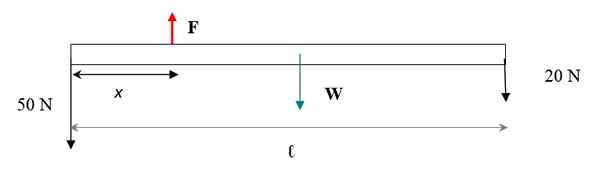Figur 4. Pàra la barra diagram.

För att bar + viktsystemet ska förbli i översättningsbalansen måste summan av krafterna vara noll. Krafterna är vertikala, om vi överväger med ett skylt + och ner med ett tecken - då:

F- 50- 20-30 n = 0

F = 100 n

Denna styrka garanterar översättningsbalansen. Att ta momenten av vridning av alla krafter angående en axel som passerar genom systemets vänstra ände och tillämpa definitionen:

t = r x f

Momenten för alla dessa krafter med avseende på den valda punkten är vinkelrätt mot stångens plan:

t_F = xf = 100x

t_W = -(l/2) mg = -3m . 30 n = -90 n.m

t₁ = 0 (Eftersom kraften på 50 n passerar genom den valda vändaxeln och inte utövar ögonblick)

t₂ = -Lf₂ = 6 m . 20 n = -120 n.m

Därför:

100 x -90 -120 n.m = 0

x = 2.10 m

Tyngdpunkten för barstången + vikter ligger vid 2.10 meter från den vänstra änden av baren.

Skillnad med massa centrum

Tyngdpunktens centrum sammanfaller med masscentrum, så länge som landets gravitationsfält är konstant för alla punkter i objektet som ska övervägas. Jordens gravitationsfält är inget annat än det välkända och bekanta värdet på g = 9.8 m/s² riktad vertikalt ner.

Även om värdet av G upplever variationer med latitud och höjd påverkar de vanligtvis inte föremål som de flesta gånger behandlas. Mycket annorlunda skulle vara om det betraktas som en stor kropp i närheten av jorden, till exempel en asteroid som skulle nära planeten.

Asteroiden har sitt eget masscentrum, men dess tyngdpunkt skulle inte längre behöva sammanfalla med detta, sedan g Det skulle förmodligen uppleva betydande variationer i storlek, med tanke på asteroidens storlek och att vikterna för varje partikel kanske inte är parallella.

En annan grundläggande skillnad är att masscentret är oavsett om det finns en kraft som kallas applicerad vikt på objektet. Det är en inre egenskap hos objektet som avslöjar hur dess massa fördelas i förhållande till dess geometri.

Kan tjäna dig: vad är den dielektriska konstanten?

Masscentret finns både om det finns vikt som tillämpas som om inte. Och ligger i samma position även om objektet överförs till en annan planet där gravitationsfältet är annorlunda.

Å andra sidan är tyngdpunkten tydligt kopplat till tillämpningen av vikt, som vi har kunnat uppskatta under tidigare stycken.

Tyngdkraftsexempel

Tyngdpunkt i oregelbundna föremål

Det är väldigt lätt att ta reda på var tyngdpunkten i ett oregelbundet föremål är som en kopp. Först är den upphängd från vilken punkt som helst och därifrån ritas en vertikal linje (i figur 5 är det Fuchsia -linjen i den vänstra bilden).

Sedan är den upphängd från en annan punkt och en ny vertikal (turkos linje i rätt bild) ritas. Korsningen mellan båda linjerna är tyngdpunkten i koppen.

Figur 5 . CG -plats för en kopp. Källa: Modifierad Pixabay.

Föremål

Låt oss analysera stabiliteten i en lastbil som cirkulerar längs vägen. När tyngdpunkten ligger över lastbilens bas kommer den inte att hälla. Bilden till vänster är den mest stabila positionen.

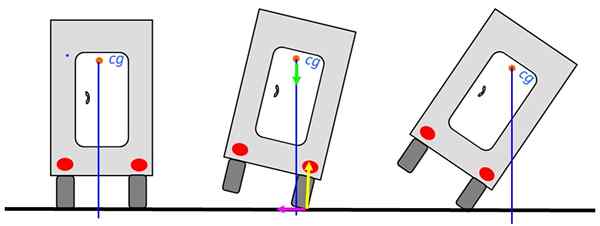Figur 6. Lastbil. Källa: Självgjord.

Även när lastbilen lutar till höger kan återgå till det stabila jämviktsläget, som i ritningen av mediet, eftersom den vertikala fortfarande passerar genom basen. Men när denna linje passerar utanför lastbilen kommer.

Diagrammet visar krafterna vid stödpunkten: det normala i gult, vikten i grönt och den statiska friktionen till vänster i Fuchsia. Normal och Rubb. Därför kommer de inte att bidra till att dumpa lastbilen.

Vikten kvarstår, som utövar ett ögonblick av vridning, lyckligtvis i anti -horary -meningen och som tenderar att återgå till lastbilen till dess jämviktsposition. Observera att den vertikala linjen passerar genom stödytan, som är däcket.

När lastbilen är i den extrema höger, tiden för vridning av viktförändringar och blir i en spänd riktning. Att inte kunna motverkas vid en annan tidpunkt kommer lastbilen att hälla.

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.  247-253.
2. Giancoli, D.  2006. Fysik: Principer med applikationer. 6: e ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Fysisk. Vul. 1. 3: e upplagan. på spanska. Kontinentala redaktionella företag s.TILL. av C.V. 331-341.
4. Rex, a. 2011. Fysikens grunder. Pearson.146-155.
5. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.340-346.