Växlande aktuella kretsstyper, applikationer, exempel

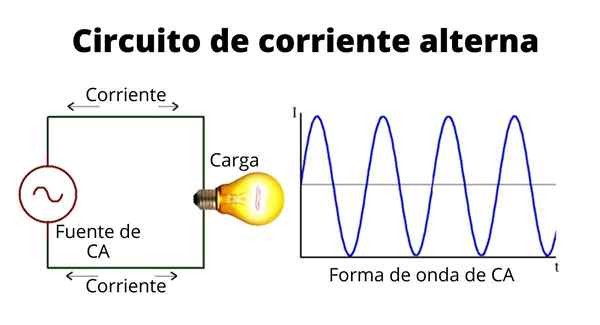
De växlande strömkretsar antingen Ca -kretsar De består av kombinationer av resistiva, induktiva och kapacitiva element, i kombination med en alternativ spänningskälla, som vanligtvis är sinusformad.

Vid applicering av spänningen upprättas en variabel ström under en kort tid, kallad övergångsström, vilket ger plats för sinusformad stationär ström.

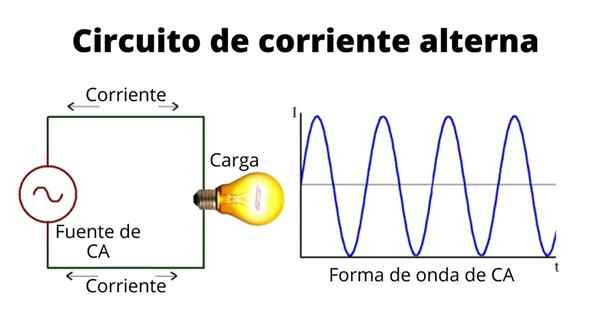En växlande strömkrets

Den sinusformade strömmen har värden som växlar mellan positiva och negativa och ändrar till regelbundna intervaller bestämda av en tidigare etablerad frekvens. Strömans form uttrycks som:

I (t) = i_m Sen (ωt --φ)

Där jag_m Det är den maximala strömmen eller amplituden för strömmen är frekvensen, t Det är dags och φ fasskillnaden. De enheter som vanligtvis används för strömmen är förstärkarna (a) och dess undermultiplar, såsom milliamperium och mikroamperium.

För sin del mäts tiden på några sekunder, för frekvens är Hertzios eller Hertz, förkortade Hz, medan fasskillnaden är en vinkel som vanligtvis mäts i radianer, även om den ibland förekommer i grader. Varken dessa eller radianerna betraktas som enheter.

Symbol som används för alternativ spänningskälla

Ofta symboliseras den alternativa spänningen med vågen inuti cirkeln, för att skilja den från den direkta spänningen, symboliserad av de två ojämlika och parallella linjerna.

[TOC]

Typer av växlande strömkretsar

Det finns många typer av växlande strömkretsar, börjar med de enklaste kretsarna som visas i följande figur. Från vänster till höger har de:

-Respekt med motstånd R

-Krets med spole L

-Krets med kondensator C.

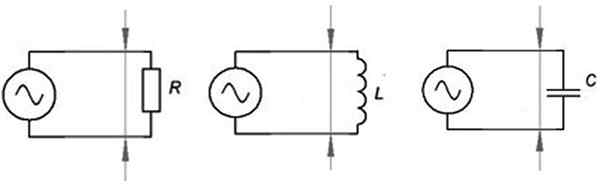Från vänster till höger: resistiv, induktiv och slutkapacitetskrets. Källa: f. Zapata.

Krets med resistivt element

I kretsen med ett motstånd R anslutet till en alternativ spänningskälla är motståndsspänningen v_R = V_m Sen ωt. Av Ohm Law, som också är giltig för rent resistiva kretsar av växlande ström:

V_R = Jag_R∙ r

Därför den maximala strömmen i_m = V_m /R.

Både strömmen och spänningen är i fas, vilket innebär att de når sina maximala värden, liksom 0, samtidigt.

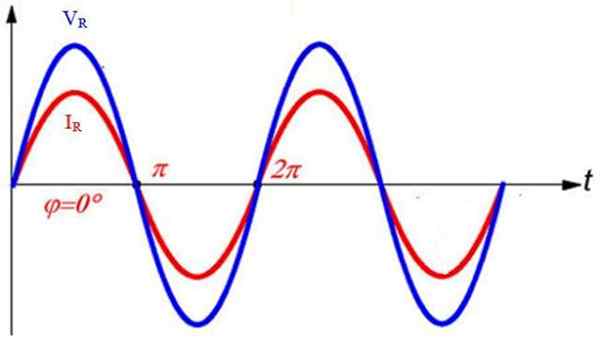I en rent resistiv växlande strömkrets är ström och motstånd i fas. Källa: f. Zapata.

Induktiv elementkrets

I spolen l är spänningen v_L = V_m Sen ωt och är relaterad till strömmen i induktorn genom ekvationen:

Integrera:

Av egenskaper av trigonometriska skäl, i_L Det är skrivet i termer av synd ωt som:

Yo_L = Jag_m synd (ωt - ½ π)

Kan tjäna dig: naturliga satelliter

Sedan är spänningen och strömmen föråldrad, den senare försenade ½ π = 90º med avseende på spänningen (strömmen börjar innan, som är t = 0 s utgångspunkt). Detta ses i följande figur jämfört med Sinusoid av I_L och den av V_L:

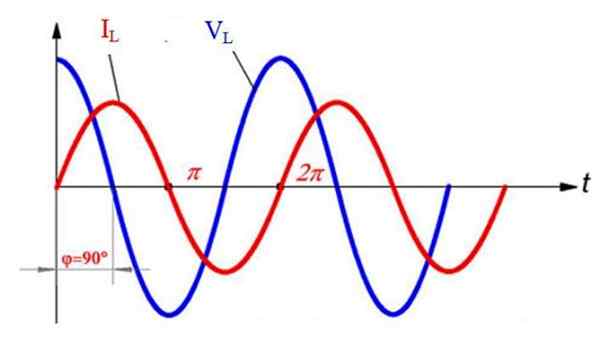Alternativ spänning och ström i en rent induktiv växelströmskrets. Källa: f. Zapata.

Induktiv reaktans

Induktiv reaktans definieras som x_L = Ωl, ökar ofta och har resistensdimensioner, därför i analogi med Ohms lag:

V_L = Jag_L ∙ x_L

Krets med kapacitivt element

För en casser C ansluten till en växlande nuvarande källa uppfylls det::

Q = c ∙ v_C = C ∙ v_m Sen ωt

Strömmen i kondensorn härstammar lasten med avseende på tid:

Yo_C= ωc ∙ V_m cos ωt

Men cos ωt = synd (ωt + ½ π), då:

Yo_C = Ωcv_m synd (ωt+ ½ π)

I detta fall går de nuvarande framstegen till spänningen i ½ π, vilket kan ses från grafiken.

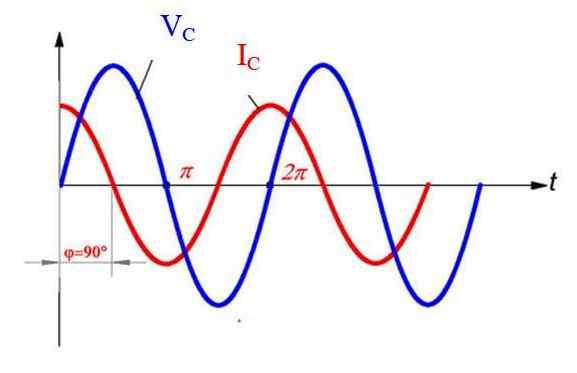Spänning och ström i den alternativa kretsen med rent kapacitivt element. Källa: f. Zapata.

Kapacitiv reaktans

Den kapacitiva reaktansen kan skrivas x_C = 1/ωc, minskar med frekvens och har också motståndsenheter, det vill säga ohm. På detta sätt är Ohms lag så här:

V_C = X_C.Yo_C

Ansökningar

Michael Faraday (1791-1867) var den första som erhöll en ström som regelbundet ändrade sin betydelse, genom sina induktionsexperiment, även om endast likström under de första dagarna användes endast strömströmmen användes.

I slutet av 1800 -talet inträffade strömmarna för strömmarna, mellan Thomas till. Edison, försvarare för användningen av likström och George Westinghouse, anhängare av den växlande strömmen. Slutligen var detta den som vann efter ekonomi, effektivitet och enkel överföring med mindre förluster.

Av denna anledning till datum är den nuvarande som kommer till hem och industrier växelström, även om användningen av likström aldrig försvann helt.

Den växlande strömmen används för nästan allt, och i många tillämpningar är den ständiga riktningsförändringen för den växlande strömmen inte relevant, såsom glödlampor, järn eller matlagningshorn, eftersom uppvärmningen av det resistiva elementet inte beror på Riktning av rörelsens rörelse.

Å andra sidan är det faktum att den nuvarande förändringen som betyder med en viss frekvens grunden för elmotorer och olika mer specifika applikationer, till exempel följande:

Det kan tjäna dig: ljudutbredning

Pelfming kretsar

Kretsarna som består av en alternativ källa ansluten till ett motstånd och en seriekondensator kallas RC -seriekretsar och används för att eliminera oönskade linjer i en annan krets, eller också lägga till en viss speciell effekt till detta.

De fungerar också som spänningsdelar och för att stämma in radiostationer (se exempel 1 i nästa avsnitt).

Bryggtypkretsar

Bryggkretsar som matas med växelström kan användas för att mäta kapacitet eller induktans, på samma sätt som Wheatstone Bridge används, en välkänd likströmskrets som kan mäta värdet på ett okänt motstånd.

Exempel på växlande strömkretsar

I de föregående avsnitten beskrivs de enklaste växlande strömkretsarna, även om de grundläggande elementen som beskrivs ovan, liksom andra lite mer komplexa som dioder, förstärkare och transistorer, för att nämna några, kan kombineras för att få olika effekter.

Exempel 1: RLC -krets

En av de vanligaste kretsarna i Växelström Det är den som innehåller en motstånd R, en spole eller induktor L och en kondensator eller kondensor C -serie med en växlande strömkälla.

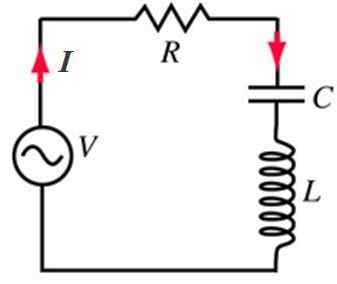RLC -krets i serie matad med en växlande nuvarande källa. Källa: f. Zapata.

RLC -seriekretsarna svarar särskilt på frekvensen för den alternativa källan som de matas. Det är därför en av de mest intressanta applikationerna är som radioinställda kretsar.

En radiosignal genererar ofta en ström med samma frekvens i en krets speciellt utformad för att fungera som mottagare, och amplituden för denna ström är maximal om mottagaren är inställd med den frekvensen, genom en effekt som kallas resonans.

Mottagningskretsen fungerar som en tuner eftersom den är utformad så att signalerna för oönskade frekvenser genererar mycket små strömmar, som inte upptäcks av radiohögtalarna och därför inte är hörbara. Å andra sidan, till resonansfrekvensen, når amplituden hos strömmen ett maximalt och sedan hörs signalen tydligt.

Resonansfrekvensen uppstår när kretsens induktiva och kapacitiva reaktanser utjämnas:

X_L = X_C

1/ωc = ωl

Ω² = 1/lc

Radiostationen med frekvenssignalen ω sägs vara "inställd", och värdena på L och C väljs för den vissa frekvensen.

Det kan tjäna dig: Normal ansträngning: vad den består av, hur det beräknas, exempel

Exempel 2: RLC -kretsen parallellt

RLC -kretsar parallellt har också vissa svar enligt källfrekvensen, som beror på reaktansen för vart och ett av elementen, definierade som orsaken mellan spänningen och strömmen.

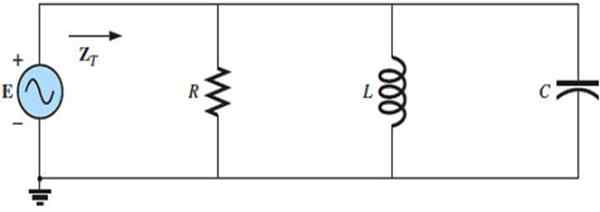RLC -kretsen parallellt ansluten till en växlande strömkälla. Källa: f. Zapata.

Träning löst

I LRC -kretsen i serie 1 i föregående avsnitt är motståndet värt 200 ohm, induktans 0.4 timmar och kondensorn är 6 μF. För sin del är strömförsörjningen en alternativ amplitudspänning lika med 30 V, ofta 250 rad/s. Det uppmanas att hitta:

a) Reaktanserna för varje element

b) Värdet på kretsimpedansmodulen.

c) strömmen

Lösning till

De respektive reaktanserna beräknas med formlerna:

X_C = 1/ωc = 1/(250 rad/s x 6 x10^-6 F) = 666,67 ohm

X_L = Ωl = 250 rad/s x 0.4 h = 100 ohm

Och motståndsreaktansen motsvarar dess värde i ohm:

X_R = R = 200 ohm

Lösning B

Impedans Z definieras som orsaken mellan spänningen och strömmen i kretsen, antingen i serie eller parallellt:

Z = v_m / Yo_m

Impedans mäts i ohm, såväl som motstånd eller reaktans, men hänvisar till oppositionen mot passagen av induktans och kondensatorer, med tanke på att utöver deras speciella effekter, såsom försening eller avancerar till spänningen, också de har ett visst internt motstånd.

Det kan demonstreras att för RLC -seriekretsen ges impedansmodulen av:

Vid utvärdering av värdena i uttalandet erhålls det:

Lösning C

Av:

Z = v_m / Yo_m

Det måste;

Yo_m = V_m / Z = 30V / 601 ohm = 0.05 a.

Intresse teman

Skillnader mellan växlande och likström

Referenser

1. Alexander, c. 2006. Elektriska kretsfundament. 3: e. Utgåva. MC Graw Hill.
2. Boylestad, r. 2011. Introduktion till kretsanalys.2: a. Utgåva. Pearson.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 6. Elektromagnetism. Redigerad av Douglas Figueroa (USB).
4. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1. Pearson.
5. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.