Konduktansformler, beräkning, exempel, övningar

De ledningsförmåga Från en förare definieras den som lätthet den måste missa den elektriska strömmen. Det beror inte bara på materialet som används för dess tillverkning, utan också på dess geometri: längd och område på tvärsnittet.

Symbolen som används för konduktans är G och är den omvända elektriska motståndet R, en något mer bekant storlek. Den internationella systemenheten om för konduktans är det omvända av Ohmio, betecknad som ω^-1 och få namnet på Siemens (S).

Figur 1. Konduktans beror på materialet och förarens geometri. Källa: Pixabay.

Andra termer som används i el, som låter som liknar konduktans och är relaterade är ledningsförmåga och den körning, Men de borde inte vara förvirrade. Den första av dessa termer är en inre egenskap hos ämnet som föraren tillverkas och den andra beskriver flödet av elektrisk laddning genom den.

För en elektrisk ledare med konstant tvärsnitt av området TILL, längd L och konduktivitet σ, Konduktansen ges av:

G = σ.TILL

Till större konduktivitet, större konduktans. Ju större tvärsektionsområdet, desto lättare för föraren att låta strömmen passera. Tvärtom, ju större längd l, desto lägre konduktans, eftersom de nuvarande bärarna förlorar mer energi i längre resor.

[TOC]

Hur beräknas konduktans?

Konduktans G för en ledare med ett konstant tvärsnittsområde beräknas enligt ekvationen som anges ovan. Detta är viktigt, för om tvärsnittet inte är konstant måste den integrerade beräkningen användas för att hitta både motstånd och konduktans.

Eftersom det är det omvända av motståndet, kan konduktans g beräknas med att veta att:

Kan tjäna dig: kvantmekanisk modell av atomen

G = 1/r

I själva verket kan en förares elektriska motstånd mätas direkt med en multimeter, en apparat som också mäter ström och spänning.

Förareenheter

Som nämnts i början är enheten för konduktans i det internationella systemet Siemens (er). Det sägs att en förare har en konduktans på 1 s om strömmen som korsar den ökas med 1 amperio för varje volt av potentialskillnad.

Låt oss se hur det är möjligt genom Ohms lag, om det är skrivet när det gäller konduktans:

V = i.R = i/g

Var V Det är spänningen eller den potentialskillnaden mellan förarens ändar och Yo Nuvarande intensitet. När det gäller dessa storlekar kvarstår formeln så här:

G = i/v

Tidigare var enheten för konduktans Mho (ohm skriven bakåt) betecknas som ʊ, som är ett kapital eller inverterad omega. Denna notation avvisades och ersattes av Siemens För att hedra den tyska ingenjören och uppfinnaren Ernst von Siemens (1816-1892), en pionjär för telekommunikation, men båda är helt likvärdiga.

1 MHO = 1 Siemens = 1 A/V (Ampere/Volt)

figur 2. Konduktans kontra motstånd. Källa: Wikimedia Commons. Think Tank [CC av 3.0 (https: // CreativeCommons.Org/licenser/av/3.0)]

I andra mätsystem Statsiemens (statistik) (i CGS eller Centimeter-gram-sekundssystemet) och Absiemens (abs) (Elektromagnetiskt CGS -system) med "S" i slutet, utan att indikera singular eller pluralis, eftersom de kommer från rätt namn.

Vissa ekvivalenser

1 statistik = 1.11265 x 10 ^-12 Siemens

1 ABS = 1 x 10⁹ Siemens

Exempel

Som nämnts tidigare, med motstånd, är konduktans omedelbart känt när man bestämmer det omvända eller ömsesidiga värdet. På detta sätt motsvarar en elektrisk motstånd på 100 ohm.01 Siemens, till exempel.

Under ytterligare två exempel på konduktansanvändning:

Kan tjäna dig: magnetisk chock: enheter, formler, beräkning, exempel

Konduktivitet och konduktans

De är olika termer, som redan anges. Konduktiviteten är en egenskap hos ämnet som föraren tillverkas, medan föraren är typisk för föraren.

Konduktivitet kan uttryckas i termer av G som:

σ = g.(DE)

Därefter en tabell med konduktivitet för ofta använda ledande material:

bord 1. Konduktivitet, resistivitet och värmekoefficient för vissa ledare. Referenstemperatur: 20 ºC.

Metall	σ x 106 (EDER)	ρ x 10-8 (Ω.m)	α ºC-1
Silver	62.9	1.59	0.0058
Koppar	56.5	1.77	0.0038
Guld	41.0	2.44	0.0034
Aluminium	35.4	2.82	0.0039
Volfram	18.0	5.60	0.0045
Järn	10.0	10.0	0.0050

Motstånd i parallellt

När de har kretsar med parallella motstånd är det ibland nödvändigt att få motsvarande motstånd. Att känna till motsvarande motståndsvärde gör det möjligt att ersätta uppsättningen motstånd för ett enda värde.

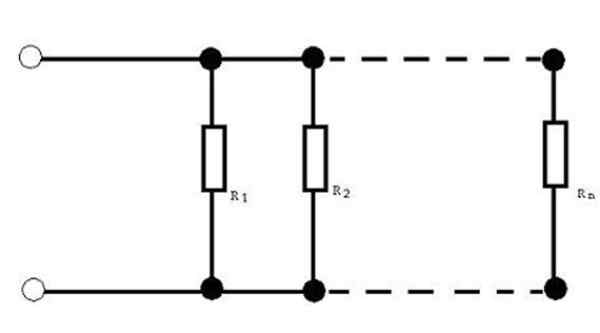Figur 3. Parallellförening i parallellt. Källa: Wikimedia Commons. Ingen maskinläsbar författare tillhandahållen. Sotake antog (baserat på upphovsrättsanspråk). [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]].

För denna motståndskonfiguration ges motsvarande motstånd av:

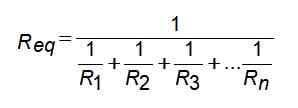
Men om du skriver när det gäller konduktans är det mycket förenklat: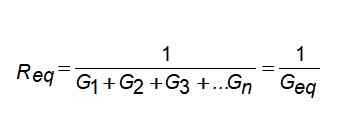Därför:

G_eq = G₁ + G₂ + G₃ +... G_n

Det vill säga, likvärdig konduktans är summan av ledningar. Om du vill veta motsvarande motstånd är resultatet helt enkelt investerat.

Övningar

- Övning 1

a) Skriv ohms lag när det gäller konduktans.

b) Hitta konduktansen för en 5 volframtråd på 5.4 cm lång och 0.15 mm i diameter.

c) Nu passeras en ström på 1.5 A för tråden. Vad är den potentiella skillnaden mellan ändarna på denna förare?

Kan tjäna dig: de 31 typerna av kraft i fysik och deras egenskaper

Lösning till

Från de föregående avsnitten du måste:

V = i/g

G = σ.TILL

Genom att ersätta det senare i det första förblir det så här:

V = i /(σ.A/l) = i.L / σ.TILL

Var:

-Jag är intensiteten i strömmen.

-L är förarens längd.

-σ är konduktivitet.

-A är området för tvärsnittet.

Lösning B

För att beräkna konduktansen för denna volframtråd krävs dess konduktivitet, som finns i tabell 1:

σ = 18 x10⁶ EDER

L = 5.4 cm = 5.4 x 10^-2 m

D = 0. 15 mm = 0.15 x 10^-3 m

A = π.D² / 4 = π . (0.15 x 10^-3 m)² / 4 = 1.77 x 10^-8 m²

Ersätta i ekvationen du har:

G = σ.A/L = 18 x10⁶ EDER . 1.77 x 10^-8 m² / 0.15 x 10^-3 M = 2120.6 s.

Lösning C

V = i/g = 1.5 A / 2120.6 s = 0.71 mV.

- Övning 2

Hitta motsvarande motstånd i följande krets och veta att jag_antingen = 2 a, beräkna i_x och kraften som sprids av kretsen:

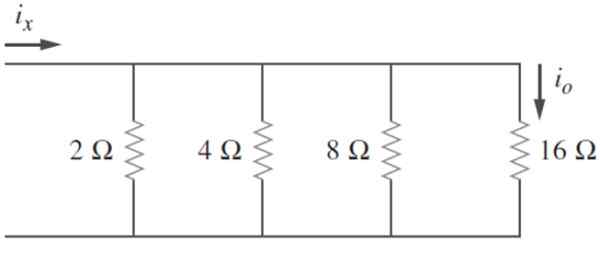Figur 4. Krets med parallella motstånd. Källa: Alexander, C. 2006. Elektriska kretsfundament. 3: e. Utgåva. McGraw Hill.

Lösning

Motstånd listas: r₁= 2 Ω; R₂= 4 Ω; R₃= 8 Ω; R₄= 16 Ω

Konduktansen beräknas sedan i varje fall: g₁ = 0.5 ʊ; G₂ = 0.25 ʊ; G₃ = 0.125 ʊ; G₄ = 0.0625 ʊ

Och slutligen lägger de till som anges tidigare för att hitta motsvarande konduktans:

G_eq = G₁ + G₂ + G₃ +... G_n = 0.5 ʊ + 0.25 ʊ + 0.125 ʊ + 0.0625 ʊ = 0.9375 ʊ

Därför r_eq = 1.07 Ω.

Spänningen i r₄ är v₄ = jag_antingen. R₄ = 2 a . 16 Ω = 32 V, och är densamma för alla motstånd, eftersom de är anslutna parallellt. Då är det möjligt att hitta de strömmar som cirkulerar för varje motstånd:

-Yo₁ = V₁ /R₁ = 32 v / 2 Ω = 16 a

-Yo₂ = V₂ /R₂ = 32 V / 4 Ω = 8 a

-Yo₃ = V₃ /R₃ = 32 v / 8 Ω = 4 a

-Yo_x = jag₁ +  Yo₂ +  Yo₃ + Yo_antingen = 16 + 8 + 4 + 2 a = 30 a

Slutligen är den spridda kraften P:

P = (i_x)². R_eq = 30 till x 1.07 Ω = 32.1 w

Referenser

1. Alexander, c. 2006. Elektriska kretsfundament. 3: e. Utgåva. McGraw Hill.
2. Megaampere / millivolt till absiemens kalkylatorkonvertering. Återhämtat sig från: Pinkbird.org.
3. Garcia, L. 2014. Elektromagnetism. 2: a. Utgåva. Industrisantare. Colombia.
4. Riddare, r.  2017. Fysik för forskare och teknik: En strategistrategi.  Pearson.
5. Rull, D. 1990. Fysisk. El, magnetism och optik. Volym II. Redaktör.
6. Wikipedia. Elektrisk konduktans. Återhämtad från: är.Wikipedia.org.
7. Wikipedia. Siemens. Återhämtad från: är.Wikipedia.org.