Ohm lag och formel, beräkning, exempel, övningar

De Ohms lag, I sin makroskopiska form indikerar det att spänningen och intensiteten hos strömmen i en krets är direkt proportionell, varvid motståndet är proportionalitetskonstanten. Ohms lag, som anger dessa tre storlekar som V, I respektive R, fastställer att: V = i.R.

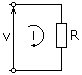
På samma sätt generaliseras Ohms lag för att inkludera kretselement som inte är rent resistiva i växlande strömkretsar, vilket antar enligt följande: V = i. Z.

Figur 1. Ohms lag är tillämplig på många kretsar. Källa: Wikimedia Commons. Tlapicka [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)]

Var Z Det är impedansen, som också representerar oppositionen mot passagen av den växlande strömmen med ett kretselement, till exempel en kondensor eller en induktans.

Det bör noteras att inte alla kretsmaterial och element uppfyller Ohms lag. Till de där det är giltigt kallas element ohmisk, Och där det inte är uppfyllt kallas de No-ohmic eller icke -linjär.

Vanliga elektriska motstånd är ohmiska, men dioder och transistorer är inte, eftersom förhållandet mellan spänning och ström inte är linjärt i dem.

Ohms lag är skyldig sitt namn till den tyska fysikern och matematisk. Till hans ära har enheten för elektrisk motstånd i det internationella systemet utsetts: The Ohm, som också uttrycks av den grekiska bokstaven Ω.

[TOC]

Hur beräknas det?

Även om den makroskopiska formen av Ohms lag är den mest kända, eftersom den länkar belopp som lätt är mätbara i laboratoriet, Mikroskopisk form relaterar två viktiga vektorkvantiteter: det elektriska fältet OCH och strömtäthet J:

J = σ.OCH

Där σ är materialets elektriska konduktivitet, en egenskap som indikerar den lätthet den måste driva aktuell. För sin del J Det är en vektor vars storlek är kvoten mellan nuvarande intensitet I och det tvärsnitt som det cirkulerar.

Det kan tjäna dig: ytliga vågor: egenskaper, typer och exempel

Det är logiskt att anta att det finns en naturlig koppling mellan det elektriska fältet i ett material och den elektriska strömmen som cirkulerar genom det, till exempel den största vanligare.

Men strömmen är inte en vektor, eftersom den inte har en adress i rymden. Istället vektorn J Det är vinkelrätt - eller normalt - till förarens tvärsektionsarea och dess betydelse är den för strömmen.

Från denna form av Ohms lag nås den första ekvationen, förutsatt att en längdförare och tvärsnitt A, och ersätter storleken på J och OCH förbi:

J = i/a

E = v/ℓ

J = σ.E → I/A = σ. (V/ℓ)

V = (ℓ/σ.TILL).Yo

Det omvända konduktiviteten kallas resistivitet Och det betecknas med den grekiska bokstaven ρ:

1/ σ = ρ

Därför:

V = (ρℓ/ a).I = r.Yo

Förarens motstånd

I ekvationen V = (ρℓ/ a).Yo, Konstanten (ρℓ/ a) Det är därför motstånd:

R = ρℓ/ a

Förarmotstånd beror på tre faktorer:

-Hans resistivitet ρ, typisk för materialet som han är tillverkad.

-Längden ℓ.

-Område A i dess tvärsnitt.

En större ℓ, större motstånd, eftersom nuvarande bärare har fler möjligheter att kollidera med de andra partiklarna inuti föraren och förlora energi. Och tvärtom, till större a, är det lättare för nuvarande bärare att röra sig på ett ordnat sätt av materialet.

Slutligen, i molekylstrukturen för varje material ligger den lätthet som ett ämne låter den elektriska strömmen passera. Således är metaller som koppar, guld, silver och platina, med låg resistivitet, goda ledare, medan trä, gummi och olja inte är det, så de har större resistivitet.

Exempel

Här är två illustrativa exempel på ohms lag.

Experiment för att kontrollera ohms lag

En enkel upplevelse illustrerar Ohms lag, för detta är ett stycke ledande material, en variabel spänningskälla och en multimeter behövs.

Kan tjäna dig: tryckmätare

Bland ändarna på det ledande materialet upprättas en spänning V som bör variera gradvis. Med den variabla effektkällan kan värdena på nämnda spänning fixeras, som mäts med multimetern, liksom den ström jag cirkulerar av föraren.

Paret i värden V och jag spelas in i en tabell och med dem är en graf på millimeter papper byggt. Om den resulterande kurvan är en linje är materialet ohmiskt, men om det är någon annan kurva är materialet icke -hmiskt.

I det första fallet kan linjens lutning bestämmas, vilket motsvarar förarens motstånd eller med dess omvända, konduktansen.

I följande bild representerar Blue Line en av dessa grafik för ett ohmiskt material. Samtidigt är gula och röda kurvor av icke-oshmiska material, till exempel en halvledare, till exempel.

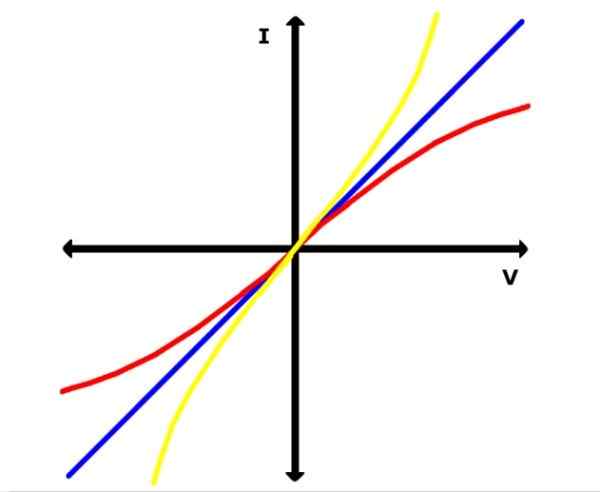figur 2. Graf I Vs. V för ohmiska material (blå rak) och icke-oosohmiska material. Källa: Wikimedia Commons.

Hydraulisk analogi av ohms lag

Det är intressant att veta att den elektriska strömmen i OHM -lagen har ett liknande beteende på ett visst sätt som vatten som cirkulerar genom ett rör. Den engelska fysikern Oliver Lodge var den första som föreslog simulering av aktuellt beteende genom hydrauliska element.

Till exempel representerar rören ledarna, eftersom vattnet cirkulerar genom dem och de nuvarande bärarna genom det sista. När det finns en minskning av röret är vattenpassagen svår, så detta skulle motsvara elektrisk motstånd.

Tryckskillnaden vid två ändar av röret gör att vatten kan flyta, vilket ger en skillnad i höjder eller en vattenpump, och analogt är potentialskillnaden (batteriet) den som håller den rörliga belastningen, motsvarande flöde eller volym av vatten per tidsenhet.

Det kan tjäna dig: konvektionsvärmeöverföring (med exempel)

En kolvpump skulle representera rollen som en alternativ spänningskälla, men fördelen med att sätta en vattenpump är att den hydrauliska kretsen skulle stängas, eftersom en elektrisk krets bör vara att flöda strömmen.

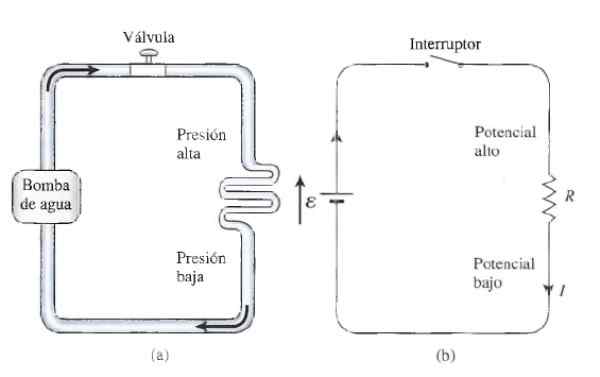Figur 3. Hydraulisk analogi för ohm lag: i a) ett vattenflödessystem och i b) en enkel resistiv krets. Källa: Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.

Motstånd och switchar

Motsvarigheten till en switch i en krets skulle vara en passage -nyckel. Det tolkas på detta sätt: om kretsen är öppen (stängd passage) kan strömmen såväl som vattnet inte flyta.

Å andra sidan, med den stängda omkopplaren (helt öppen stegnyckel) kan både strömmen och vattnet cirkulera utan problem av föraren eller röret.

Passningsknappen eller ventilen kan också representera ett motstånd: när nyckeln öppnas helt motsvarar den att ha ett nollmotstånd eller kortslutning. Om det stängs alls är det som att ha den öppna kretsen, medan delvis stängd är det som att ha ett motstånd mot ett visst värde (se figur 3).

Övningar

- Övning 1

Det är känt att en elektrisk platta kräver 2 A vid 120 V för att fungera korrekt. Vad är ditt motstånd?

Lösning

Motståndet rensas från Ohms lag:

R = v/ i = 120 v/ 2 a = 60 Ω

- Övning 2

En tråd med 3 mm diameter och 150 m lång har 3 3.00 Ω vid 20 ° C. Hitta materialets resistivitet.

Lösning

Ekvationen R = ρℓ/ a är lämplig, Därför är det nödvändigt att först hitta tvärsnittets område:

A = π(D/2)² = π (3 x 10^-3 m/2)² = 4.5π x 10 ^-6 m²

Slutligen när du ersätter får du:

ρ = a.R /ℓ = 4.5π x 10 ^-6 m² x 3 Ω / 150 m = 2.83 x 10 ^-7 Ω.m

Referenser

1. Resnick, r. 1992.Fysisk. Tredje upplagan utvidgades på spanska. Volym 2. Kontinentala redaktionella företag s.TILL. av C.V.
2. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14^th. Ed. Volym 2. 817-820.
3. Serway, R., Jewett, J. 2009. Fysik för vetenskap och teknik med modern fysik. Sjunde upplagan. Volym 2. Cengage Learning. 752-775.
4. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.
5. Sevilla universitet. Institutionen för tillämpad fysik III. Densitet och strömintensitet. Återhämtat sig från: oss.är.
6. Walker, J. 2008. Fysik. 4: e upplagan. Pearson.725-728