Kompletterande vinklar som är, beräkning, exempel, övningar

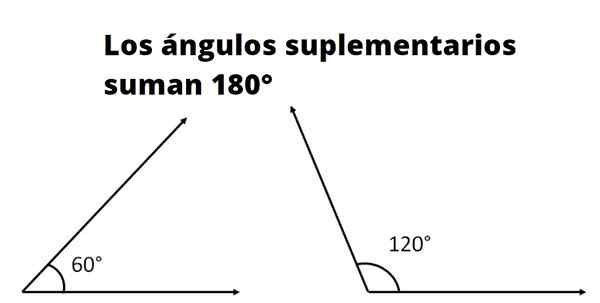
Två eller flera är kompletterande vinklar Om summan av dess åtgärder motsvarar måttet på en platt vinkel. Måttet på en platt vinkel, även kallad platt vinkel, i grader är 180º och i radianer är π.

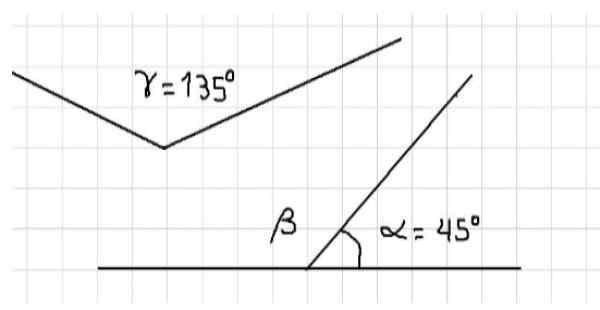
Till exempel finner vi att de tre inre vinklarna i en triangel är kompletterande, eftersom summan av dess åtgärder är 180º. Tre vinklar visas i figur 1. Från ovanstående följer det att a och ß är kompletterande, eftersom de är intilliggande och deras fulla summa en platt vinkel.

Figur 1: α och ß är kompletterande. α och y är kompletterande. Källa: f. Zapata.

Även i samma siffra finns vinklar a och y som också är kompletterande, eftersom summan av deras åtgärder är lika med omfattningen av en platt vinkel, det vill säga 180º. Det kan inte sägas att vinklarna ß och y är kompletterande eftersom de båda stöt vinklar är deras åtgärder större än 90º och därför överstiger dess summa 180º.

Källa: Lafer.com

Å andra sidan kan man säga att måttet på vinkeln ß är lika med måttet på vinkeln γ, eftersom om ß är kompletterande av a och y är kompletterande av a, sedan ß = y = 135º.

[TOC]

Exempel

I följande exempel uppmanas att hitta de okända vinklarna, indikerade med förhör i figur 2. De sträcker sig från de enklaste exemplen till några lite mer detaljerade än läsaren borde vara mer försiktig.

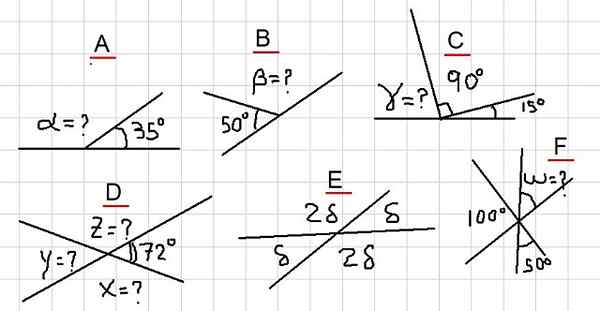figur 2. Olika exempel på kompletterande vinklar. Källa: f. Zapata.

Exempel a

I figuren har vi att de angränsande vinklarna α och 35º tillför en platt vinkel. Det vill säga α + 35º = 180º och därför uppfylls det att: α = 180º- 35º = 145º.

Exempel B

Eftersom ß är kompletterande med vinkeln på 50º följer det att β = 180º - 50º = 130º.

Kan tjäna dig: Vilka är elementen i liknelsen? (Delar)

Exempel c

Från figur 2c märks följande summa: y + 90º + 15º = 180º. Det vill säga, γ är kompletterande med vinkel 105º = 90º + 15º. Då dras slutsatsen att: 

y = 180º- 105º = 75º

Exempel D

Eftersom x är kompletterande med 72º följer det att x = 180º - 72º = 108º. Dessutom är det kompletterande med x, sedan y = 180º - 108º = 72º.

Och slutligen z är kompletterande med 72º, därför z = 180º - 72º = 108º.

Exempel E

Vinklarna Δ och 2Δ är kompletterande, därför Δ + 2Δ = 180º. Vilket innebär att 3Δ = 180º, och detta i sin tur tillåter att skriva: Δ = 180º / 3 = 60º.

Exempel f

Om vi ​​kallar vinkeln mellan 100º och 50º, är det då nödvändigt att kompletteras till dem, eftersom det observeras att deras fulla summa är en platt vinkel.

Det följer att u = 150º. Eftersom du motsätter sig toppen till w, då w = u = 150º.

Övningar

Tre övningar föreslås nedan, i alla av dem måste värdet på vinklar A och B hittas i grader, så att förhållandena som visas i figur 3 är uppfyllda. Begreppet kompletterande vinklar används i upplösningen av dem alla.

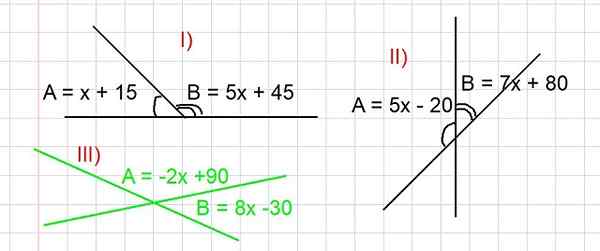Figur 3. Figur för att lösa övningar I, II och III på kompletterande vinklar. Alla vinklar uttrycks i grader. Källa: f. Zapata.

- Övning I

Bestäm värdena på vinklar a och b i del I) i figur 3.

Lösning

A och B är kompletterande, där A + B = 180 grader måste bytas ut, sedan ersätts uttrycket av A och B som en funktion av X, som den visas i bilden:

(x + 15) + (5x + 45) = 180

En första ordning linjär ekvation erhålls. För att lösa det kastas villkoren bort: Villkoren:

6 x + 60 = 180

Kan tjäna dig: riktiga siffror: historia, exempel, egenskaper, operationer

Att dela båda medlemmarna mellan 6 är:

x + 10 = 30

Och slutligen rensar, det följer att X är värt 20º.

Nu måste värdet på X bytas ut för att hitta de ordnade vinklarna. Därifrån måste du vinkla A: A = 20 +15 = 35º.

Och för sin del är vinkel B B = 5*20 + 45 = 145º.

- Övning II

Hitta värdena på vinklar a och b i del II) i figur 3.

Lösning

Eftersom A och B är kompletterande vinklar har A + B = 180 grader. Att ersätta uttrycket av A och B som en funktion av X som ges i del II) i figur 3 är:

(-2x + 90) + (8x - 30) = 180

Återigen erhålls en första gradsekvation, för vilken termerna måste vara bekvämt grupp:

6 x + 60 = 180

Att dela båda medlemmarna mellan 6 är:

x + 10 = 30

Där det följer att X är värt 20º.

Det vill säga att vinkeln a = -2*20 + 90 = 50 °. Medan vinkel B = 8*20-30 = 130.

- Övning III

Bestäm värdena på vinklar a och b i del III) i figur 3 (i grönt).

Lösning

Eftersom A och B är kompletterande vinklar har A + B = 180 grader. Uttrycket av A och B måste ersättas som en funktion av X som anges i figur 3, som du har:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Dela båda medlemmarna med 12 för att rensa värdet på X, du har:

x + 5 = 15

Slutligen har det konstaterats att X är värt 10 grader.

Fortsätt nu att ersätta för att hitta vinkel A: A = 5*10 -20 = 30 °. Och för vinkel B: B = 7*10 + 80 = 150º

Kan tjäna dig: vad är statistikområdet? (Med exempel)

Kompletterande vinklar i två paralleller klippta av en sekant

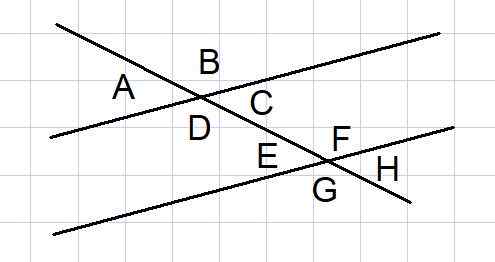Figur 4. Vinklar mellan två paralleller klippta av en sekant. Källa: f. Zapata.

Två parallella linjer klippta av en sekant är en vanlig geometrisk konstruktion i vissa problem. Bland sådana linjer bildas 8 vinklar som visas i figur 4.

Av dessa åtta vinklar är vissa par vinklar kompletterande, som vi listar nedan:

1. De yttre vinklarna till och B, och exteriörerna g och h
2. Interiörvinklarna D och C och interiörerna E och F
3. De yttre vinklarna A och G och den yttre B och H
4. De inre vinklarna d och e och de fångarna c och f

Genom fullständighet namnges också lika vinklar:

1. De interna växlingarna: d = f och c = e
2. De externa växlingarna: a = h och b = g
3. Motsvarande: a = e och c = h
4. Motsatserna med toppunkt a = c och e = h
5. Motsvarande: b = f och d = g
6. Motsatserna med toppunkt b = d och f = g

- Övning IV

Med hänvisning till figur 4, i vilken vinklarna visar mellan två parallella linjer skärning av en sekant, bestäm värdet på alla vinklar i radianer, och vet att vinkeln a = π/6 radianer.

Lösning

A och B är kompletterande yttre vinklar därför B = π - A = π - π/6 = 5π/6

A = e = c = h = π/6

B = f = d = g = 5π/6

Referenser

1. Baldor, J. TILL. 1973.Platt och rymdgeometri. Centralamerikansk kultur. 
2. Matematiska lagar och formler. Vinkelmätningssystem. Hämtad från: Ingemecanica.com.
3. Wentworth, g. Planetgeometri. Återhämtat sig från: Gutenberg.org.
4. Wikipedia. Kompletterande vinklar. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Transportband. Återhämtad från: är.Wikipedia.com
6. Zapata f. Goniometer: Historia, delar, operation. Hämtad från: Lifer.com