Kriterier Liknande trianglar

Vilka är Triangles likhetskriterier?

Trianglarnas likhetskriterier är reglerna som gör det möjligt att veta om två trianglar är liknande. Likheten mellan geometriska figurer, inklusive trianglar, kräver att siffrorna har på samma sätt, även om de inte nödvändigtvis har samma storlek eller samma orientering.

För att två trianglar ska vara liknande är det nödvändigt att: i) deras homologa sidor är proportionella och ii) de inre vinklarna för var och en har samma mått.

Figur 1. Två liknande trianglar: Även om de inte har samma storlek är deras sidor proportionella och deras inre vinklar har lika mått. Källa: f. Zapata.

Ett proportionellt förhållande eller proportion mellan två mängder A och B representeras av A/B -förhållandet, med B ≠ 0. För liknande trianglar är följande proportioner mellan deras sidor giltiga:

a/a '= b/b' = c/c '= r

Värdet på R kallas likhetsskäl.

Dessutom måste motsvarande inre vinklar vara av samma mått, därför: ∠A = ∠A '; ∠B = ∠B 'och ∠C = ∠C'. Enligt dessa förhållanden är Triangles likhetskriterier:

Kriterier 1: Två trianglar är liknande om de har två inre vinklar med lika mått. Om så är fallet, mäter den tredje vinkeln också samma, eftersom summan av de inre vinklarna i någon triangel är 180º:

α = α '; β = β '

Kriterier 2: Trianglarna är liknande om två homologa sidor är proportionella och vinkeln mellan dem är densamma:

a/a '= b/b'; α = α '

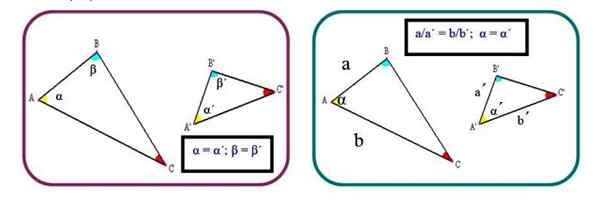figur 2. Två kriterier för att fastställa likheten mellan trianglar. Källa: f. Zapata.

Kriterier 3: De tre homologa sidorna är proportionella:

a/a '= b/b' = c/c '= r

Exempel

Trianglarnas likhet är mycket användbar för att beräkna höjder och avstånd som inte lätt kan mätas direkt. Genom några enkla beräkningar är det möjligt att ta reda på dessa längder genom att jämföra liknande trianglar.

Kan tjäna dig: grundläggande teorem av aritmetik: demonstration, applikationer, övningar

Höjd på kolumner, byggnader och träd

Det sägs att fadern till geometri i forntida Grekland, till exempel Miletus (625-547 till.C.), beräknade höjden på kolonnen i ett tempel utan behov av specialinstrument, helt enkelt jämföra längden på skuggan av sin sockerrör med kolonnens likhet och tillämpa trianglarnas likhet. Med samma metod lyckades han mäta höjden på Egyptens stora pyramid och därmed imponera på farao.

Avståndet till månen

Det finns ett enkelt experiment som görs för att beräkna avståndet mellan jorden och månen. Det kräver en valuta, lite självhäftande tejp och en vernier eller en examenregel. När månen är full är valutan fäst vid glaset i ett fönster och månen observeras med ett öga, beläget på ett sådant sätt att valutan täcker bara fullmånen.

När detta händer är orsaken mellan diametern på valutan och avståndet mellan ögat och valutan detsamma som det finns mellan månens diameter och avståndet mellan ögat och månen:

Valutadiameter/distansvaluta = Måndiameter/avstånd till månen

Anledningen är ungefär 1/110. Vilket innebär att avståndet till månen är 110 gånger diametern på detta.

För närvarande uppskattas månens radie 1737.1 km, så dess diameter är 3474.2 km. Genom att ersätta detta värde i förhållandet:

Avstånd till månen = måndiameter ÷ (valutadiameter/avstånd till valutan)

Erhålles:

Avstånd till månen = 3474.2 km ÷ (1/110) = 382.162 km

Det kan tjäna dig: hepagonalt prisma

Mycket nära värdet som fastställts av 384 astronomer.000 km.

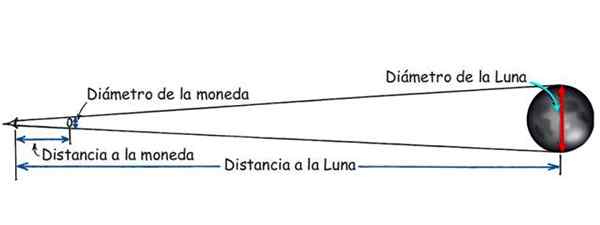Figur 3. Avståndet till månen kan vara känt tack vare likheten mellan trianglar. Källa: Modifierad Hewitt, P. Konceptuell fysik.

Avstånd mellan ett fartyg och stranden

För att mäta avståndet mellan fartyget och stranden är insatser fast på stranden i punkter A, B, C och Q. ABC- och PCQ -trianglar liknar med kriterier 1, eftersom de har två lika vinklar: de två vinklarna ∠C = α som motsätter sig av toppen och de två raka vinklarna lika med 90º: ∠B = ∠Q.

Två trianglar som finns på detta sätt sägs vara i Thales position Och de är alltid lika. Trianglar identifieras i Thales position för att ha en gemensam vinkel och motsatta sidor i den vinkeln är parallella.

I nästa avsnitt finns en övning med numeriska värden.

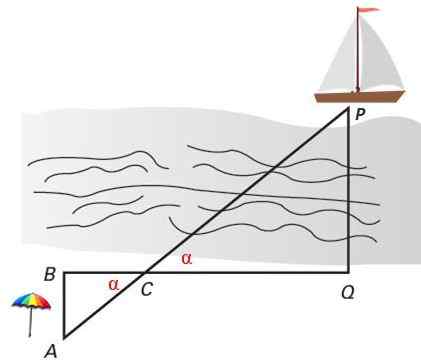Figur 4. Två liknande trianglar i Thales -läge tjänar till att beräkna det vinkelräta avståndet till ett fartyg till stranden. Källa: f. Zapata.

Löst övningar

Övning 1

Du vill ta reda på hur långt segelbåten är förankrad i föregående figur, från en punkt som ligger på stranden av stranden, för vilka insatser är spikade i punkter A, B, C och Q, och bestämmer därmed triangeln ABC, som liknar PCQ, men vars sidor är lättare att mäta.

Beräkna det vinkelräta avståndet PQ mellan fartyget och stranden, genom likhet mellan trianglar, om de avstånd som finns tillgängliga är:

Ab = 12 m

BC = 16 m

QC = 60 m

Lösning

Proportionerna mellan homologa sidor är:

Ab/qp = bc/cq = 16 m/60 m = 0.267

Därför 0.267 är orsaken till likhet:

AB/QP = 0.267

Qp = ab / 0.267 = 12 m / 0.267 = 44.9 m

Övning 2

I följande triangel: hur mycket mäter annonssegmentet?

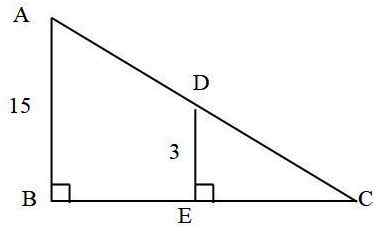
Det är känt att:

• AC = 25 cm
• Ab = 15 cm
• De = 3 cm

Kan tjäna dig: multiplar av 2: vad är och förklaring

Lösning

Trianglarna är liknande, eftersom de delar en vinkel som är ∠C och sidorna på och ab är parallella. Likhetsförhållandet beräknas av:

R = AB / DE = 15 cm / 3 cm = 5

Och även genom:

R = AC / DC

Därför DC = AC / R = 25 cm / 5 = 5 cm

Eftersom:

AC = AD + DC

Det följer att AD = AC - DC = 25 cm - 5 cm = 20 cm

Övning 3

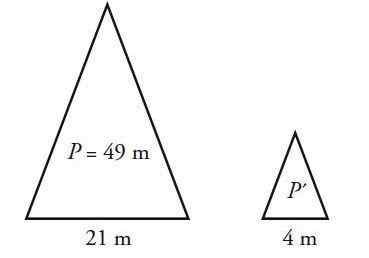
En isosceles triangel har en omkrets på 49 cm och en bas på 21 cm. Beräkna omkretsen av en triangel som liknar detta, men vars bas mäter 4 cm.

Lösning

Isosceles triangel har två lika sidor, annorlunda än bas B. Låt ℓ måtten på sidorna och P omkretsen, som består av summan av de tre sidorna. För den största triangeln:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Nu höjs andelen mellan sidorna av trianglarna, de i den lilla triangeln symboliseras med premier:

B/ b '= ℓ/ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

Omkretsen av den lilla triangeln kommer att vara:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Hewitt, Paul. 2012. Konceptuell fysisk vetenskap. Femte. Ed. Pearson.
3. Clemens, s. Geometri med applikationer. Addison Wesley.
4. Ibáñez, s. 2010. Matematik III. Cengage Learning.
5. Jiménez, r. Matematik II: Geometri och trigonometri. 2: a. Utgåva. Pearson.
6. Stewart, J. 2007. Förkalkning. Femte. Utgåva. Cengage Learning.
7. Vicmat. Samos Aristarco: Solsystem mäter. Återhämtat sig från: vicmat.com