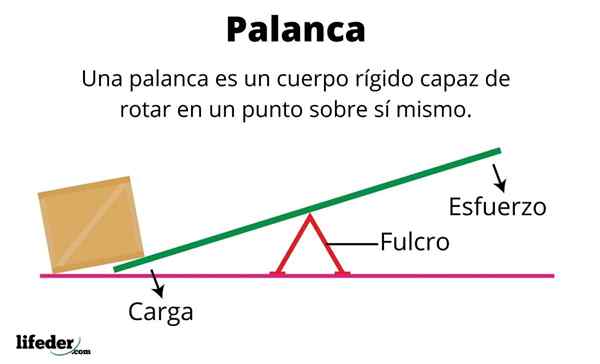
Stel kropp

Vad är en styv kropp?

En styv kropp är ett materiellt objekt vars partiklar alltid förblir i samma relativa positioner. Därför är det ett objekt som inte är deformerat, en kvalitet som tillskrivs de intensiva sammanhållningskrafterna som håller partiklarna på plats.

Egentligen tenderar partiklarna i alla kroppar som är föremål för yttre krafter att vibrera eller röra sig, så objektet deformeras alltid i viss utsträckning, men dessa effekter är vanligtvis små.

När detta är fallet kan det antas att kroppen är styv och har en mycket bra inställning till dess beteende, även om det är en idealisering.

Styva kroppstyper

Du kan skilja två typer av styva kroppar:

• De vars partiklar kommer i diskreta mängder, det vill säga de kan räkna. Till exempel kan två metallfärer kopplade av en tunn och lätt stång betraktas som en unik enhet. Om stången är tillräckligt styv för att inte böja, betraktas systemet som en styv kropp.
• De som är kontinuerliga, vilket innebär att partiklarna som gör dem är oskiljbara. Vardagliga och naturobjekt är bra exempel: stenar, möbler och andra, såväl som landet och andra himmelstenar steniga.

Styv kroppsrörelse och dynamik

Liksom föremål som betraktas som partiklar kan styva kroppar överföras, rotera och ha en mer allmän rörelse, kombinera översättning och rotation.

För att studera översättningen är det inte nödvändigt.

Dessa översättnings- och rotationsrörelser kan vara:

• Oberoende, som i fallet med planeterna, som har en rotationsrörelse runt deras axel (anses fixerad) och en annan översättning runt solen, men hastigheterna för var och en är inte relaterade.
• Trasigt skräp, om vinkelhastigheten och översättningshastigheten för massans centrum är relaterade. I detta fall är rotationsaxeln mobil, som i fallet med cylindern som går ner skjutning utan att glida av en lutande sluttning.

Det kan tjäna dig: första lagen om termodynamik: formler, ekvationer, exempel

Dynamiken i styv solid

Följande storlekar är relevanta i dynamiken i styvt fasta ämnen:

Masscentrum

Massens centrum är den punkt där hela kroppens massa anses vara koncentrerad. Om det är en homogen och symmetrisk kropp, som en sfär, sammanfaller mitten av massan med det geometriska centrumet.

Tröghetsmomentet

Denna skalära storlek är värdet av rotationens tröghet eller motstånd som motsätter sig ett objekt för att rotera runt en viss axel. Det beror helt på objektets och dess massa geometri och därför är det i vissa fall lättare att vända vissa axlar än på andra.

För kroppar med väl definierade geometriska former finns det bord med tröghetsmoment med avseende på symmetriens axlar, till exempel den som passerar genom masscentret. Med denna information och teorems relaterade till tröghetsmomentet kan ögonblicken med avseende på andra axlar lätt beräknas.

Krafter och vridmoment eller vridmoment

Krafter måste flytta en kropp. Om det styva solida masscentret rör sig är rörelsekvationen enligt Newtons andra lag:

F_Netto = M ∙till_centimeter

Var:

-Nettokraften är F_Netto

-M är massan

-Masscentrets acceleration är till_centimeter

Men inte alla tillämpade krafter får objektet att bryta. För att göra detta behövs vridmomentet eller vridmomentet, vilket säger hur effektivt det är en kraftverk av en kraft. Det definieras som vektorprodukten mellan positionsvektorn r När det gäller en viss punkt och kraft F i fråga. Det betecknas av det grekiska brevet τ (I djärv bokstav är det också en vektor):

Kan tjäna dig: elliptisk rörelse

τ = r × F

I det internationella systemet är vridmomentenheten N⋅m (Newton per meter).

I många fall beskrivs rotationsrörelsen runt en axel som passerar genom masscentrumet av en analog ekvation med Newtons andra lag:

Där abonnemanget "z" hänvisar till rotationsaxeln som passerar genom en symmetrixaxel, fixerad eller rörlig, men utan att ändra riktning, och_centimeter Det är tröghetsmomentet med avseende på massan och α_z Det är kroppens vinkelacceleration. Sommaren täcker alla yttre stunder runt z -axeln.

Kinetisk energi av ett styvt fast ämne

Rörelsen av en styv kropp beskrivs genom översättningar av massans centrum och rotationer runt den punkten, därför har dess kinetiska energi båda bidrag.

Låt K kroppens kinetiska energi, v_centimeter Masscentrumets hastighet, m massans massa och_centimeter Dess tröghetsmoment med avseende på massans centrum och Ω vinkelhastigheten. Det kan demonstreras att kinetisk energi är:

K = ½ mV_centimeter² + ½ i_centimeter Ω²

Det observeras att den andra termen till höger är rotationsanalogen för vänstern till vänster. Där spelar tröghetsmomentet samma roll som massan, medan vinkelhastigheten har samma roll som den linjära hastigheten.

Exempel i vardagen

Fysisk pendel

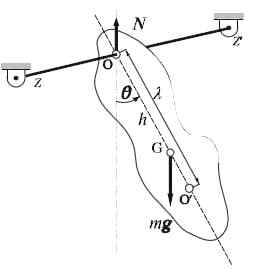Fysisk pendel

Den fysiska pendeln eller den riktiga pendeln är mycket lätt att bygga: den består av ett styvt fast ämne som en stav eller stång, som svänger fritt runt en horisontell axel. Rotationsaxeln passerar inte föremålets centrum och detta kan i princip ha någon form.

Kan tjäna dig: Motståndstermometer: Egenskaper, drift, användningar

Denna pendel skiljer sig från den enkla pendeln, eftersom det i det senare anses att massan som komponerar den är punktlig.

Cykelhjul

Cykelhjul

Ett annat välkänt styvt kroppsexempel är cykelhjulet, vars axel passerar genom massans centrum, som korsar hjulets centrum. Så länge de inte lutar sig åt sidan eller vänder, gäller ekvationerna i den beskrivna dynamiken för att beskriva din rörelse.

En bowlingboll

Ett bra exempel på en styv kropp är bowlingbollen

Den styva solida modellen anpassar sig mycket bra för att beskriva bowlingbollens rörelse på banan eller när den rullar utan att glida ner returrampen.

Yoyo

Yoyo är en populär leksak som kan modelleras som en styv kropp

Denna populära leksak är gjord med en trä- eller plastcylinder och ett rep överväldigat i en plats som omger den.

Cylindern kan modelleras som en styv kropp där spänningen i strängen ger vridmomentet för rotationen, medan vikten (appliceras på masscentrum) och spänningen är ansvarig för den vertikala accelerationen av massans centrum.

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill. 
2. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
3.  Katz, D. 2013. Fysik för forskare och ingenjörer. Stiftelser och anslutningar. Cengage Learning.
4. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1. Pearson.
5. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.