Regelbunden, oregelbunden decagon, egenskaper, exempel

han decagon Det är en platt figur med en polygonformad av 10 sidor och 10 vertikaler eller tips. Avkagnarna kan vara regelbundna eller oregelbundna, i det första fallet har alla sidor och inre vinklar samma mått, medan i den andra sidorna och/eller vinklarna skiljer sig från varandra från varandra.

Figur 1 visar exempel på dekagoner av varje typ och som vi kan se är den vanliga decagon mycket symmetrisk.

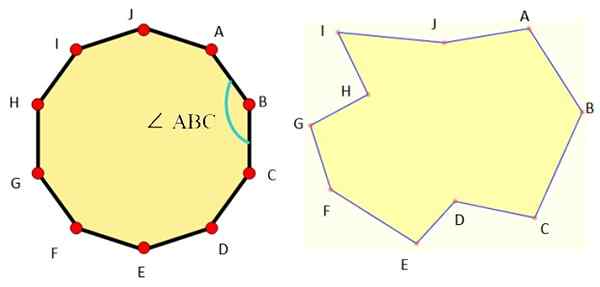Figur 1. Till vänster en vanlig decagon och till höger en oregelbunden decagon. Källa: Wikimedia Commons/F. Zapata/MathPenref.

De grundläggande elementen i alla decagon är:

-Sidor, linjesegmenten som när du går med i decagon.

-Vertikaler eller punkter mellan varje på varandra följande sida.

-Inre och yttre vinklar mellan angränsande sidor.

-Diagonaler, segment som förenar två icke -konsekutiva hörn.

Herren kallas med stora bokstäver, som visas i figur 1, där de första bokstäverna i alfabetet användes, men alla bokstav kan användas.

Sidorna symboliseras med de två bokstäverna i vertikalerna bland vilka till exempel AB -sidan är den mellan topparna A och B. På samma sätt görs det med diagonalerna, så vi har diagonalen AF, som går med punkterna A och F.

För vinklar använder vi denna symbol: ∠, liknande en lutande L. Till exempel är vinkeln ∠ ABC en vars toppunkt är B och vars sidor är AB- och BC -segmenten.

[TOC]

Ordinarie decagon

I den vanliga decagon har alla sidor samma mått, liksom inre vinklar. Därför sägs det vara liksidig (lika sidor) och likvinklig (Lika vinklar). Det är en mycket symmetrisk figur

Inre vinklar i en vanlig decagon

För att hitta måtten på de inre vinklarna på en vanlig polygon, inklusive den vanliga decagon, används följande formel:

Var:

-Jag är måtten på vinkeln i grader.

-n är antalet sidor av polygonen. När det gäller decagon n = 10.

Kan tjäna dig: Hepagon

Ersätter n = 10 I den föregående formeln får vi följande:

Nu sägs det att en polygon är konvex Om dess vinkelåtgärder är mindre än 180º, annars är polygonen konkav. Liksom alla inre vinkel i den vanliga decagon mäter 144º och är mindre än 180º, är det en konvex polygon.

Summan av inre vinklar

Summan av måtten på de inre vinklarna för någon polygon är i grader:

S = (n-2) x 180º; n är alltid större än 2

I denna formel måste vi:

-S är summan av måtten på de inre vinklarna.

-n är antalet sidor. För decagon n = 10

Tillämpa formeln för n = 10 resultat:

S = (10 - 2) x 180º = 1440º

Yttre vinklar 

En yttre vinkel bildas mellan ena sidan och förlängningen av den angränsande sidan, låt oss se:

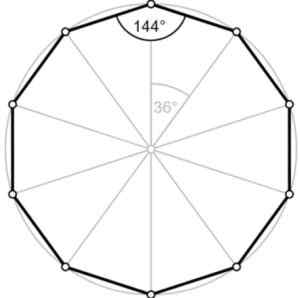
figur 2.- Den yttre vinkeln för den vanliga decagon mäter 36º. Fontän. Wikimedia commons/f. Zapata.

Vinkeln ∠ ABC plus den yttre vinkeln lägger till 180º, det vill säga de är Tilläggs-. Därför är den yttre vinkeln lika med 180º-144º = 36º, som vi ser i figuren.

Antal diagonaler

Som nämnts tidigare är diagonalerna de segment som förenar icke -konsekutiva toppar. Hur många diagonaler kan vi spåra i en decagon? När antalet toppar är litet kan de enkelt räknas, men när det antalet ökar kan du förlora kontot.

Lyckligtvis finns det en formel att veta antalet diagonaler som en polygon har n sidor:

För decagon ersätter vi n = 10 och får:

D = 10 x (10 - 3) /2 = 35

I den vanliga decagon skärs alla diagonaler vid en punkt, vilket är mitten av figuren:

Figur 3. Vinklar och diagonaler i den vanliga decagon. Källa: Wikimedia Commons.

Centrum

Mitten av en polygon definieras som den likvärdiga punkten för alla vertex. I föregående siffra sammanfaller mitten med korsningspunkten för alla diagonaler.

Omkrets

Om den vanliga decagon har sida A är dess omkrets P summan av alla sidor:

Kan tjäna dig: 90 delare: vad är och förklaring

P = 10.till

Område

Att känna till längden till På sidan beräknas det vanliga decagonområdet av:

En ungefärlig formel för området är:

Och ett tredje alternativ för att hitta området är i längden på apotem l_TILL. Detta är det segment som går med i mittpunkten på ena sidan med mitten av polygonen.

I detta fall kan området beräknas med formeln:

Oregelbunden decagon

Den oregelbundna decagon är inte liksidig eller jämlik, och i allmänhet saknar den symmetrin för den vanliga figuren, även om vissa dekagoner kan ha symmetrixel axel.

De kan också vara konvexa eller konkava, om det finns inre vinklar större än 180º.

Den oregelbundna decagon i figur 1 är konkav, eftersom några av dess inre vinklar är större än 180º. Det är uppenbart att det finns många kombinationer av vinklar och sidor som ger upphov till en oregelbunden decagon.

I alla fall är det uppfyllt att:

-De inre vinklarna på en oregelbunden decagon lägger också till 1440º.

-Den har också 35 diagonaler.

Område med en oregelbunden decagon av Gauss -determinanter

I allmänhet finns det ingen unik formel för att hitta området för en oregelbunden polygon, eftersom sidorna och vinklarna är olika. Du kan dock hitta att veta koordinaterna för vertikalerna och beräkna Gauss determinanter:

-Låt oss ringa (x_n , och_n ) till koordinaterna för vertikalerna, med n varierande från 1 till 10.

-Du kan börja från valfritt toppunkt, till vilka koordinater kommer att tilldelas (x x₁, och₁ ). Nu måste du ersätta värdena på varje koordinat i denna formel:

Där determinanter är just operationerna mellan parentes.

-Det är viktigt att notera att den sista determinanten involverar det första toppunktet tillsammans med det sista. För decagon skulle det vara så här:

(x₁₀och₁ - x₁och₁₀)

Kan tjäna dig: Lagrange interpolation

Viktig: Staplarna är de av absolut värde och betyder att det slutliga resultatet alltid är med ett positivt tecken.

Förfarandet kan vara mödosamt när figuren har många vertikaler, i fallet med decagon finns det 10 operationer, så det är tillrådligt att skapa en tabell eller en lista.

Träning löst

Beräkna det oregelbundna decagon -området som visas i figuren. Koordinaterna för topparna är a, b, c ... j, vars värden visas till vänster.

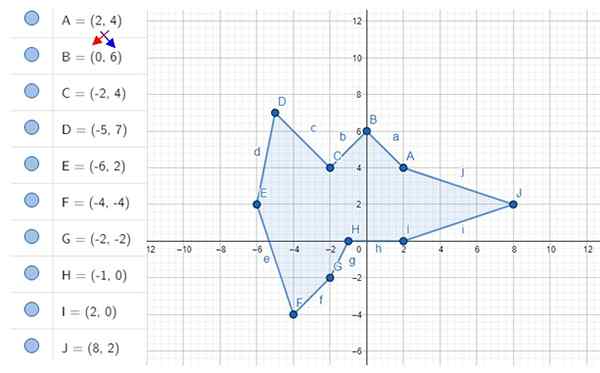Figur 4. Oregelbunden decagon och dess vertikaler. Källa: f. Zapata med geogebra.

Lösning

-Vi gör var och en av de tio operationerna:

• 2 × 6 - 4 × 0 = 12 - 0 = 12
• 0 × 4 - 6 × (-2) = 0 + 12 = 12
• (-2) × 7- 4 × (-5) = -14 + 20 = 6
• (-5) × 2 -7 × (-6) = -10 + 42 = 32
• (-6) × (-4) -2 × (-4) = 24 + 8 = 32
• (-4) × (-2)-(-4) × (-2) = 8-8 = 0
• (-2) × 0-(-2) × (-1) = 0 -2
• (-1) × 0 - 0 × (2) = 0 - 0 = 0
• 2 × 2 - 0 × 8 = 4 - 0 = 4
• 8 × 4 -2 × 2 = 32 - 4 = 28

-Vi lägger till resultaten:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Ett positivt resultat erhålls även utan staplarna med absolut värde, men om det är negativt ändras samma.

-Det föregående resultatet är dividerat med 2 och det är området för polygon:

A = 124/2 = 62

Decangonegenskaper

Nedan är sammanfattningen av de allmänna egenskaperna för en decagon, vare sig det är regelbundet eller oregelbundet:

-Har 10 sidor och 10 vertikaler.

-Summan av inre vinklar är 1440º.

-Det finns 35 diagonaler.

-Omkretsen är summan av alla sidor.

-Du kan skapa trianglar inuti en polygonritningssegment från en topp till alla andra. I en decagon är det möjligt att rita 8 trianglar på detta sätt, som visas nedan:

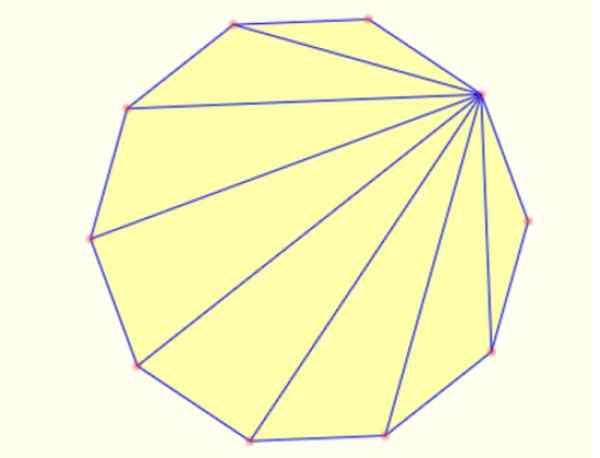Figur 5. Interna trianglar i en regelbunden decagon. Källa: MathPenref.

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Decagon.com. Decagon. Återhämtat sig från: Decagon.com
3. Matematik öppen referens. Decagon. Återhämtat sig från: MathPenref.com.
4. Sangaku matematik. Element i en polygon och dess klassificering. Återhämtat sig från: Sangakoo.com.
5. Wikipedia. Decagon. Återhämtad från: är.Wikipedia.com.